今回は私が使っているデジタルノギス(安物の中華製)の電池が切れて使えなくなったので電池の交換をして行きたいと思います。
それに加えてノギスを見ていたら計測器具の計測誤差の考え方の基本、計測工学の基本の一つであるアッべの原理を思い出しました。
折角なのでノギスの電池交換のついでにノギスが構造的に持つ計測誤差(内容的にこっちがメイン)を説明して行きたいと思います。
なので今回のメインの内容は機械系の大学生、エンジニアに向いているかも知れません(計測工学の単位取得のテストに絶対に出題される)。
まずはノギスの電池を交換します。
デジタルノギスの電池交換
使っているノギスは下の写真です。

安い割にそこそこ精度が良いので重宝しています(精度確認は後述)。
・デジタルノギス
安い割にそこそこの正確さです。ただし大きめ
電池が切れて使えないので交換して行きます。
ちなみに電池は初期から内臓のテスト電池と別に電池が付属しています。初期のテスト電池でもかなり長持ちしました。
電池ボックスを開けます。

写真の蓋はかなり硬いのですが頑張って開けて付属の電池と交換します。

これで復活したので試しに6mmのBB弾を測定してみました。

これが正確かどうかがわからないので同じ弾を自分のマイクロメーターで測定してみます。

マイクロメーターだと5.931mmなのでノギスの割に正確でした(およそ0.01mm差)。
構造的にマイクロメーターのが正確なのでこのデジタルノギスは0.01mmズレていることになります。
ではダメなノギスかというとそうではなくデジタル、アナログに関わらず構造的(論理的)にノギスは誤差が大きく私の感覚だと当てにできる精度は0.05mmが限界だと思います(マイクロメーターは0.005mm)。
なのでデジタルノギスの利点でもあり欠点にもなることが分かりやすく0.01mm単位で数字が出ますが、構造的に当てにできる精度は0.05mmになります(正確に使う場合は必ず0.00mm,0.05mm刻みに脳内で変換する)。
また構造と行ってもマイクロメーターは精密な送りネジを使っている、ノギスはガタが大きいとかの物理的な要因ではなく論理的な測定方法の違いによって誤差が大きく異なります。
おそらく多くの方が感覚的にノギスよりマイクロメーターのが精度が高いのを知っていると思いますが、この記事ではなぜ精度に差が出るのかを理論で明確にしてみます。
では“なぜノギスは論理的に誤差が大きいのか“を考えて行きます。
ノギスの 計測誤差を求める。
ここで折角なのでノギスの英語キャリパー(Caliper)、または副尺:バーニア(Vernier)を覚えましょう(マジでテストに出やすい)。
アナログの一般的なノギスの写真です。

アナログノギスの各部名称、使い方はここでは省きます(要望があれば書きます、工学系の学生は初等実験のテストで必ず出題されます)。
次にノギスである物体を測定した状態を描いてみます。
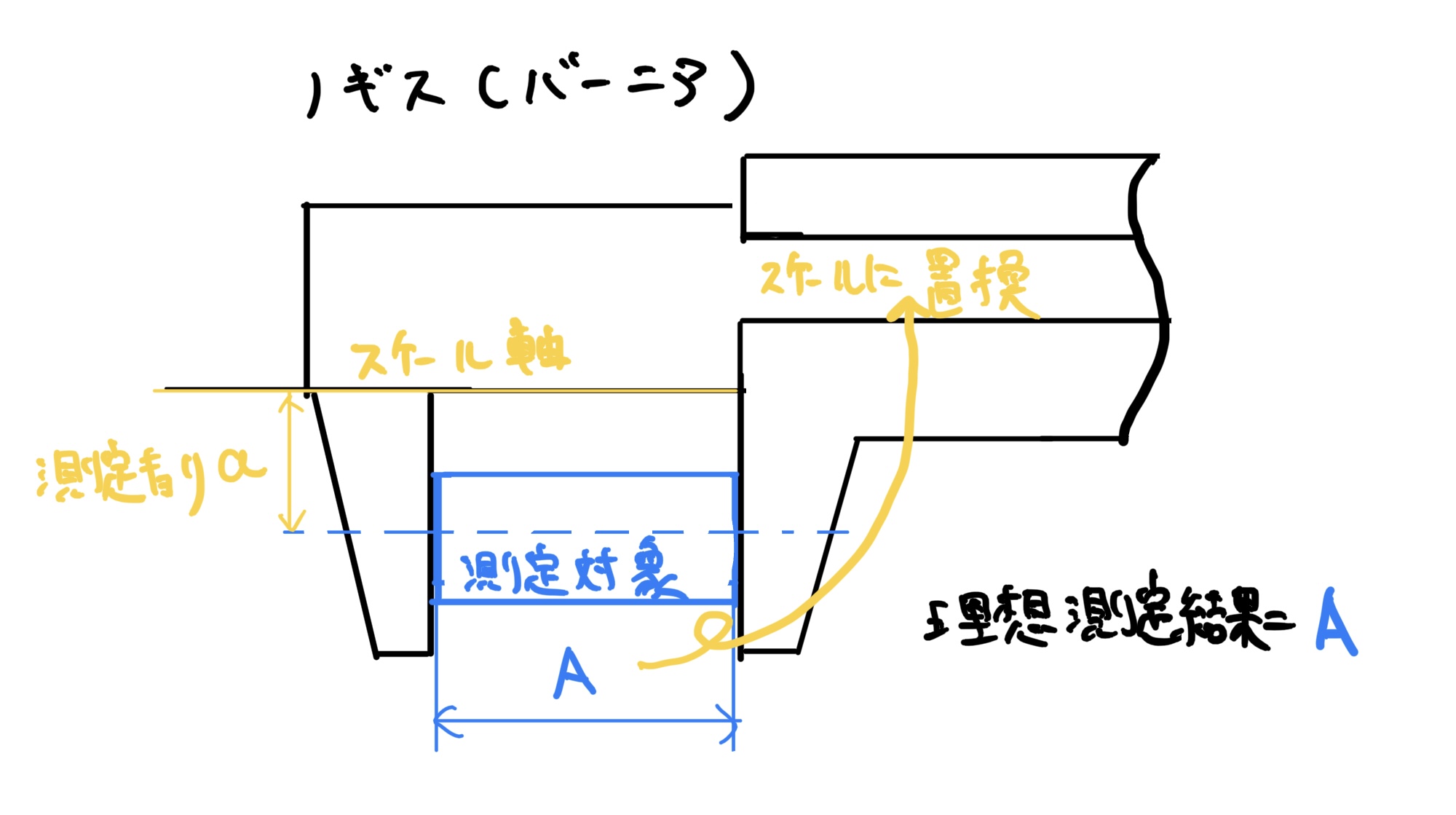
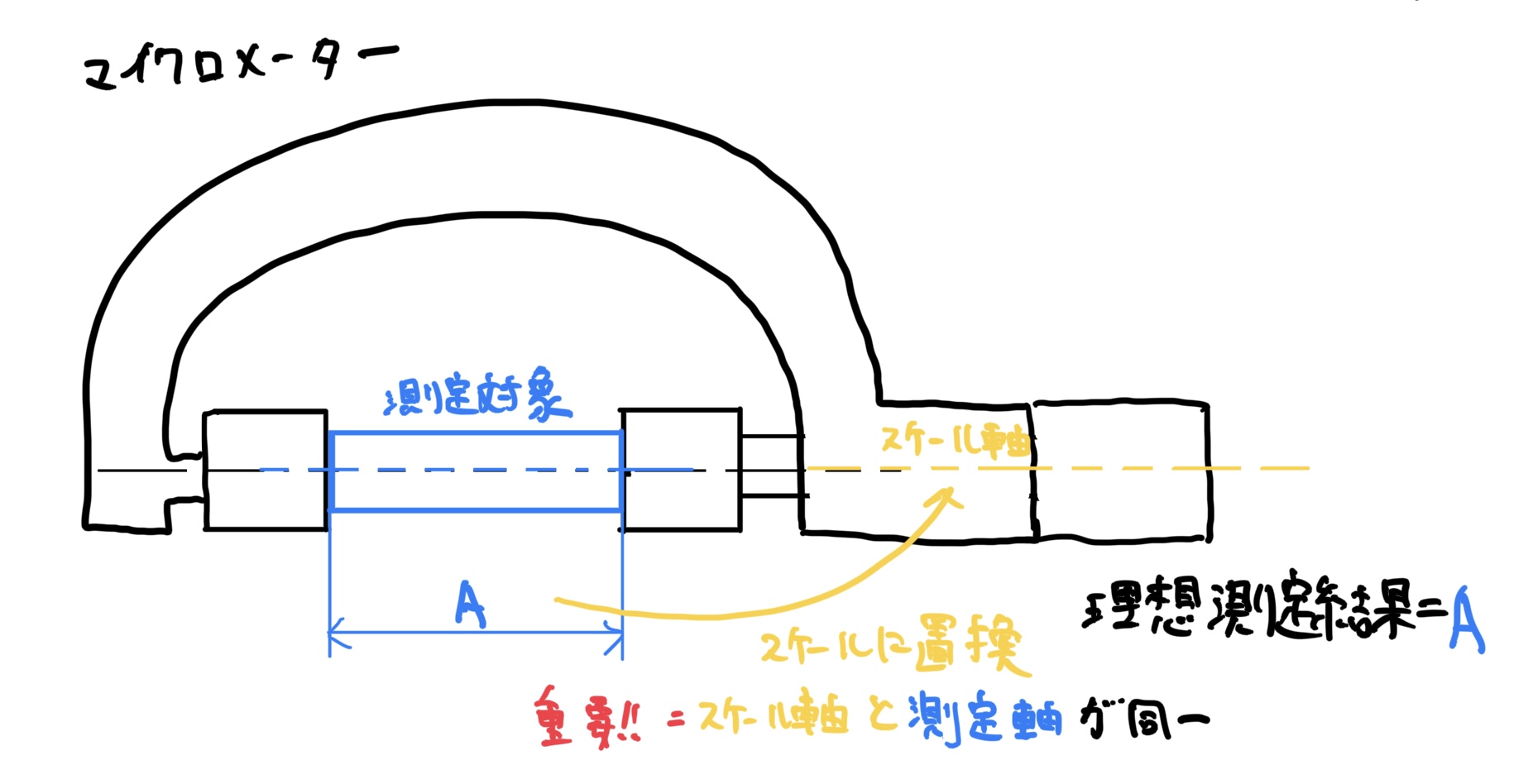
ここで主尺(メインの目盛り)をスケール軸と定義し軸から測定対象中心までの距離をaと定義します。
理想的(完璧)なノギスであれば絵の通り測定対象の長さAが測定できるはずです。
しかしながら実際にはガタが発生するので理想通りには計測できません。
次に複数存在するガタ、ズレの中で測定誤差が最も大きくなるガタを考えます。
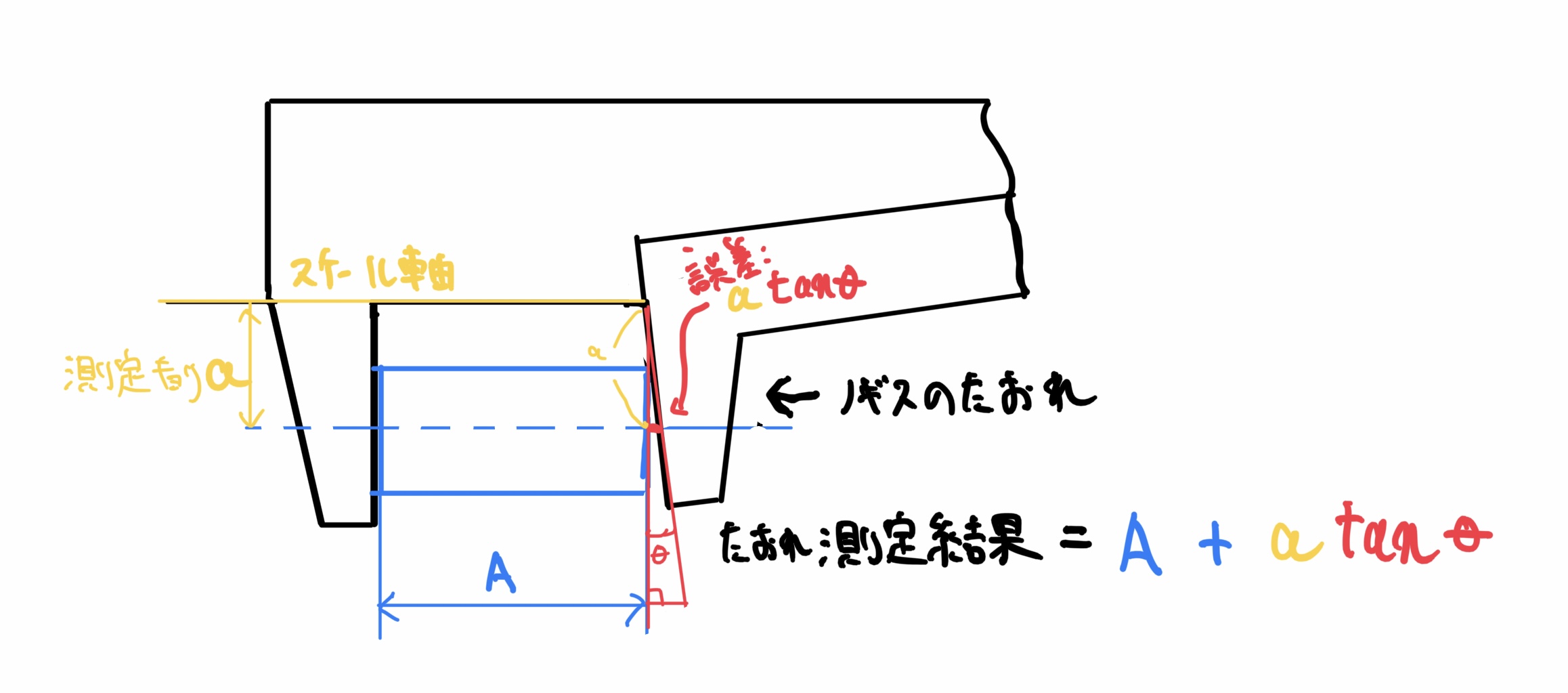
測定に最も影響を与えるのは測定部の倒れ(倒れ角をθと定義)になります。
ここで倒れ角θ、測定距離aを利用して測定結果を式にすると次のようになります(単純な三角関数、図形問題)。
$$ 倒れ測定結果=A+a\times tanθ $$
次に発生した誤差を求めるのは単純に理想的な測定結果から倒れ測定結果を引けば求められます(測定誤差をε:イプシロンとする)。
$$ 測定誤差ε=理想測定結果ー倒れ測定結果=a\times tanθ $$
になります。
式だけだと誤差のイメージが湧かないと思うので横軸をθ、縦軸を測定誤差εのグラフにします。
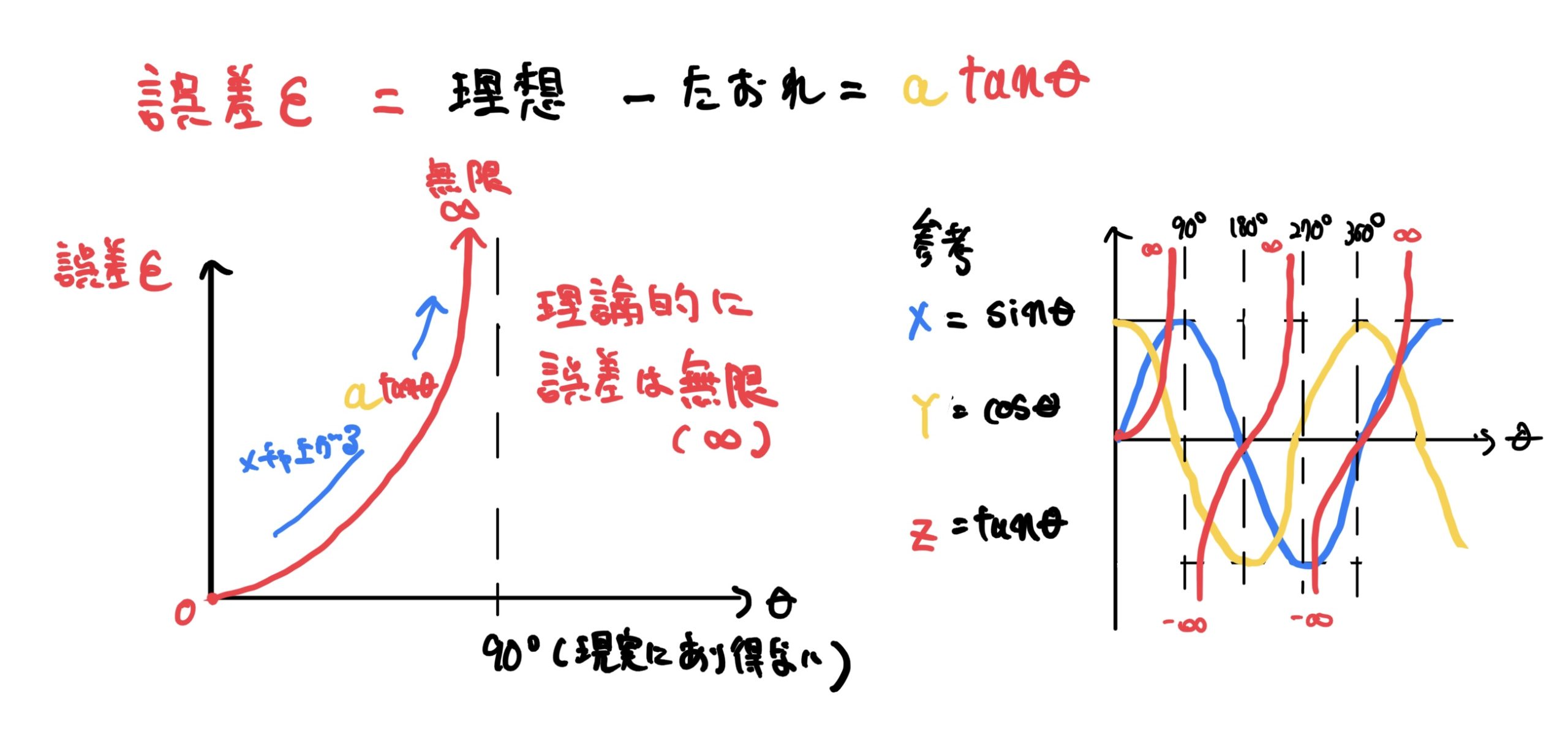
グラフの通り誤差はtanなので倒れ角θが増加すれば誤差も急激に増加する、極端に考えると倒れ角が90°(現実にも論理構造にも無い)の誤差は無限(∞)になります。
ここまで多くの方が“実際の倒れ角θはかなり小さいので誤差も大したことがないだろう“と考えると思います。
なので次にθがかなり小さい(極小)時の誤差の大きさを詳細に考えてみます(θが0°付近)。
式がtanのままでは角度θが極小の時の変化が分かりにくいのでtanをマクローリン展開します(マクローリン展開の概略は後述するので”ここではそういうものか”と考えて下さい)。
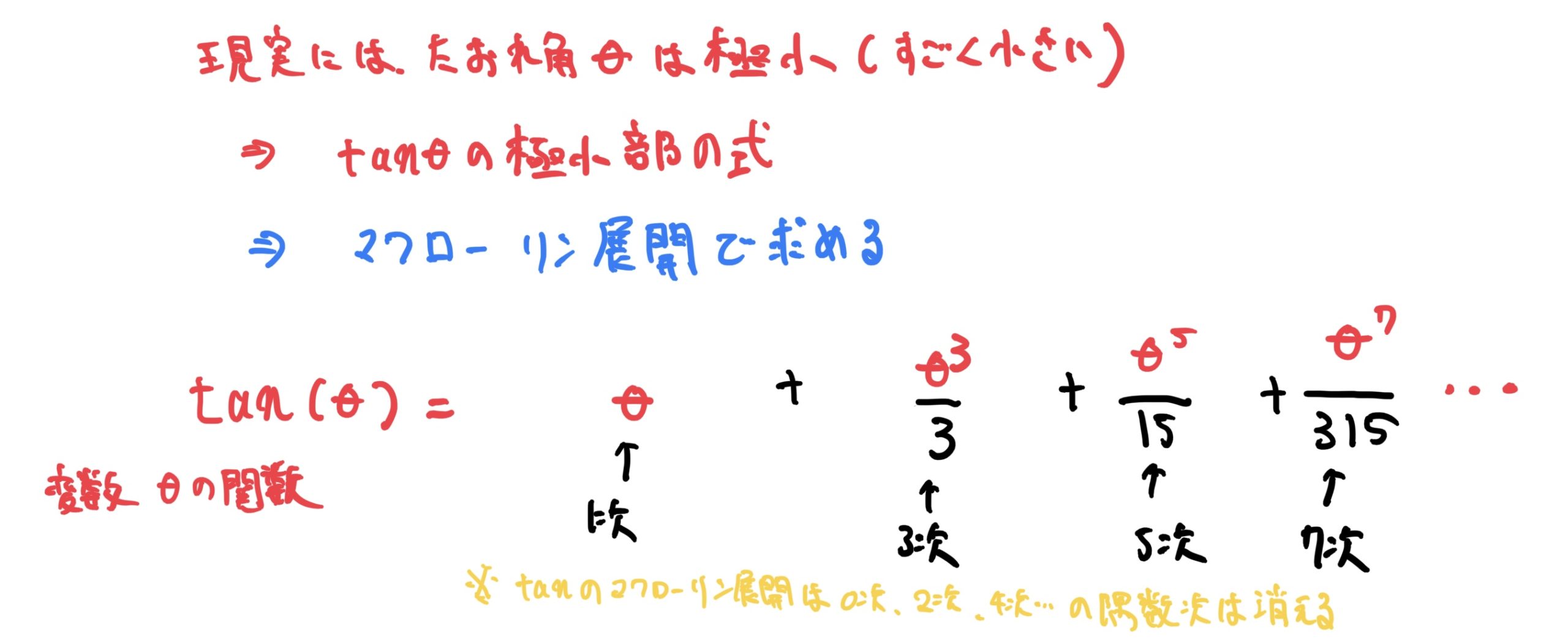
ここで展開した全ての項を使うとややこしくなるので3次成分$(θ^3)$までを使います(工学では基本的に2〜3次までで十分とする)。
また実際には展開した式ではθは角度(°)ではなくラジアン(radian、弧度法、角度180°=Π)にして計算します。
tanを展開式の3次の項までと交換して誤差εを求めます。
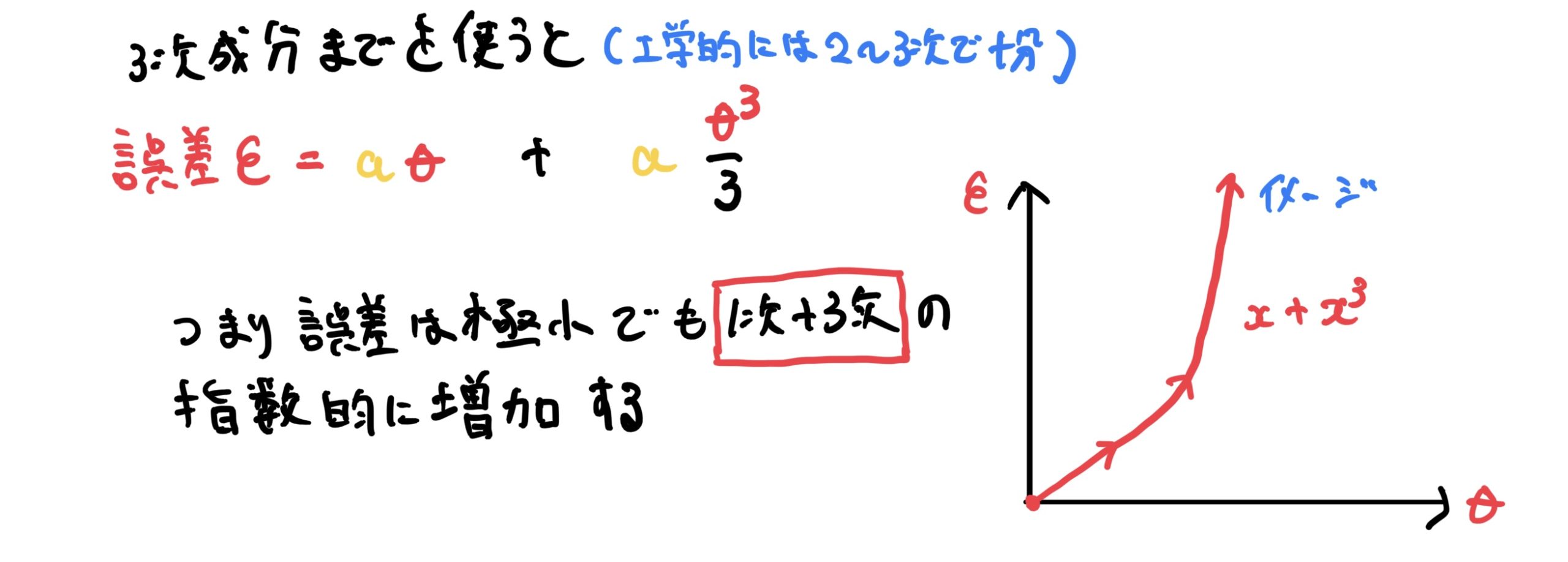
つまりノギスにおける計測誤差εは倒れ角θの1次、3次に比例して大きくなるので相当な大きさであることがイメージできると思います。
これがノギスの計測方法が持つ論理的な誤差の大きさになります。
実際のノギスも倒れかくに注意して選ぶと正確なノギスが手に入ります。なのでホームセンター等でノギスを買うときは同じ種類でもいくつか倒れを確認して買うと得します(人間の感覚の鋭さはバカにできない)。
次にマイクロメーターと行きたいところですがマクローリン展開の超簡単な概要を補足します(数学の先生に怒られそうな内容)。
マクローリン展開のイメージ、概要
まずは中学、高校で習った関数のおさらいです。関数は簡単に言うと変数同士(xとかy)の関係性を表しています。
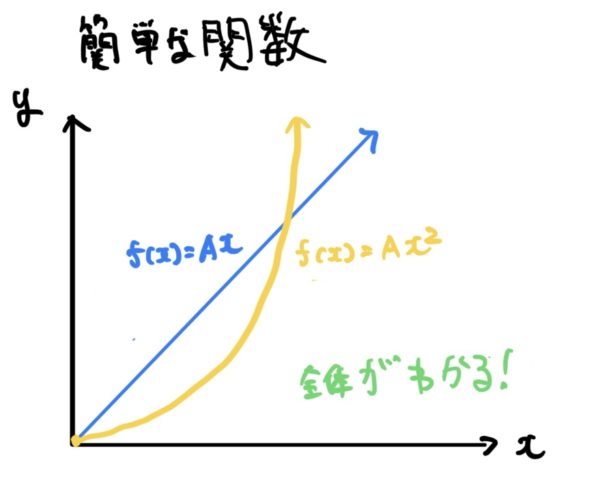
なんとなく思い出して欲しいのですが上のグラフだと
$$ y=f(x)=Ax、 つまりxが1になるとyがAになる、xが2ならyは2A $$
$$ y=f(x)=Ax^2 、 つまりxが1ならyはAになる、xが2ならyは4A $$
です。
このような簡単な関数であれば式も値も割と簡単にわかります。
しかし超複雑な関数(自然のほとんどは複雑)な関数はそう簡単にはわかりません。
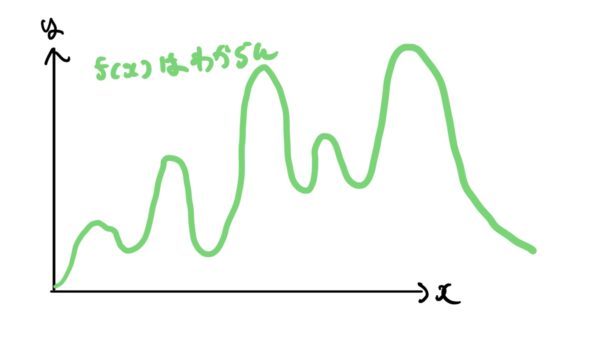
複雑すぎて超難しいから関数の解明を諦めてしまうのはもったないので人類の知恵の一つをここで使います。
関数の全体が難しすぎてわからないのは仕方がないので自分が知りたい範囲(特定の小さな範囲)を取り出して考えます。
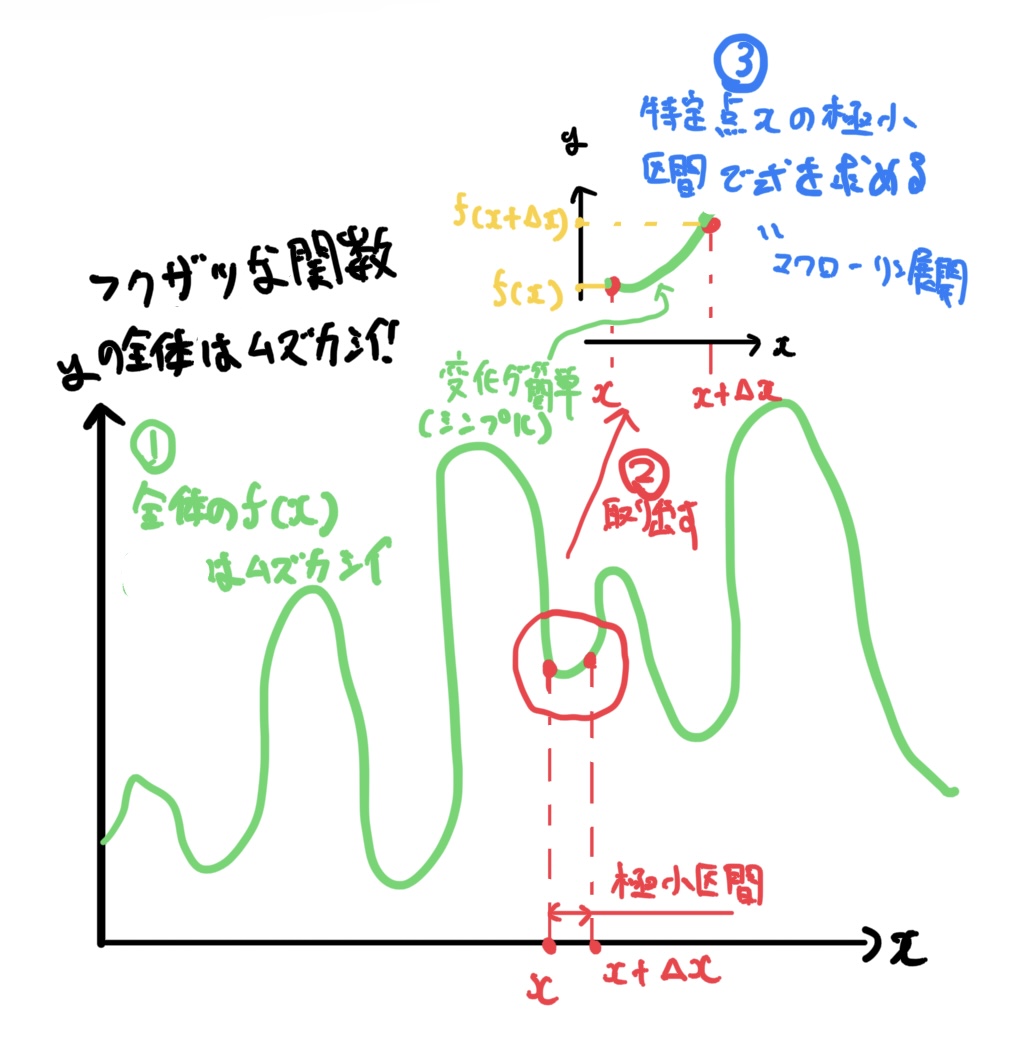
全体の関数は難しくても特定の極小範囲だけを取り出すと意外とシンプルな関数になり解明しやすくなります。
このように特定の極小範囲に着目して複雑な関数をシンプルな関数に変換(本当は展開)することをテイラー展開と呼びます。
当然ながら極小範囲に着目しているので複雑な関数全体に適用することはできませんが局所的に使用することには十分です。
このテーラー展開の中でも原点まわり(x,y)=(0,0)でシンプルな関数に展開することをマクローリン展開と呼びます。
一応、マクローリン展開(微分を使う)の定義式を載せます(混乱したらごめんなさい)。

こんな感じで人類は全体では複雑なモノでも局所的、部位ごとに分解してシンプルにして考えることによって進化しています。その一手法がマクローリン展開になります(他にもフーリエ変換とかいろいろある)。
こんな感じで工学でも数学が非常に重要なのでもし学生、若手エンジニアが見てたら頑張って下さい。またノギスのような身近な道具(身の回りの全ての道具)でも数学が非常に大きな役割を果たしているので学生時代に数学苦手だった方も興味を持って頂けると人生を得すると思います(その内にもう一度学ぶ、数学講座みたいなのをやって見ます)。
さて測定誤差に戻ります。
マイクロメーターの計測誤差(アッべの原理)
まずはマイクロメーターの外観です。ちなみに英語もマイクロメーターで一緒です。

ノギス同様にマイクロメーターの各部名称、使い方はここでは省きます(要望があれば書きます、工学系の学生は初等実験のテストで必ず出題されます)。
次にマイクロメーターである物体を測定した状態を描いてみます。
理想的(完璧)なマイクロメーターであれば理想の測定結果Aが得られます(ノギスと同じ)。
ここで重要なのがマイクロメーターは測定軸とスケール軸が同軸です(アッべの原理を満たす)。ここがノギスとの計測の論理構造の決定的な違いになります。
しかしながら実際にはガタが発生するので理想通りには計測できません(ノギスと同じ)。
次に複数存在するガタ、ズレの中で測定誤差が最も大きくなるガタを考えます。
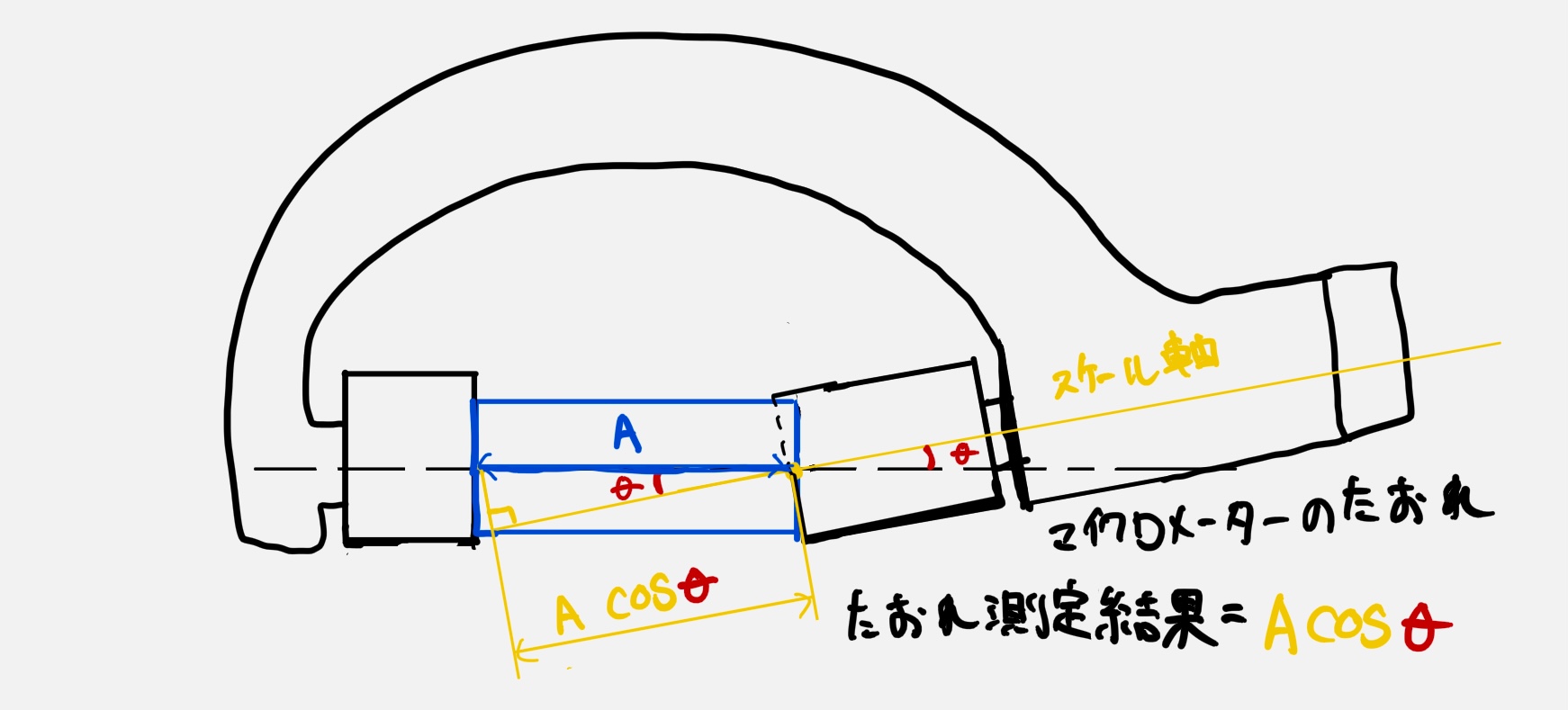
測定に最も影響を与えるのはスケール軸の倒れ(倒れ角をθと定義)になります(ノギスと違う点が重要)。
ここで倒れ角θを利用して測定結果を式にすると次のようになります(単純な三角関数、図形問題)。
$$ 倒れ測定結果=A\times cosθ $$
次に発生した誤差を求めるのは単純に理想的な測定結果から倒れ測定結果を引けば求められます(測定誤差をε:イプシロンとする)。
$$ 測定誤差ε=理想測定結果ー倒れ測定結果=A-A\times cos θ=A(1-cos θ) $$
になります(ノギスと同じ)。
式だけだと誤差のイメージが湧かないと思うので横軸をθ、縦軸を測定誤差εのグラフにします。
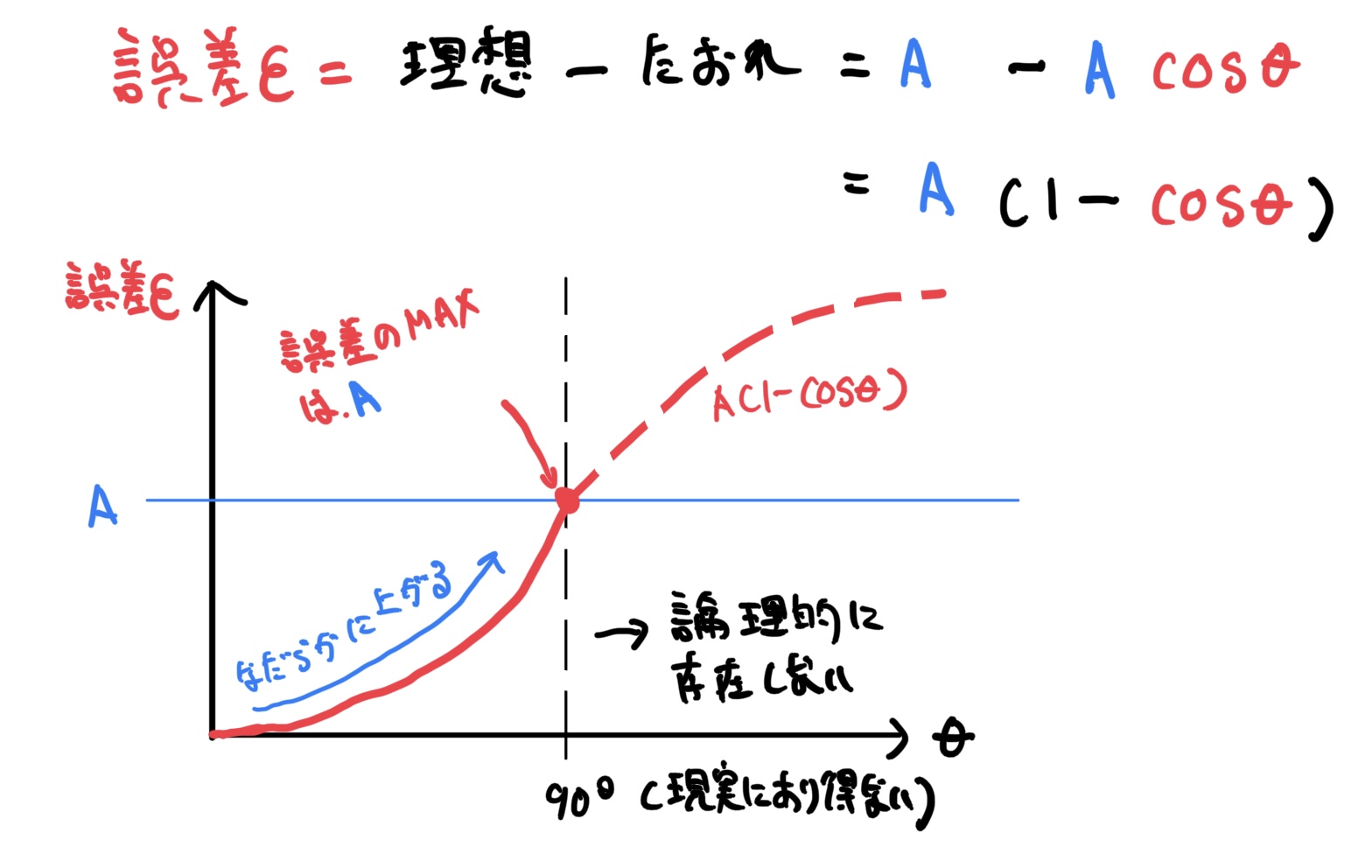
グラフの通り誤差はA(1-cosθ)なので倒れ角θが増加すればなだらかに増加する、極端に考えると倒れ角が90°(現実にも論理構造にも無い)の誤差はAになります(ノギスと違って無限にならない、収束する)。
ノギスと同じように多くの方が“実際の倒れ角θはかなり小さいので誤差も大したことがないだろう“と考えると思います。
なので次にθがかなり小さい(極小)時の誤差の大きさを詳細に考えてみます(θが0°付近)。
式がcosのままでは角度θが極小の時の変化が分かりにくいのでcosをマクローリン展開します。

ここで展開した全ての項を使うとややこしくなるので3次成分$(θ^3)$までを使います(工学では基本的に2〜3次までで十分とする)。
また実際には展開した式ではθは角度(°)ではなくラジアン(radian、弧度法、角度180°=Π)にして計算します。
cosを展開式の3次の項までと交換して誤差εを求めます。
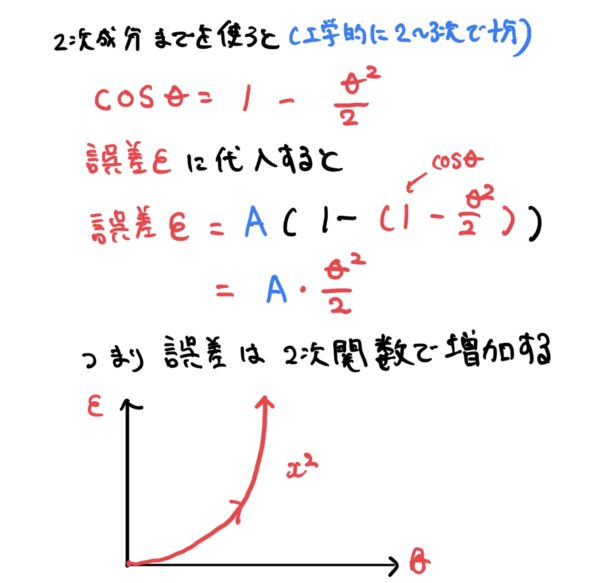
つまりマイクロメーターにおける計測誤差εは倒れ角θの2次に比例して大きくなるのでそこそこ大きさであることがイメージできると思います。
なのでノギスの3次に比較しマイクロメーターは2次に比例する誤差なので圧倒的に誤差が小さくなります。
このようにスケール(尺度)が測定軸と同一軸にあると誤差が小さい原理をアッべの原理と呼びます。
これがマイクロメーターの計測方法が持つ論理的な誤差の大きさになります(これもマジで試験に出題される)。
ノギスとマイクロメーターの計測誤差の比較
ここまででノギスとマイクロメーターの誤差を計算したので比較します。
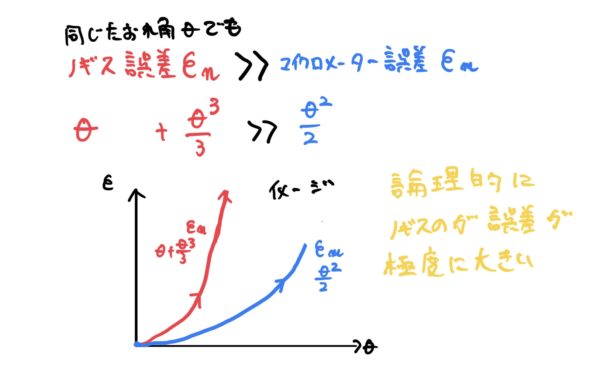
絵でわかると思うのですが同じ倒れ角θでも圧倒的にマイクロメーターのが誤差が小さくなります。
あり得ないですがノギス、マイクロメーターの倒れ角を1°(およそ0.017[rad])として計算すると
ノギスの誤差がおおよそ0.017
マイクロメーターの誤差がおよそ0.000145
になりおおよそで全く同じ倒れ角1°でおよそ100倍も精度が変化します(機器の製造精度とは全く関係なく手法に依存する)。
この論理的な特性によってノギスをどれだけ精密に製造しても絶対にマイクロメーターには敵わないことが理解できると思います(マイクロメーターの精度0.005mmに対してノギスが余裕で10倍の0.05mmの差に繋がる)。
またノギス、マイクロメーターだけに関わらず全ての計測機器において尺度が同軸か否か、つまりアッべの原理に従うかどうかで精度が決定的に決まります(全く同じ機器でも手法だけで平気で精度が100倍程度は変化する)。
よって計測機器(物理測定、電子測定など全て)を観る時に尺度(スケール)がどこについているのかに注目すると面白いと思います(スケールをどこで取るか!)。
話を広げるとこの理論も含めて計測工学≒センサー工学なので計測に限らずあらゆる製品の制御に必要な光学センサー(電装ガンのFCUセンサ)、磁気センサーまたはホール素子センサー(電動ガンのFCUの磁気センサー)、電位センサーまたはポテンショメーターの解像度、正確さに関わる重要な基本になります(気が向いたらセンサーも解説します)。
なので工学系の学生やエンジニア(機械、電気は当然ながら流行りの組み込みソフトウェアのSEも)にとって重要なことだと思います。
まとめ

自分の手持ちのデジタルノギスの電池交換から話題が飛躍し計測工学の初歩までを説明しました。
アッべの原理に基づきノギスの限界精度が0.05mm、マイクロメーターの限界精度が0.005mmとイメージすると間違いはないと思います(原理の違いで10倍の差)。
つまりエアガンの弾のよくある直径5.95±0.01mmは公称5.95はノギスでギリギリ測定できるが公差0.01はマイクロメーターを使わないと測定できないことになります(マイクロじゃないと意味がない)。
また弾に限らずデジタルノギスの0.01mm寸法は取り敢えず見せてるだけ(極端に考えるとデタラメに近い)で0.05mmで考えないと正確でないです。
ただし精度が悪いからノギスが全くダメというわけではなくノギスが持つ良い特性である測定が簡単、比較的大きなモノが測れる、コストが安い(価格が安い)ので適材適所です。
以上、長くてマニアックな内容になりましたがお付き合いありがとうございました(工学系の学生はこの内容は必ず試験に出題される、エンジニアは必須だと思います)。
・高精度デジタルノギス(ミツトヨ)
記事頭で紹介したノギスと異なり高精度ノギスです。プロスペックのミツトヨです。普通に使う分には必要ないレベルで記事頭ので十分だと思います。
・アナログノギス(ポケットノギス)
デジタルにはない信頼性、コンパクトさ(デジタルはでかい)で一本あると便利です。私も仕事中は必ずポケットに入れてました。
・マイクロメーター
日常で使う機会は少ないと思いますが弾を計測する、ミクロン(0.005mm)の世界に入る場合には必要になります。紹介はアナログですがデジタルもあります。
個人的なお勧めで私はエアソフト本体やパーツ関連の多くをアマゾンのプライム会員に入って購入しています。
意外と本体、パーツ共にラインナップが充実していて最安値では無いもののそこそこの低価格で安定的に購入できるので重宝しています(小物だと買いに行くのがめんどくさいので重宝)。
多くの商品が配送料無料、お急ぎ便無料になり速ければ次の日に到着します。さらに会員になると映画、アニメ、音楽、書籍なども多くの作品がフリーで見れます。
月間プランだと月600円からで年間プランだと年で5900円でかなりのお得で会員は対象商品購入(エアソフト関連も大抵、対象になっている)でポイントが還元されます。
まずは無料体験からお勧めします。








コメント