今までは公差の持つ意味と複数部品の公差の足し合わせの理論を説明してきたが、実際にどうやって複数部品を組み合わせた場合の公差計算(緊度計算)を説明していく。
まず言葉の定義だが、複数の公差を持った寸法を足していく計算を緊度計算と呼び、集積した公差を累積公差と呼ぶ。
単純に複数の部品の寸法を足すだけなら簡単だが、足したり引いたりする必要がある場合は混乱することがよくある。
なので今回は公差を持った複数の寸法の取り扱いについて説明していく。
さらに累積公差に関しても寸法同様に単純に足すだけで済まない場合(二乗平均公差とか)があるので緊度計算と累積公差が求められる表計算例(EXCELなど)を紹介する。
公差の意味の詳細は、初心者でもわかる寸法公差って何だ?(工程能力指数 Cp Cpk)

公差の足し合わせの理論の詳細は、初心者でもわかる複数部品の公差の積み重ね(累積公差、二乗平均公差、絶対緊度)
今回の記事を書くに当たって少しネットで調べたが2次元での公差計の有料ソフトが存在していることに非常に驚いた。
今回の説明を読んでいただければそんな有料ソフトなんか必要がないことがわかってもらえると思う。
例題の設定
では、まず例題の設定をしていく。
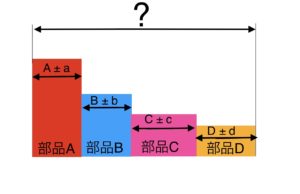
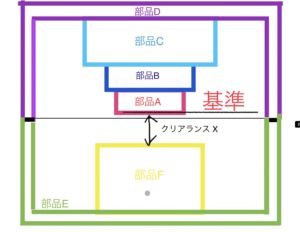
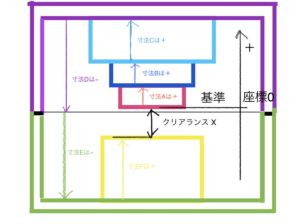
次の図のような6部品を設定する。
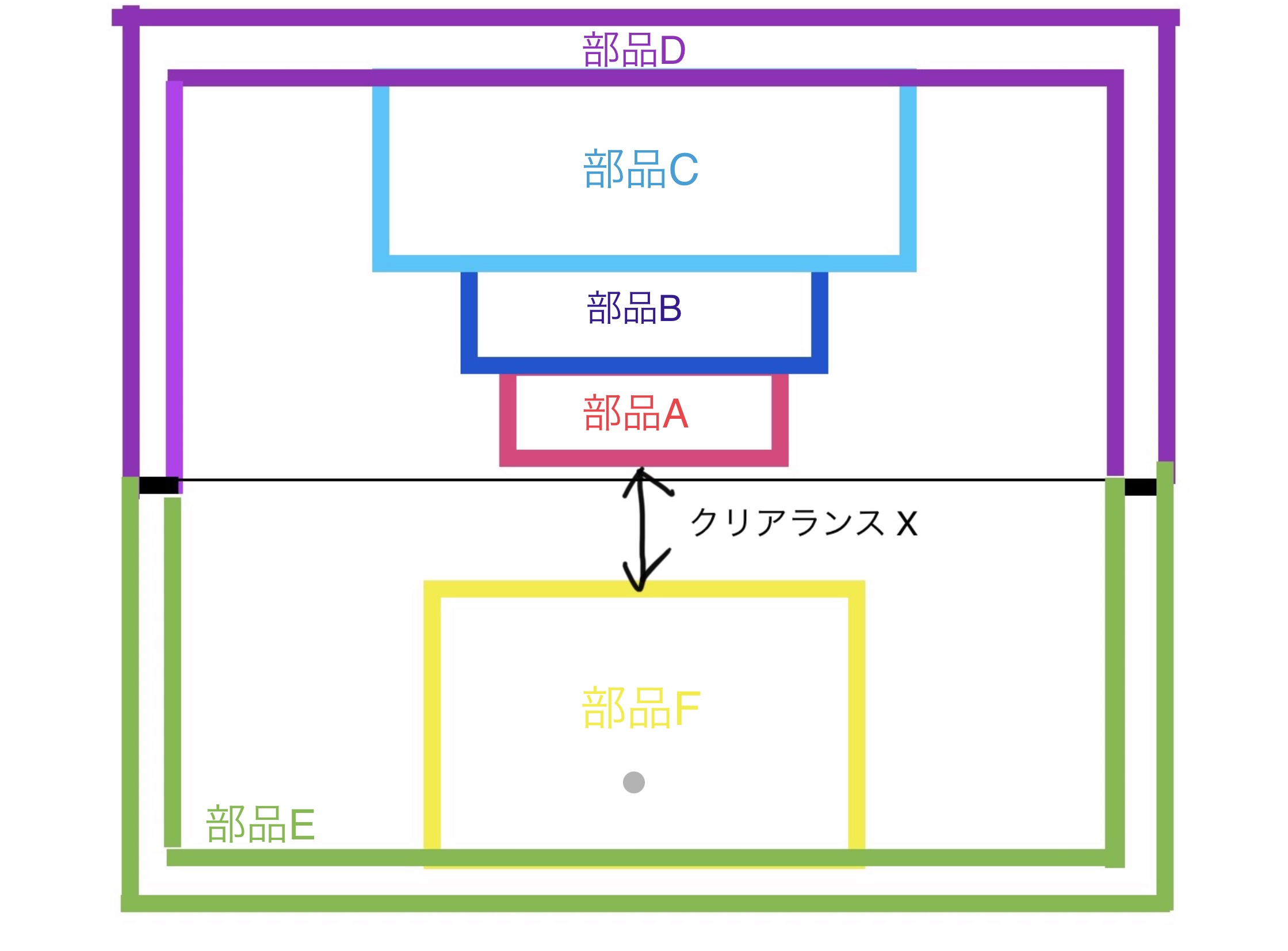
部品のイメージとしては部品A、B、C、Fが円盤の断面で部品D、Fが円盤を中に収める箱のようなものの断面だと考えて欲しい。
これらの6部品から発生するクリアランスXを求めていく。
例題のクリアランス計算
まず、始めに行うことは図の中で基準を決めることが大切。いきなり寸法は拾わない。
この基準の設定で緊度計算の7割くらいの重要度がある。
ここでいう基準は単品図で言えば寸法をどこから引くか決めることと同じである。
1,基準を決める
まず最初に基準を決める(スタート基準)
クリアランスXを求めたいので基準は図のようにとる。
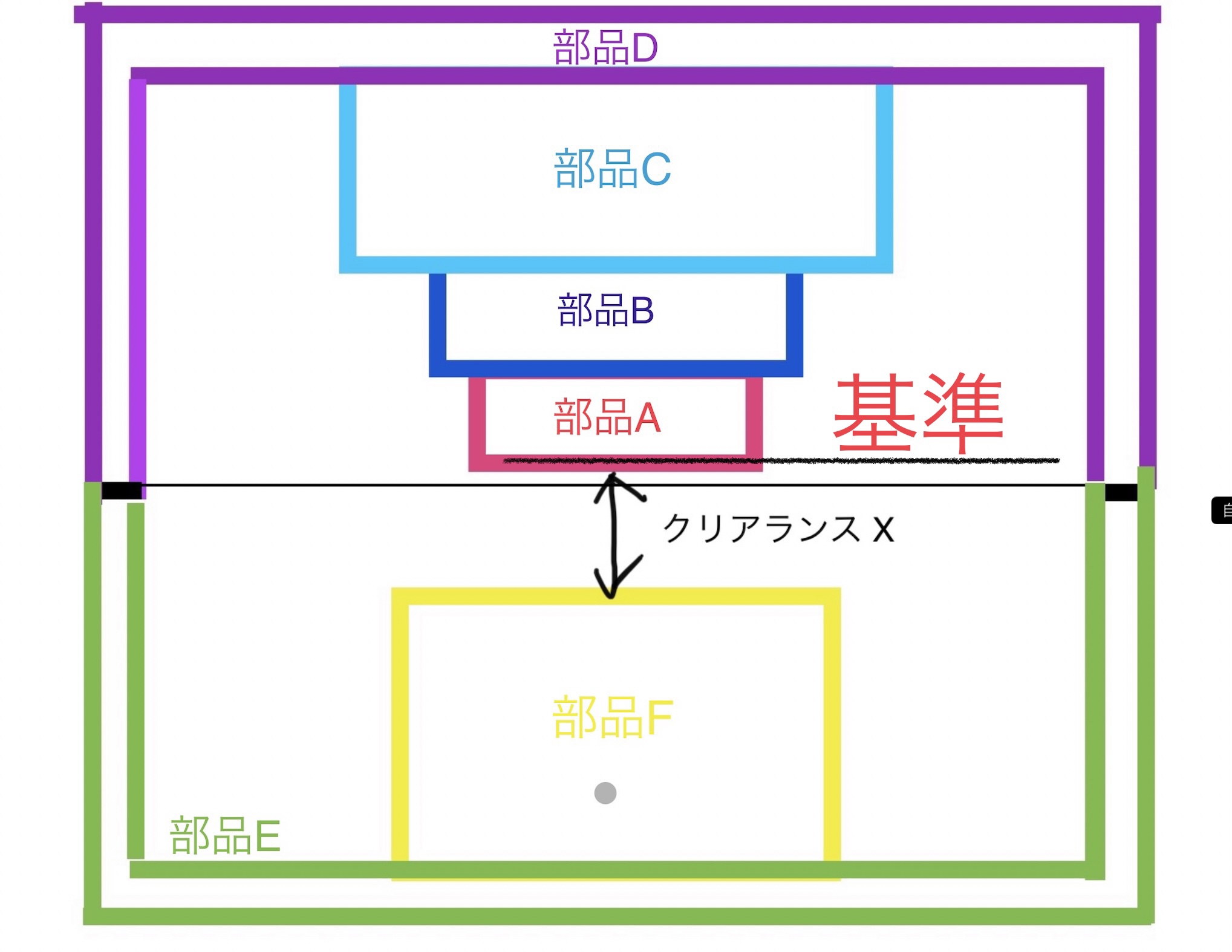
クリアランスXを求めたいのでクリアランスXの位置と部品Aの端面を基準とする(部品Fの端面を基準にしても良い)。
2,方向を決める
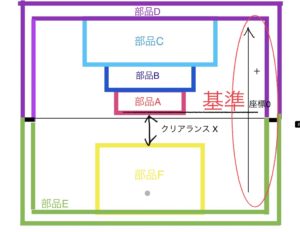
基準からどちらの方向を+の寸法と見なすか方向を決める。基準を原点とした座標軸を設定し方向を決める。
早速、決めて行こう。
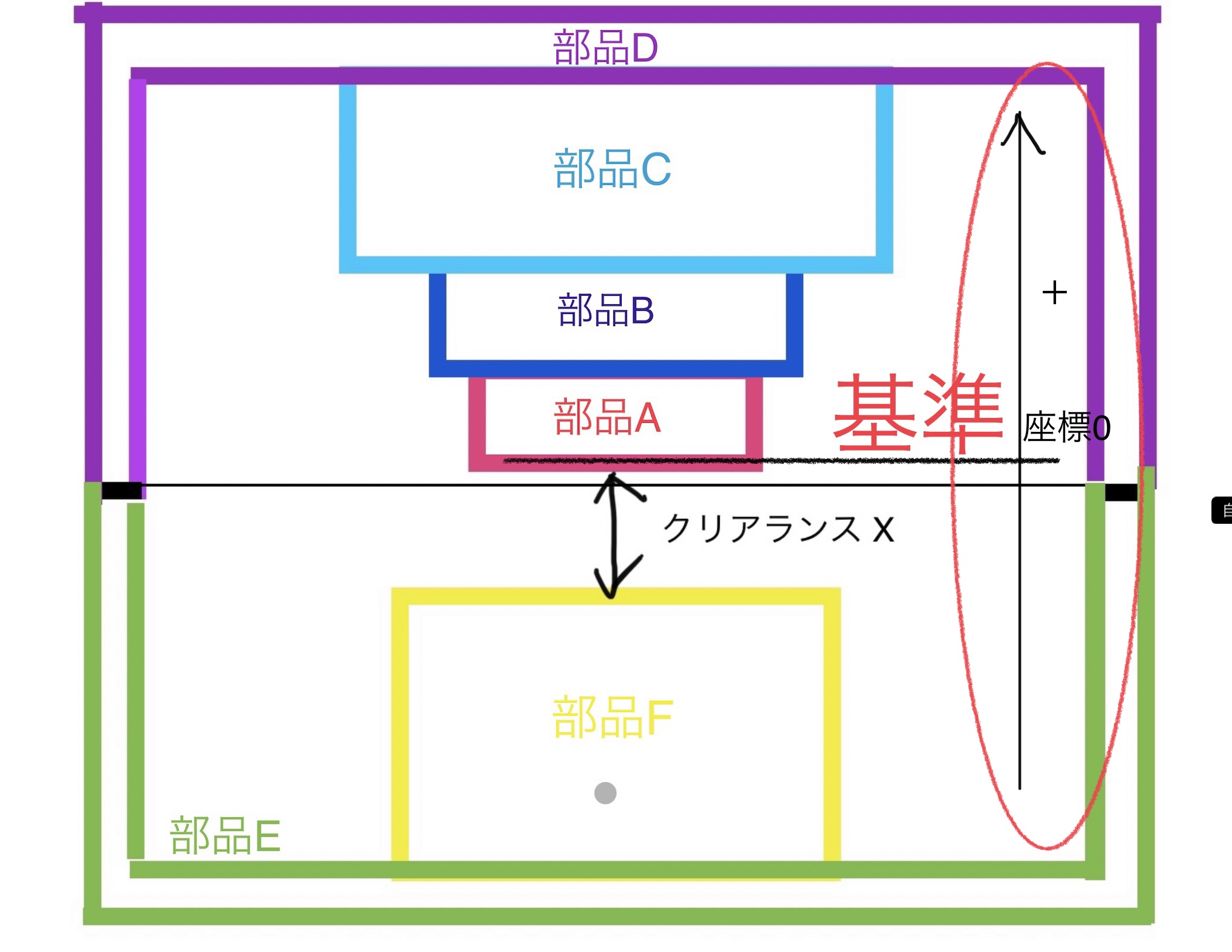
図のように基準を座標原点の0として図で上に行く方向をプラスとし逆はマイナスとした(逆でも大丈夫)。
3,寸法の表記を変える
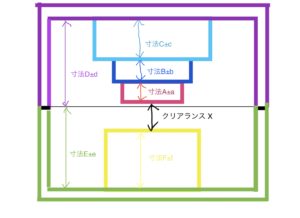
関係する各寸法を確認していく。各寸法の形を中央値±公差の形に変換する。
ここでやることは関係する寸法を抜き出して、寸法の形を中央値±公差の形にして変換する。
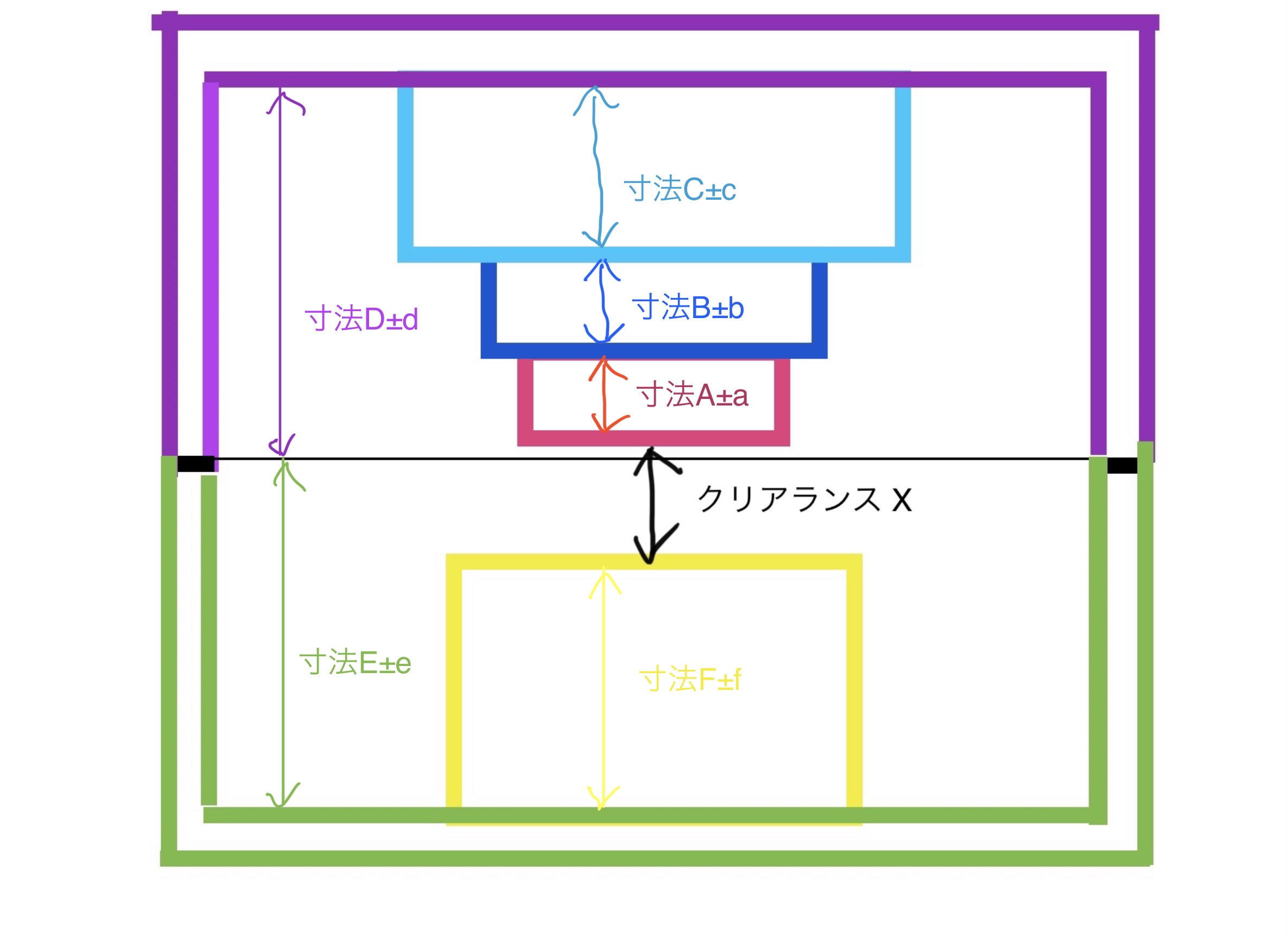
ここまで来れば図でやることはもう少しだ。
4,符号を決める
2で決めた座標軸に基づいて各寸法の符号を決めて、振っていく。
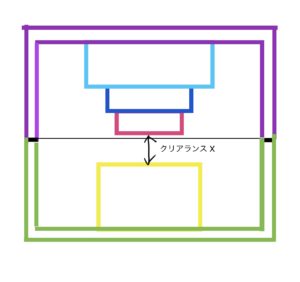
文章では伝わりにくいので実際に図で実施する。
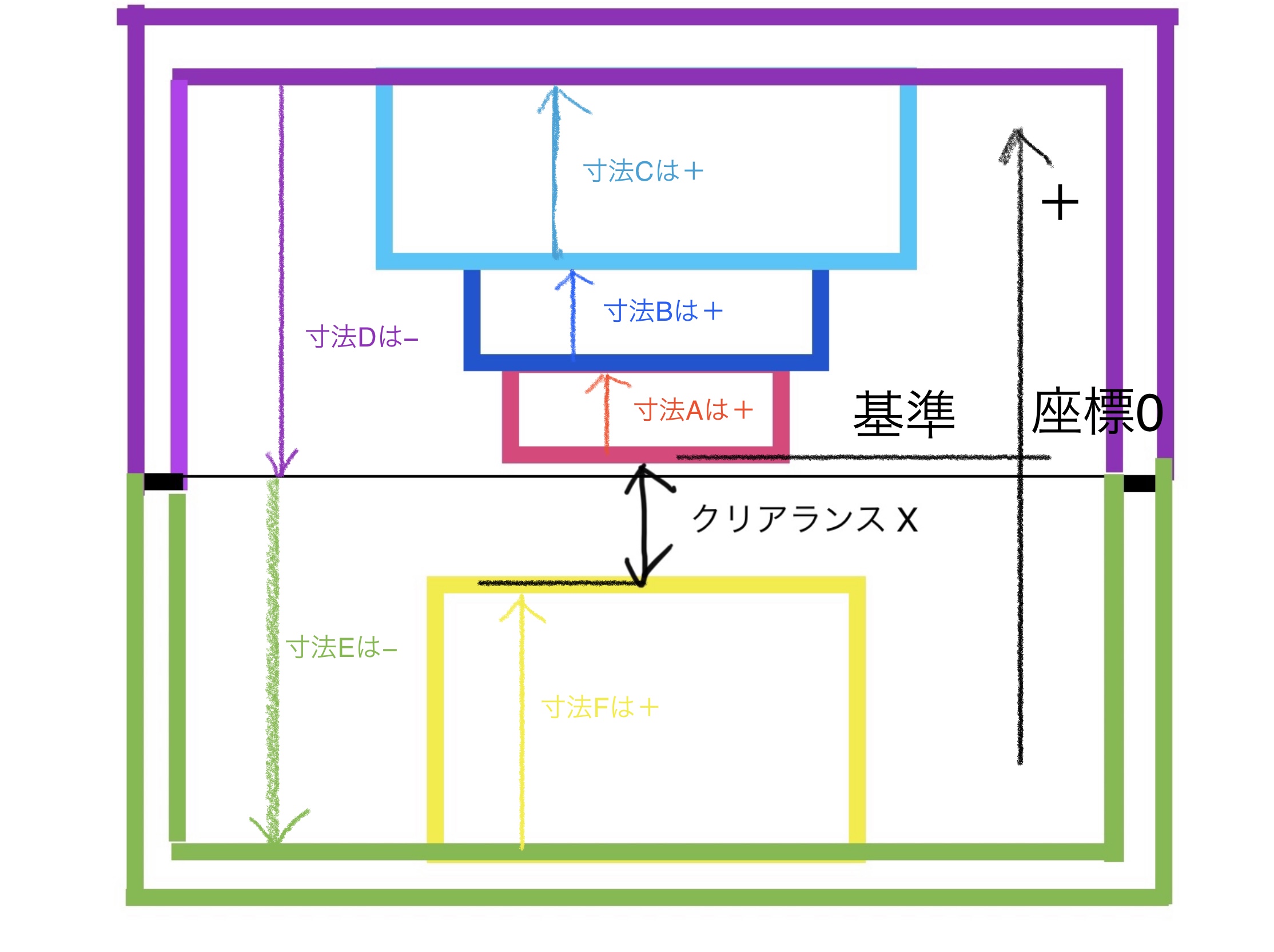
これでもうわかったんじゃないかな?クリアランスXまで図で辿れるようになる。後はただの数値計算になる。
おさらいしよう。
ここまで図上でやること。
実際にやるときはレイアウト図と各部品図を紙に印刷してマーカーなどを使って手でやることを強く勧める。
多くの人が頭の中でミスなく実施するのは難しい。
では数値計算を説明しよう
クリアランスXを数値で求める
ここからは表計算ソフト(EXCELとか)を使っていくことを勧める。
まず、これまでに解っているデータを次の表にする。
解っているデータは、部品名、基準、座標、方向、寸法、符合である。
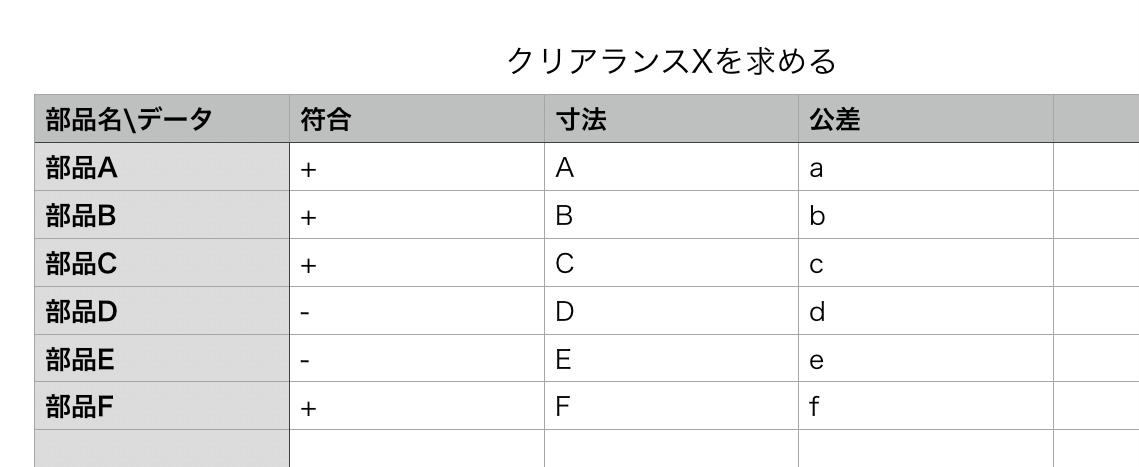
こんな感じで表をつくる。
コツは下の図で説明する。
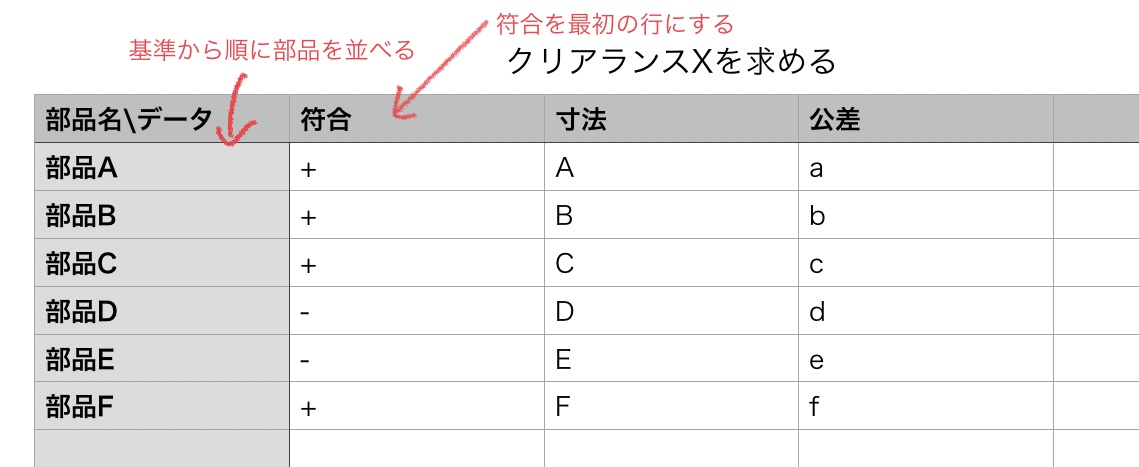
後はただの掛け算と足し算で決まる。
クリアランスX= (符合×寸法の和) ± ( 公差の和 )
だから計算すると
クリアランス X=(+A+B+C-D-E+F) ± (a+b+c+d+e+f)
で計算できる。
ただこれだと単純な累積公差しか求められないため二乗平均公差が求められるように表を追加する。
また後で確認しやすいように表を少し改造する。
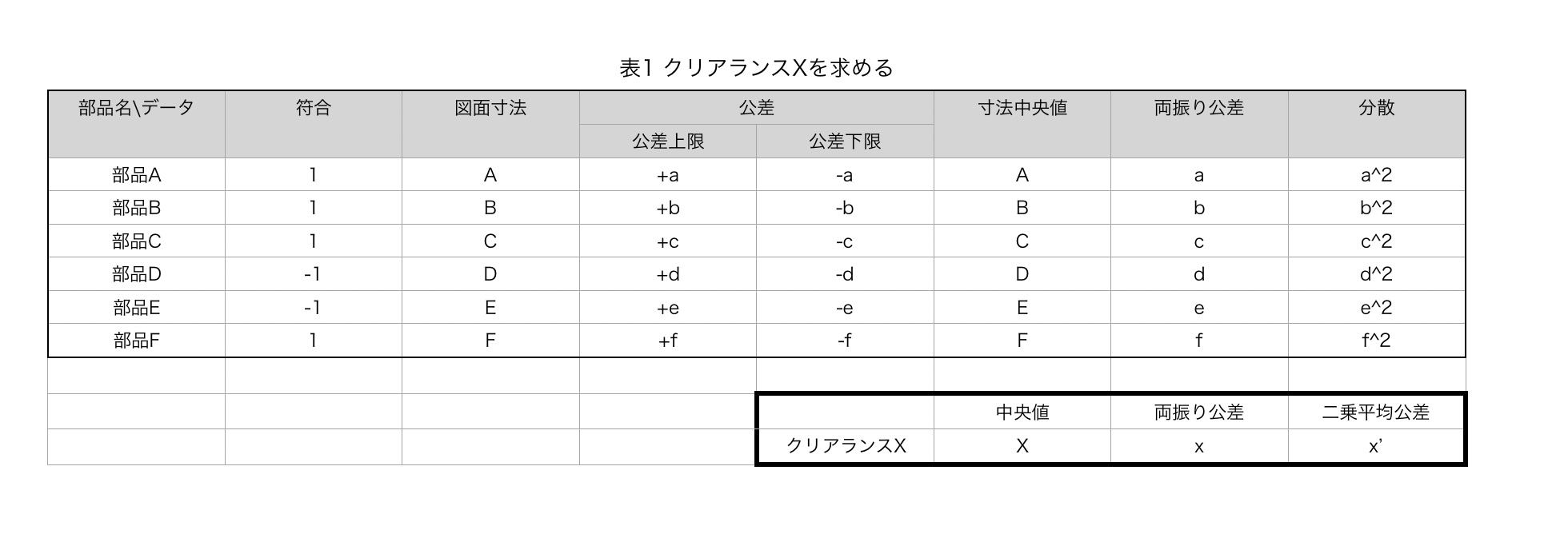
こうするとクリアランスXの中央値、公差、二乗平均公差がわかる。いきなり表がパワーアップしているので説明していく。
累積公差の計算表の内容詳細
表の左から順に見ていく。
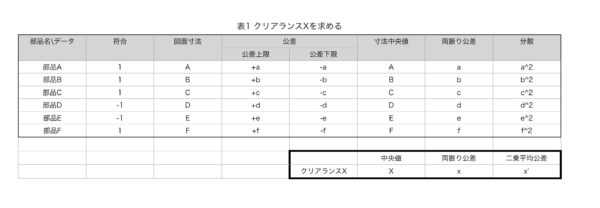
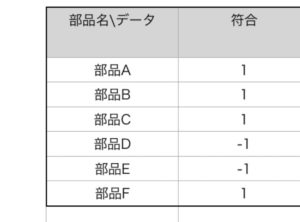
符号については表計算で計算しやすいように+を1、ーを−1としている。この手法を取ると実際に入力するときに速くなるのでオススメ。
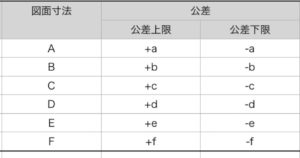
図面寸法、公差上限、公差下限は図面の値を入れられるようにしておく。ここでは中央値±公差の形ではなく図面値をそのまま入れるようにしておく。
寸法中央値は表計算のセルに$ \frac{(図面寸法+公差上限)+(図面寸法+公差下限)}{2}$と入力すれば算出される。
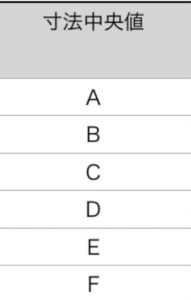
両振り公差については公差を$ \frac{公差上限-公差下限}{2}$と入力すれば算出される。
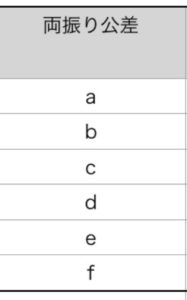
分散は両振り公差を2乗する。
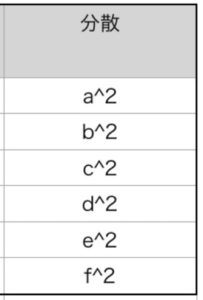
クリアランスXの中央値は$ 符号X寸法中央値 $を足し合わせる、両振り公差は部品の両振り公差を足し合わせる、2乗平均公差は分散を足し合わせて最後に平方根を取れば算出される。

このような表を表計算ソフトで作成しておけばクリアランスXの上下限や二乗平均公差がよくわかる。EXCELなどで簡単に作成できるので是非、試してほしい。
また各図面との照合もやりやすいので見返すときに有用であると思う。
例題2 歯車の噛み合い幅を求める
では、次のような図で歯車の噛み合い幅を考える。
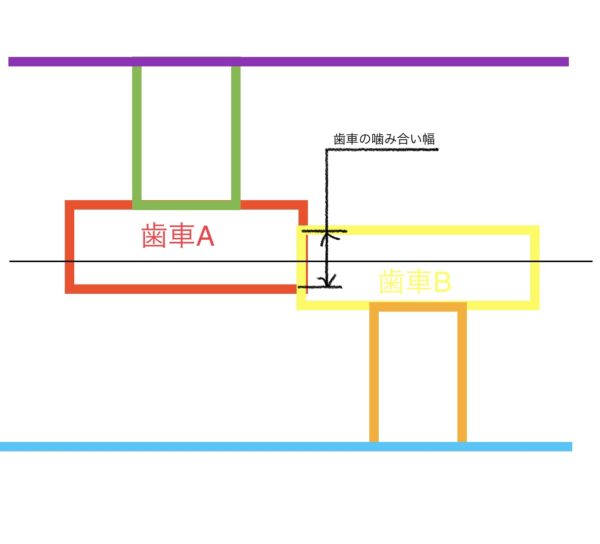
説明した通りまずステップ1で基準を決める。この場合は二パターン考えられるが、どちらでも良い(歯車A基準と歯車B基準)。
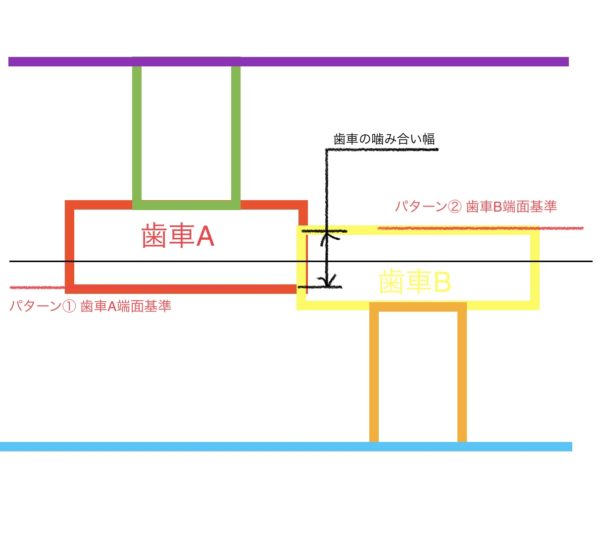
ステップ2に移行して座標と方向を決める。
図のパターン①を採用して座標原点と向きを決める。
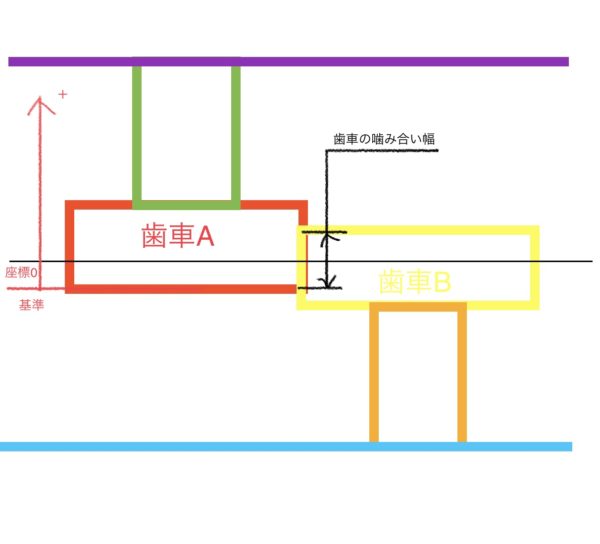
ステップ3に移行して計算に必要な各寸法の抽出と寸法の形を整えて中央値±公差にする。
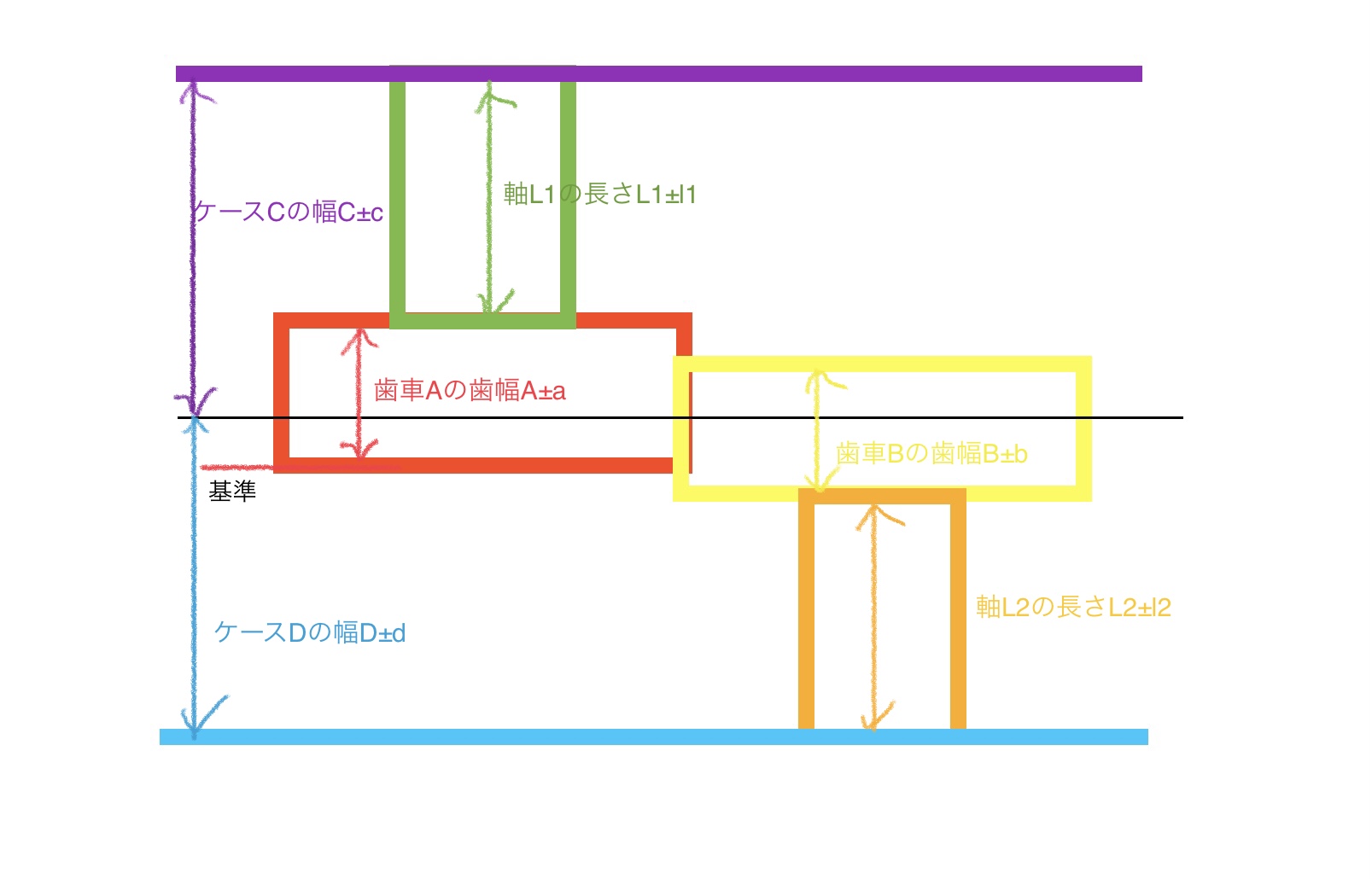
ステップ4び移行してステップ3で決めた座標軸に従って各寸法の符合を決める。
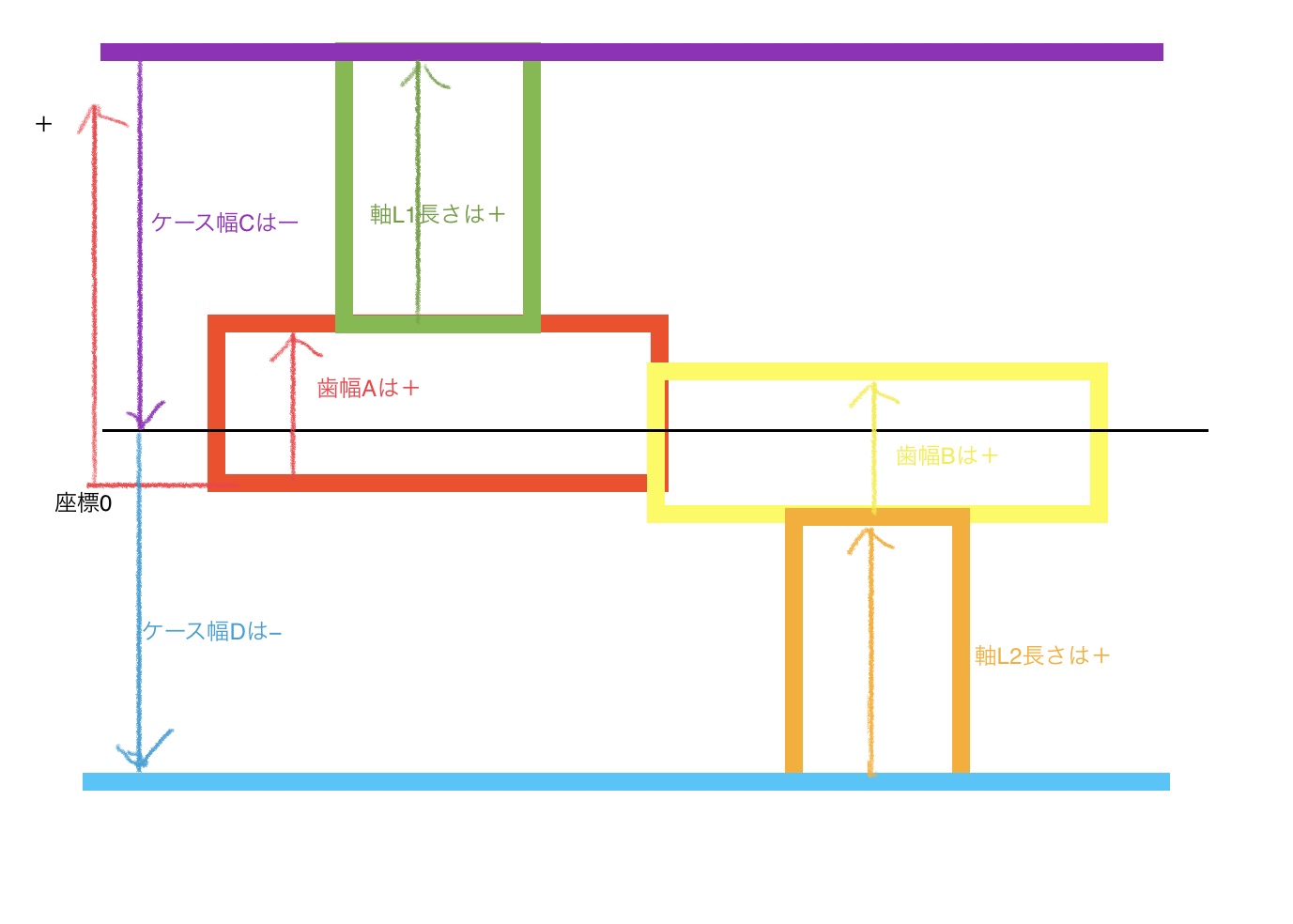
最後に表に値を入れて計算すれば累積公差がわかる。
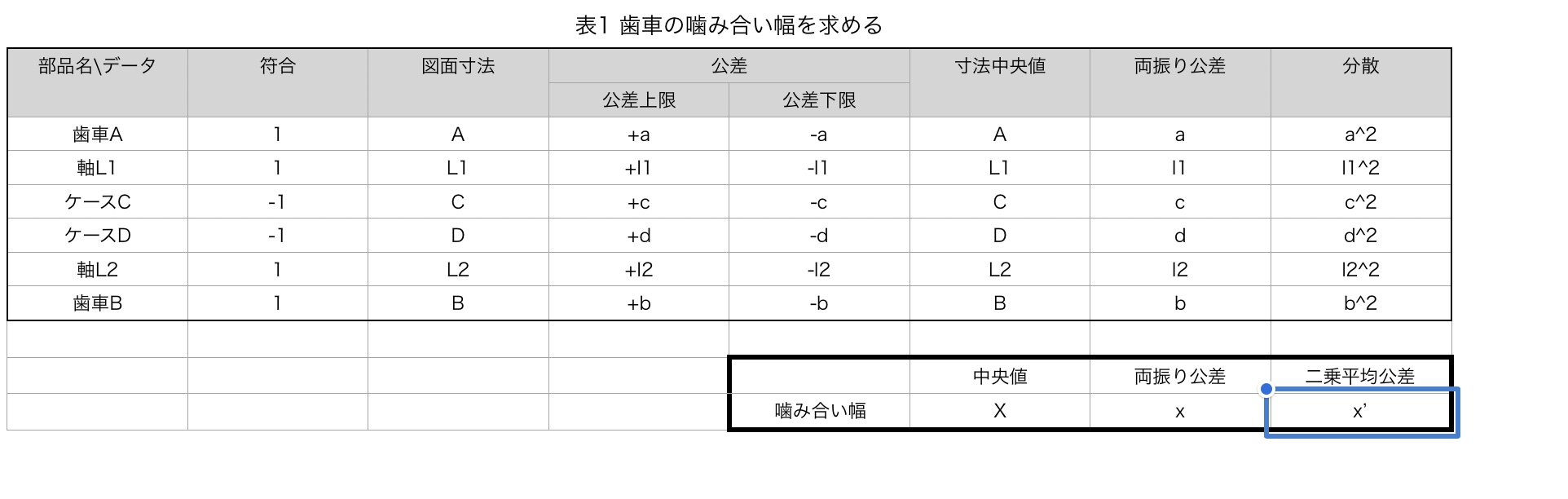
どうかな、できたかな?
まとめ
ここまで説明してきた方法でどんなに複雑な製品でも地道にやれば公差計算が必ずできる。
まあ幾何公差や軸受のガタなど少し取り扱いに知識が必要なものがあるが考え方は一緒である。
繰り返しになるが、まず、大前提として必ずレイアウトと各部品の単品図を紙で容易する。
後は紹介した表を作成すれば求まる。

ここで大切なことは、図面の読み方で紹介したように3Dだけではこのような公差を含めた計算を実施することが難しい。
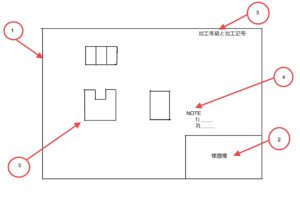
だからこそ今の時代でも2D図が読める、書ける技量は絶対に必要なのだ。(3Dモデルが公差中央でできていて公差データが入り公差解析ツールがある場合のみ3Dだけで求められる)
また2D図が有れば特殊なソフトやデバイスは、全く必要なく表が有れば必ず求められる。
慣れないと大変だが練習すれば必ず誰でもできるようになるので是非、真似してみて欲しい。
次回の公差編は、幾何公差の意味と使い方をやりたい。
ここでオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
今回の記事で紹介した内容に関連する品質(QC)の考え方、統計学に関連する本が安く読める。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
折角なのでさらに機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。





コメント