これまで3回に渡って梁の説明をしてきた。今回はその集大成で梁のたわみを求めていこうと思う。
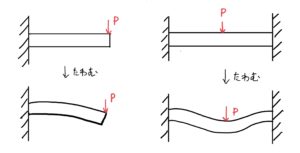
この梁のたわみを求めることはとても重要で、これが求められないと機械構造物の変形量が計算できない。
確かに今まで丸棒のねじりや引張り、圧縮による変形を説明してきたが、それだけでは機械構造物の変形量は求められない。なぜならばそれらは物体内の曲げモーメントによる変形が考慮されていないためだ。
機械構造物はさまざまな形状が複雑に絡み合って構成されていて、一つ一つ分解するといくつかの種類の単純な梁の組み合わせに分解できる。
よって今回、説明する梁のたわみがわかればそれぞれの変形量がわかり足し合わせれば機械構造物全体の変形量がわかる。
これはコンピューターシミレーション(CAE)でも同じような処理をして計算することが多い。
ここまでで重要さがわかってもらえたと思う。これから説明するが是非、理解して欲しい。
また多少、数学のテクニックを使うが難しくないので言葉に惑わされないようにしよう。
たわみ曲線
まずはたわみを求める前にルール、決まり事、基準を決めないと何事も始まらない。
まず基本的な決まり事を説明する。
いつも通り例題を設置する。
単純な両持ち梁で真ん中に荷重Pを与えられ変形した梁を考える。座標は横にx、変形する方向(下)をyとする。

ここで変形したはりの中立軸(中央の線)をたわみ曲線又は弾性曲線と呼ぶ。
さらに任意の場所での下方向の変位yをたわみ、その場所のたわみ曲線の接線と元のはりの中立軸との交わる角度をたわみ角と呼ぶ。
ここで注意なのだがいつもながらしつこく言うがたわみの符合は図で下方向(変形する方向)を+とし、たわみ角は時計回りを+とする。
これがとても重要だ。
決まり事はこれだけなので是非、頭に入れて欲しい。
次に梁のたわみとたわみ角を求めていく。
たわみ曲線を求める
まずは先程の例題を思い出してもらって
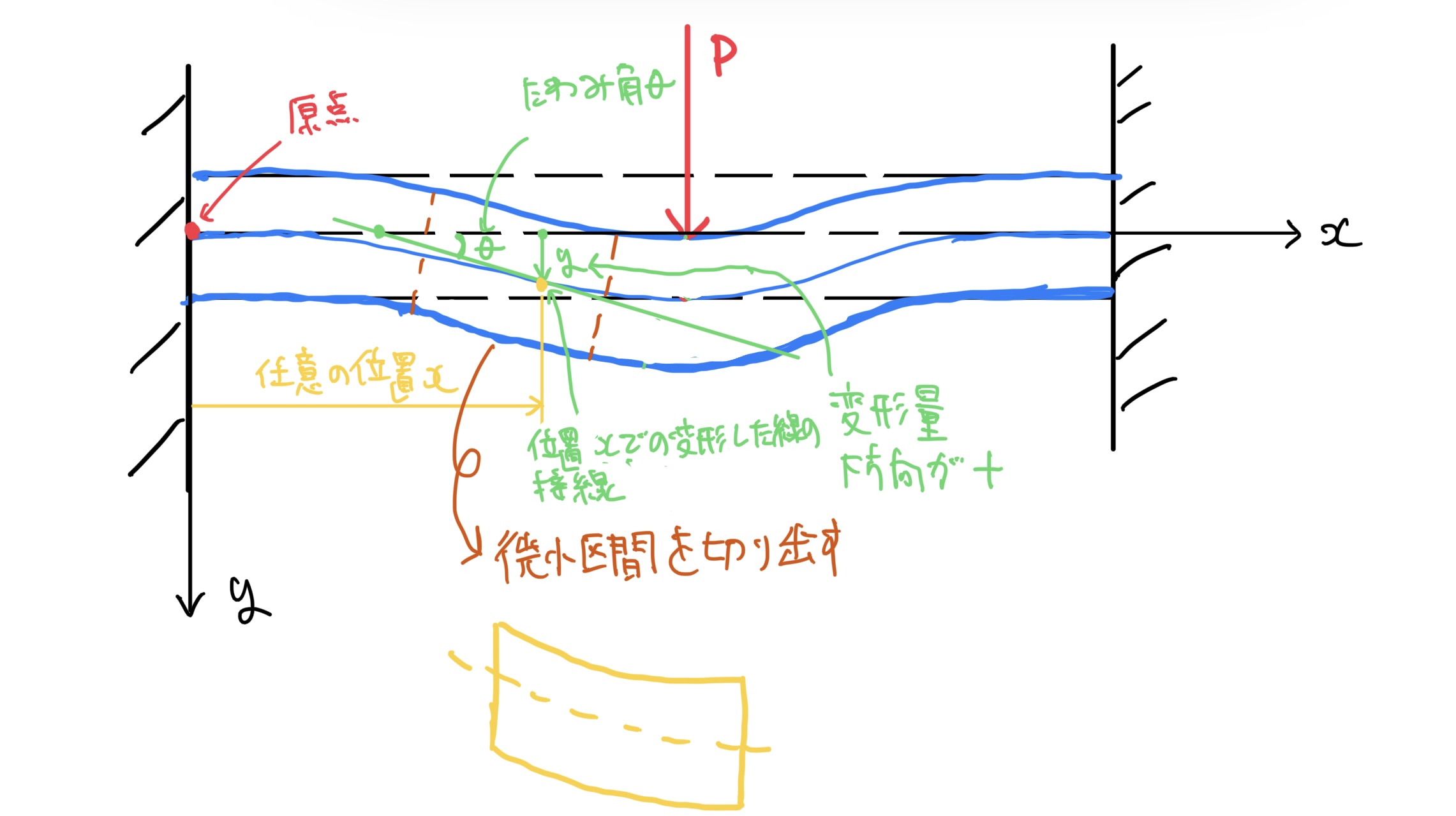
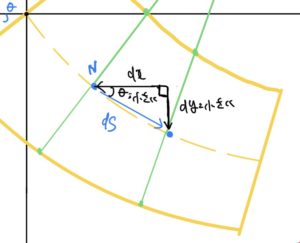
一気にたわみは、求められないので毎度の手段である微小区間を切り出して考える。今回は図の黄色の破線の部分を切り出してみよう。
切り出した図はこちら。すでに様々な記号が振られているが一つ一つ見ていこう。座標を含めた設定は同じまま。
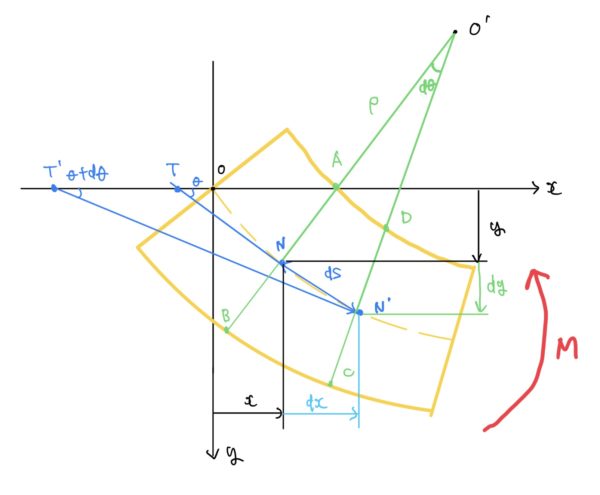
まずはρ(ろう)という記号だがこれは曲率半径を表している。簡単に言えば変形の形を円弧と考え、その円弧の半径をρで表している。
次に曲げモーメントMに関してだがこれは前々回で説明した通り。
これまでの説明でははりの内部には曲げモーメントMと共に剪断応力も発生しているのだが、たわみ曲線では曲げモーメントによる変形が支配的で剪断力によるものは小さいので無視をする。
後に剪断力による変形が何故、小さく無視できるのか?無視できない場合もあるので説明する。まずはないものとして考えてくれ。
次に点N-N‘間の長さdsについて考えていく。ここで長さdsは円弧になり求め方は半径×角度で求まる。つまり曲率半径ρと角度N-O’-N’ (-dθ)の掛け算で求まる。
ここで“何故、角度が−の符合を持つか”というと長さdsが増加すると角度は増える。長さdsが増加すると点の動きを見ると点N’がNからどんどん離れていく。そうすると角度は、反時計回りに増加する。そう、ここで決まり事の時計回りが+と決めているので角度dθはーなのだ。
ちょっとややこしいので図を見ながら脳内で点N‘と点T‘が元の点Nと点Tから離れて行くのをイメージして欲しい。そうすれば角度N‘ーO‘ーNが反時計回りに角度が増加して行くことがわかると思う。
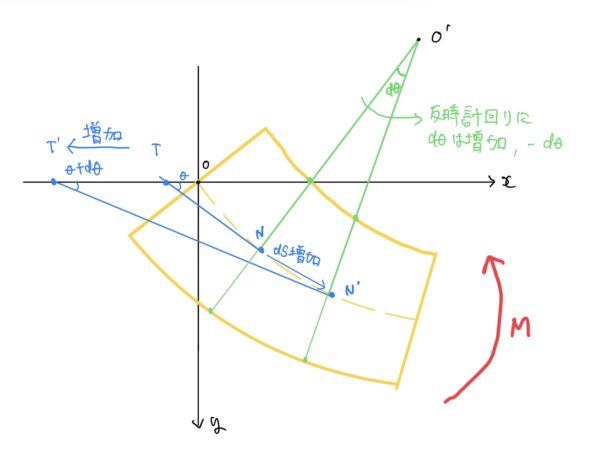
図を元に戻してここから式を立てて行く。

まずは長さNN’(ds)と点O’の角度dθの関係の式を立てる。
$ ds=ρ(-dθ)、\frac{1}{ρ}=-\frac{dθ}{ds} $
一方でたわみ曲線の傾き(中立軸の傾き)は、(円弧N-N’の接線と変形前の中立軸の交わる角度)
$ \frac{dy}{dx}=tan(θ) $
ここで角度θがかなり小さいので次の式が成り立つ。
$ ds=dx(角度が浅いのでdyを無視)、θ≒tan(θ)=\frac{dy}{dx} $
とすると曲率半ρとdx、dyの関係式は、次のようになる。
$ \frac{1}{ρ}=-\frac{dθ}{ds} =-\frac{d}{dx}(\frac{dy}{dx}) $
$ \frac{1}{ρ} =-\frac{d^2y}{dx^2} $
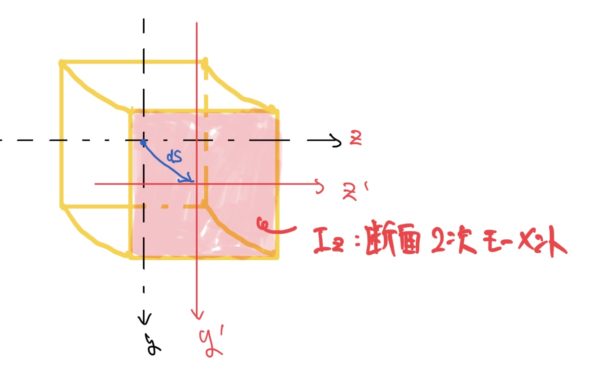
ここで”断面二次モーメントって何だ”を思い出して欲しいのだが曲げモーメントMと曲率半径ρには次の関係式がある。
Izは断面二次モーメント、Eは材質の弾性係数。
$ \frac{E}{ρ}Iz=M、\frac{1}{ρ}=\frac{M}{EIz} $
よってたわみの式は次のようになる。
$ \frac{d^2y}{dx^2}=-\frac{M}{EI} $
yとxは最初の定義通りyがたわみ量、xが座標なのでy=f(x)はたわみ量の関係式を表すので$ \frac{d^2y}{dx^2}はy=f(x)を2回微分した式、つまりたわみの微分方程式になる(Iはz軸の断面二次モーメント)。
ここで重要なことは断面二次モーメントが分母にいる、つまり断面二次モーメントが大きければたわみ、たわみ角も小さいのだ。
入力される曲げモーメントや材料の弾性係数はなかなか設計者によるコントロールが難しいのだが断面二次モーメントは自由である。
ここでいかに限られた場所で断面二次モーメントが大苦なる形状を考えるのが知恵の見せ所なのである。
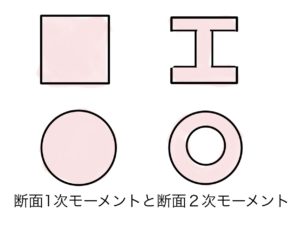
断面二次モーメントの復習はこちらをどうぞ
次に実際にたわみとたわみ角を求めてみよう。
代表的なたわみの解法(重積分法)
ここからは実際にたわみを求めて行く。最初に代表的な重積分法で解いていこう。
重積分法と名前が仰々しいが単純にたわみの微分方程式がたわみ量を2回微分しているのでそのまま2回積分を仕返して求めようというだけである。
まずたわみの微分方程式$ \frac{d^2y}{dx^2}=-\frac{M}{EI} $を一回ほどxで積分してみよう。
$ \frac{dy}{dx}=θ=-\int\frac{M}{EI}dx+C1 (C1は積分定数)$
この式はたわみ量y=f(x)を一回微分の形になりたわみ曲線の傾きを表している。たわみ曲線の傾きは物理的にはたわみの角度を表している。
そう、たわみ角がわかるのだ。ここでC1は積分定数で積分の範囲が決まってないと出てきてしまう値だ。
さらにもう一度、xで積分すると(C1のxでの積分はC1x)
$ y=\intθdx=-\int\int\frac{M}{EI}dxdx+C1x+C2 $
そう、これでたわみ量がわかる。ただしここで邪魔になってくるのが積分定数C1、C2だ。これは、とても重要なので説明しよう。
境界条件の意味(積分の超基本的な考え方)
まず積分の概念だがある関数f(x)をxで積分するということは次の面積を求めることと同意である。
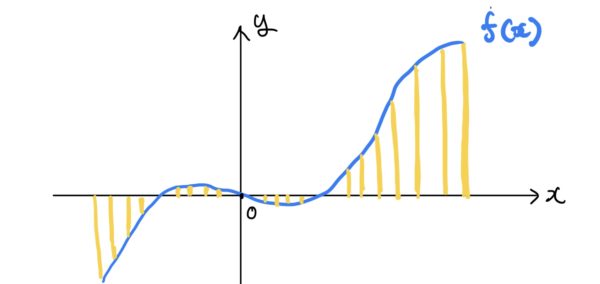
実際に積分ではどのように面積を求めているのかというと微小区間のdxとdyから面積を求めて足し合わせているだけなのだ。
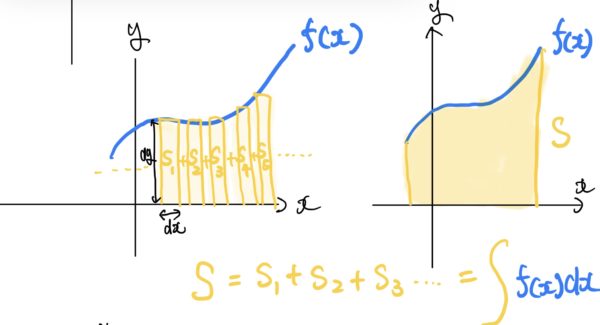
これはわかるよね。
ここからが問題で実はdxとdyの関係だけだとx=0の時のyの値がわからない。
極小区間xと極小区間yだけの関係がわかってもどこかに基準がないと絶対値、値はどんなに頑張っても求められない(多くの場合はx=0の時の値を基準にすることが多い)。
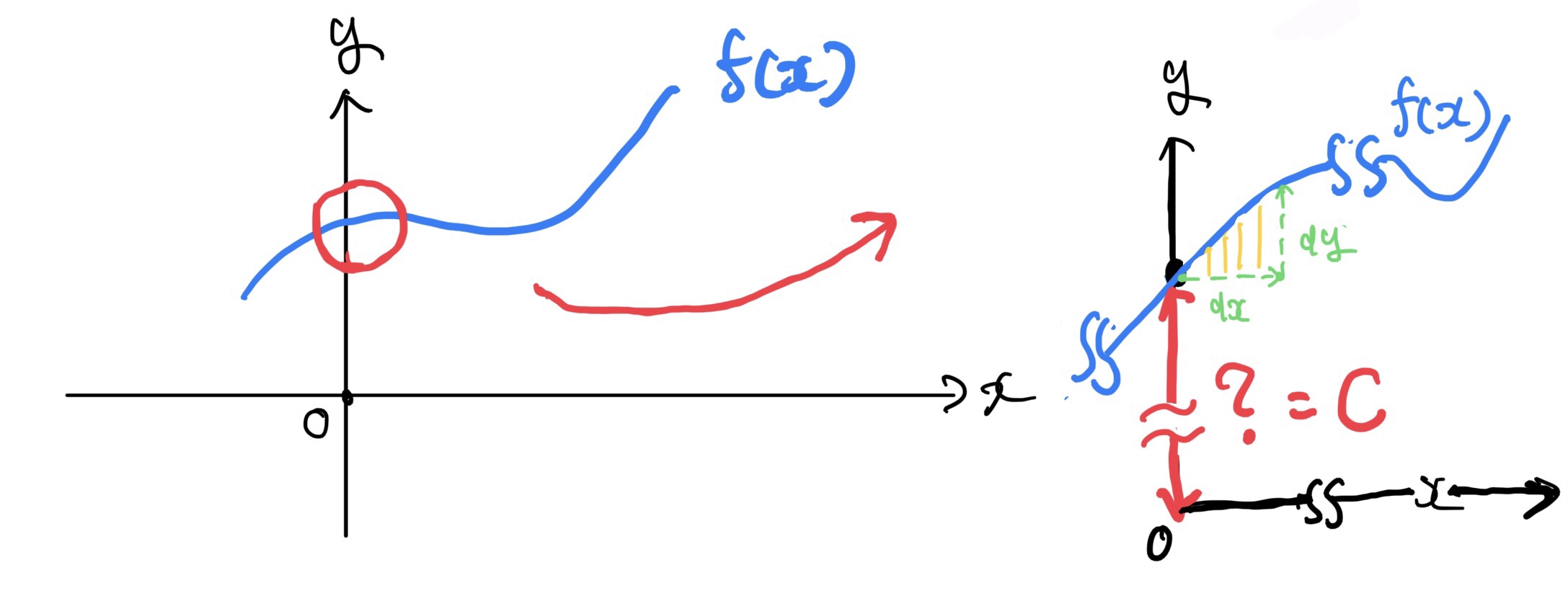
わからないのなら基準をCと置いとこうというのが積分定数だ。(数学の先生に怒られそうな雑な説明だ)
逆にCがわかれば積分の絶対値がわかる(積分定数の種類にもよるが1番の基本は、x=0の時のyの値が積分定数の値になる)。
そう、数学の世界と異なって工学の世界ではモノを測定すれば良い。
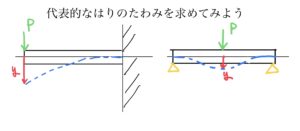
ここで例題の梁を思い出して欲しい。

これは梁の両端が物理的に固定されているのがわかると思う。端っこはどうやってもたわみ角もたわみ量も0になるのだ。
だから例題の場合のC1、C2は0になる。
このように工学における微分方程式で物理的に決まる積分定数C1、C2・・・を境界条件という。
これは、重要(たわみだけじゃない)。ただこれを決めるのが難しい。
これは機械だけでなく電気などの工学ではたくさん微分方程式が出てくる。
これら全てが境界条件を持っていてこれを間違えると全てが狂ってくる。
かの大天才、物理学者のアインシュタインでさえ特殊相対性理論で工学で言えば境界条件にあたるエーテル項を追加し、後に自分で間違いに気づき人生で一番、後悔したのは、この境界条件の間違えだったそうだ。そのくらい難しくて重要なのだ。
また今後、説明するコンピューターシミレーションも微分方程式をただ高速でたくさん解いているだけだ。境界条件は人間が入力する。
だからAIとかがどれだけ発達しても人間が決めないと計算ができないのだ。
仮に自動で境界条件を入力してくれても、それが正しいのかはAIは判断できない。
最後は人間なのだ。またリクエストがあれば工業数学講座をやるかもしれない。試験用ではなく実践のための数学だ。
まとめ
まとめ
・梁においてのたわみとたわみ角は剪断力による変形は無視し曲げモーメントによって変形する。
・梁のたわみの微分方程式は$ \frac{d^2y}{dx^2}=-\frac{M}{EI} $である。
・梁のたわみの微分方程式を解くと積分定数C1,C2という定数が出現し、これを境界条件という
・境界条件はこれから常に出現するので概念をしっかり学ぼう。
ここまでくるともう少しで設計の仕事ができるようになる。
後は座屈や疲労破壊とかの壊れ方を学べば図面の修正や簡単な部品なら設計できる。
ぶっちゃけ製図の勉強より材料力学の基礎を叩き込む方が先だと思う。
図面の表記やルールの多少の間違いは修正すれば問題ないが材料力学を使った強度計算が間違えていたらいくら製図が正しい図面でも価値なしで開発計画遅延、テスト計画やり直しに繋がり、さらには生産開始日の遅延、生産ストップ、市場でミスが発覚した場合に対応品の無償交換、最悪はリコールだ。
極端だが最悪ではこれくらいの影響が出る。
ちなみに材料力学を使わない強度計算は存在しない、さらには材料力学を使わないで作図された機械設計図面は存在しない(してはいけない)。
以上で終わりにする。
次回は、梁の微分方程式を使って代表的な梁のたわみ、たわみ角を数字で解いていく。さらに余裕があれば解法があと2種類あるので紹介したい。
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。






コメント