初心者からわかる寸法公差って何だ？（平均、分散、標準偏差、正規分布）

前回は図面の基本的な見方を説明した。今回は、図面を理解する上で不可欠な寸法公差について説明していく。

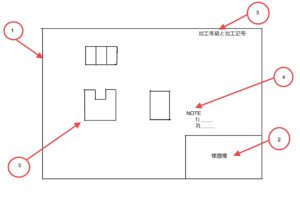
公差の仕組みを理解すれば、図面に記載された寸法公差が単なる形状のばらつきを示すだけでなく、機能や性能、さらには生産まで含めた重要な意味を持つことがわかるようになる。

本記事では、初心者でも理解できるよう、基本的に四則演算と乗数だけで説明していく。

図面の寸法公差

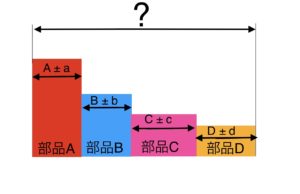
では具体的に寸法公差の記入例を見て行こう。

今回は寸法A(mm)とし公差の取り得る全てのパターンを表すと次のようになる。

通常、存在する全パターンを網羅しているはずである。

ちなみにこれからは単位mmは省略させてもらう。図面は基本的に単位はmmなのだ。

また覚えて欲しいのが寸法Aのことを称呼値(しょうこちと読む）と言う。

頻繁に使うので是非、覚えて欲しい。

基本の型はA±a（両振公差）になる。

設計上のテクニックとして、称呼値より絶対に大きくしたい場合は片振公差で0〜+a、小さくしたい場合は片振公差で-a〜0と記載する。

残りの3パターンははめあい公差などに使う(はめあい公差については専用項目で別に説明)。

形状の観点から見れば、これらは寸法に対して許容できる範囲を表している。例えば5±0.5であれば、4.5〜5.5の範囲の寸法になる。多くの方がこの意味は理解できるだろう。

ここまで普通の説明をしてきたが、生産側から図面を見ると、基本の型A±a以外の型は意味を持たず、すべてA±aの型に変換されてしまう。

造る側から見ると、この寸法の意味は加工の狙い値±許容されている誤差となる。

実際に量産する際は、さまざまな要因があって狙い値が必ず称呼値になるとは限らないが、基本的には狙い値±許容誤差としているはずである。

よって設計者も片振り公差などを使うときは、一度計算して中央値±公差の形にし、加工の狙い値を確認しておこう。

量産工程（製造現場）から見る公差の意味

量産（少なくても25個以上くらい造る）する場合は寸法公差がどう見えているかというと“加工した部品の寸法の平均値±工程での寸法のばらつき“と見ている。

ばらつきという新しい言葉が出てきたが、ばらつきの意味は単純に狙った値からどれだけ外れたかということである。

平均の意味はそのまま学校で習った平均値のことである。

例えば5という加工の狙い値として実際に造ってみたら4.6、4.8 、 5.0 、 5.2、5.4の5個ができたとする。

平均値は$ \frac{4.6+4.8+5.0+5.2+5.4}{5} $で5.0になる。

平均値と最も離れている寸法は4.6と5.4なので平均値5.0から0.4離れていることがわかる。つまり5個の部品のばらつきは最大は0.4になる。

この4個の部品の寸法の値を5.0±0.4以内と表すと図面に書かれている公差のカタチと同じになる。

よって工程の寸法のばらつき＝寸法公差と見なせるのだ（称呼値±寸法公差＝工程の寸法の平均±ばらつき）になる。

例で考えたような4個などの少数の場合は簡単だが、実際の量産となると少ないもので100個、多いと100万個を生産する場合もあるのでいちいち生産品の全部を計測して中央値、ばらつきを調べていたらキリがない（手間が掛かってしょうがない）。

ここで統計的手法を使って量産での寸法を管理する。

では例として次の表のような生産がされたとしよう。

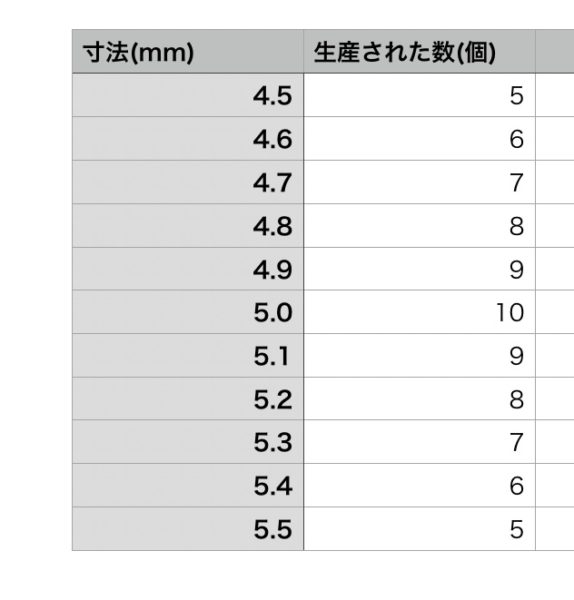
上のデータをもとに横軸を寸法、縦軸を生産された数として棒グラフを作る。

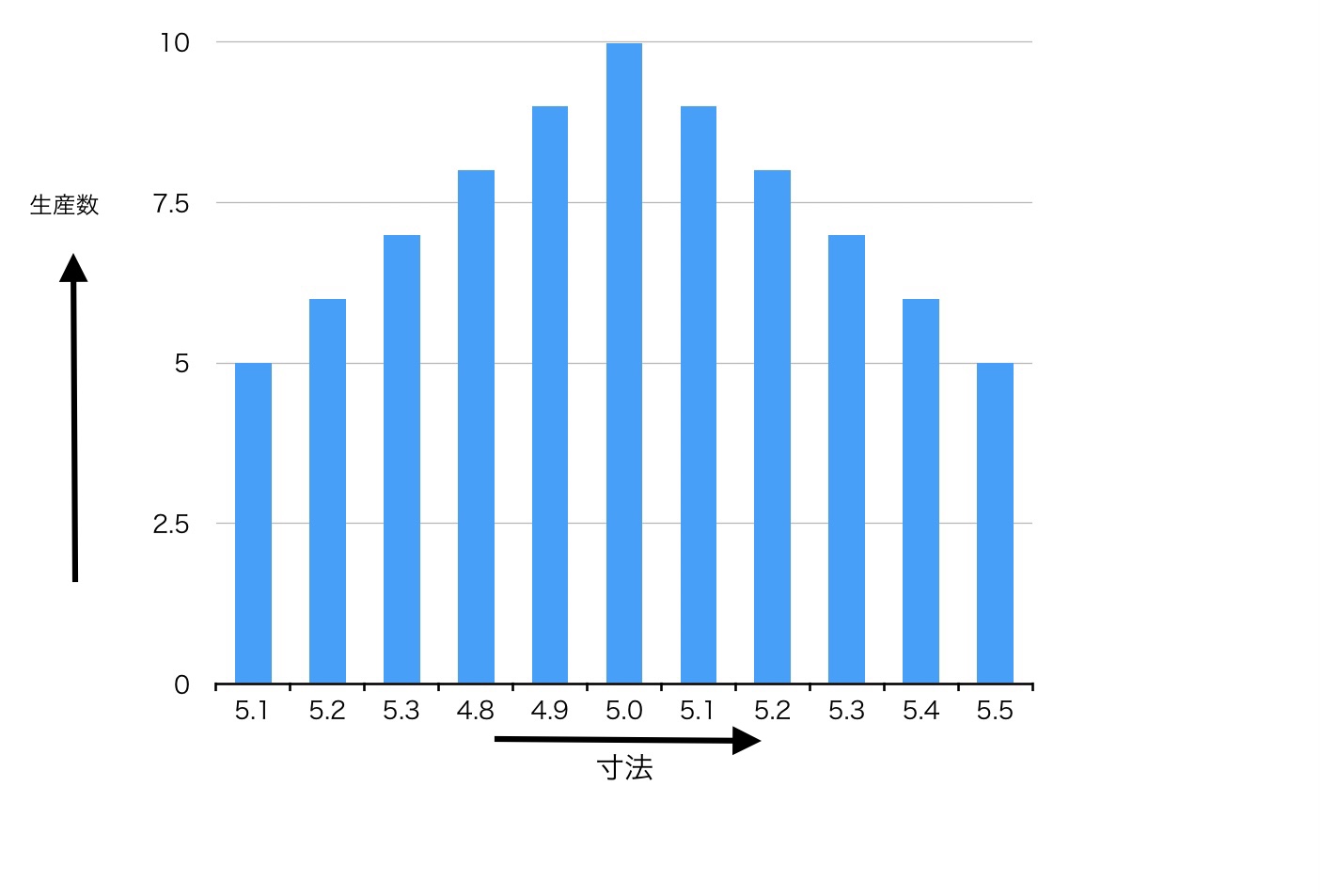
さらに棒グラフから折れ線グラフにすると

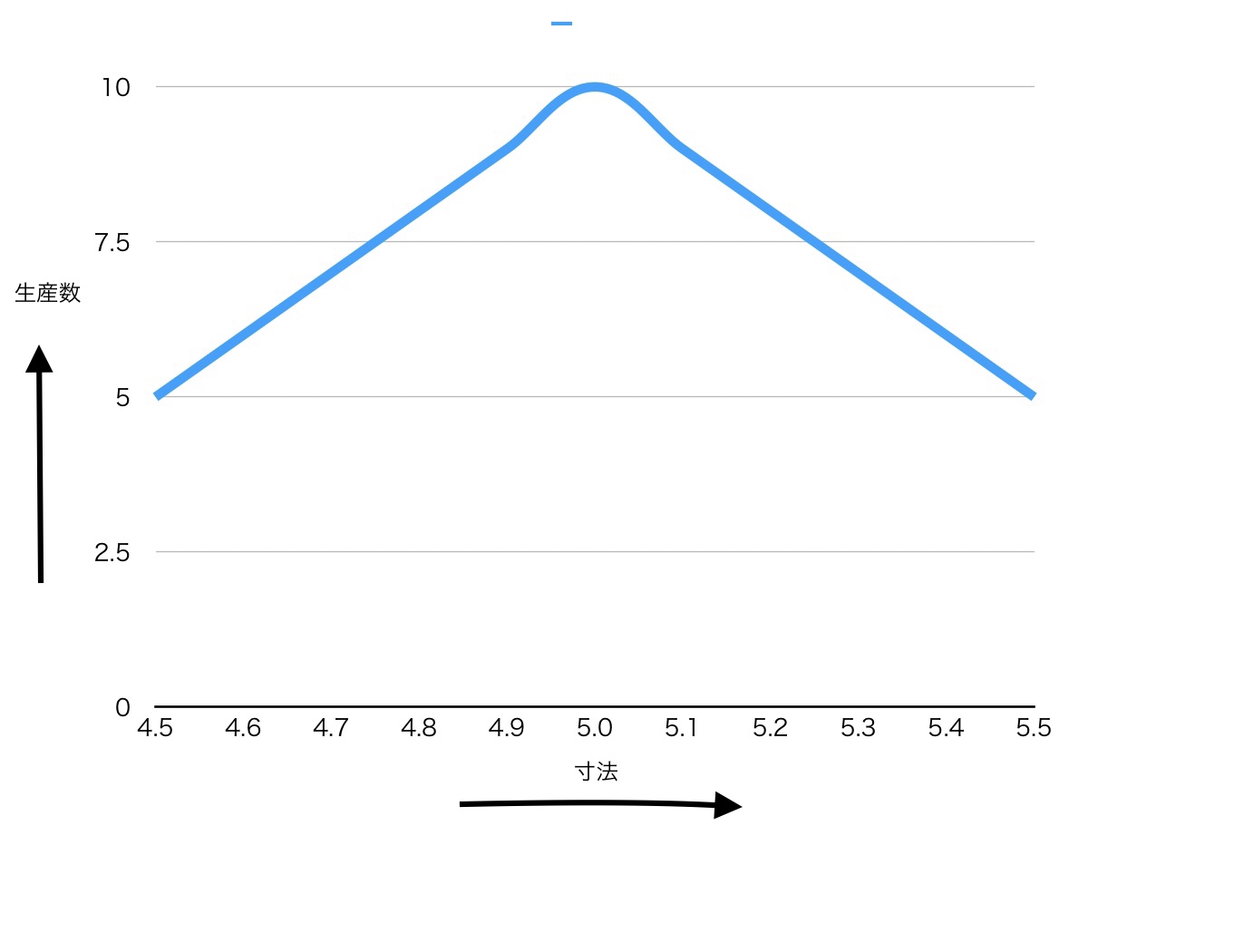
ではこの生産数をどんどん増やしていくと（例えば極端に∞個とかにする）次のようになる。

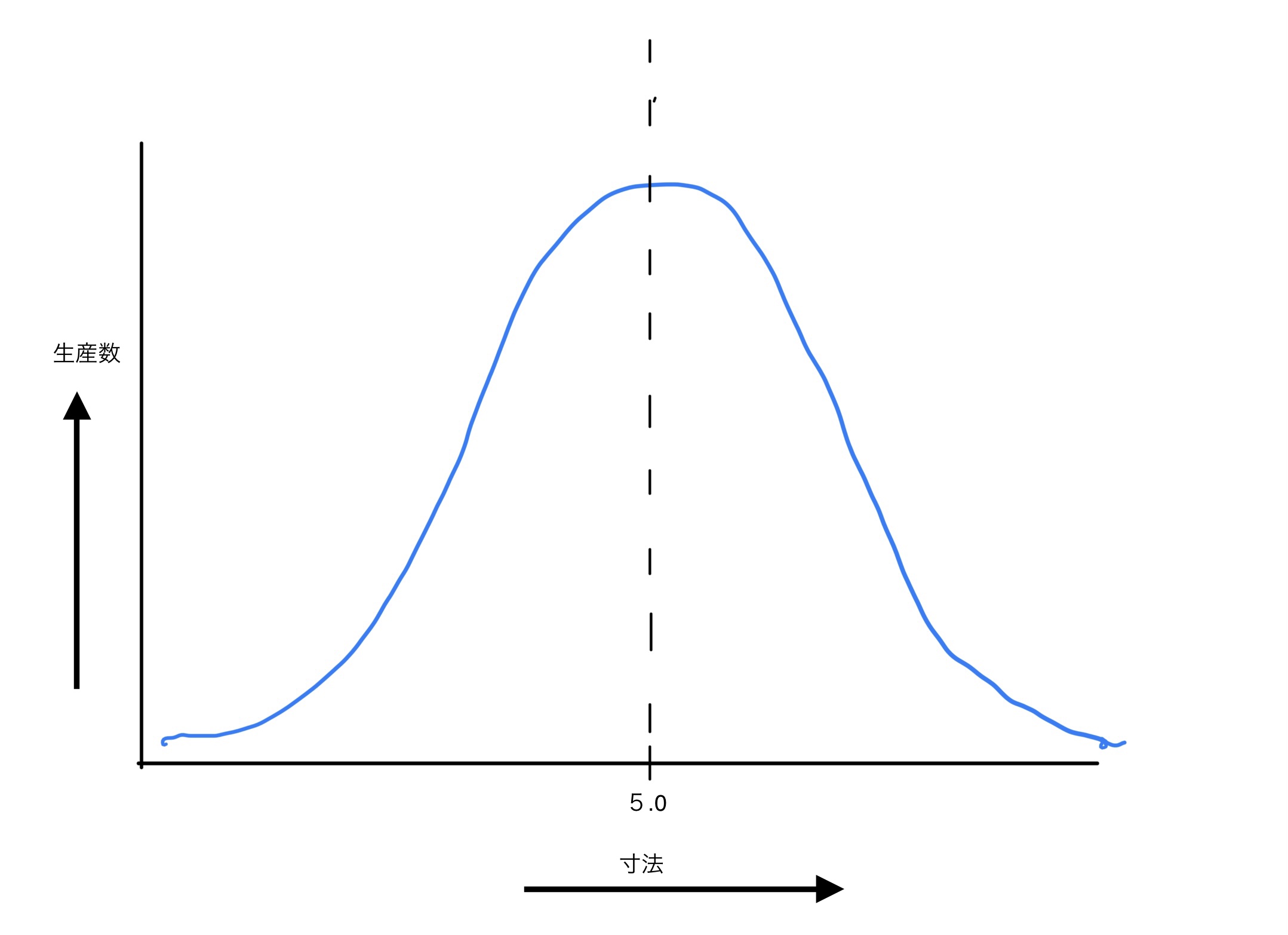
この曲線は実は統計学の正規分布という曲線になる（最近はガウス分布と呼ぶこともあるらしい）。ただし正規分布になる条件としてはしっかりと管理された工程（機械のメンテナンスなど）の場合に限る。

この正規分布になる特性を利用して、自分が関わっている部品を量産したときに寸法が正規分布を取らない場合は工程に不備があることがほとんどのパターンだ（生産技術的に無理なパターンもある）。

従って量産品に不良が多く出た場合は生産した部品の寸法を計測し横軸を寸法、縦軸を生産数のグラフを作成して分布を確かめることをお勧めする（分布の検定）。

もしグラフが正規分布に従っている場合は無理な寸法の振り方をしていることが多いので図面（公差）を見直すか必要に応じて工程の改善をする必要がある（工程改善はコスト高に繋がることが多いので注意）。

この正規分布は非常に便利で、生産した部品の平均値とばらつきの度合いが分かれば不良寸法が工程で何％の確率で発生するのかが簡単にわかってしまう。

正規分布について

管理された量産工程で生産される部品の寸法が正規分布の形になることを理解した上で、実際に“どんな数字がわかれば正規分布を書けるのか“を説明しよう。

まず一つ目の数字は生産された部品の寸法の平均値μ（ミューと呼ぶ)が必要。

μの求め方はn個の場合は$ μ=\frac{a+b+c}{n} $(a,b,c・・はn個まで続く）

2つ目に必要な数字はばらつき度合いを示す尺度である分散$ s^2 $(エスの2乗）が必要。

ただし分散と聞いて難しいと思わないで欲しい、以下の単純な計算の結果を分散というだけである。

n個の部品の寸法の分散$ s^2=\frac{(a-μ)^2+(b-μ)^2+(c-μ)^2}{n} $(上辺のa、b、c、・・・・はn個まで続く）

ちょっとかっこよくまとめると$ s^2=\frac{Σ(x-μ)^2}{n} $と表される。

統計の理論では分散を求める際にn-1で割るが、nが多いと誤差が小さいので量産が前提の工業では問題にならないことが多いのでｎで割ることが多い（扱うn数が30個レベルだとnとn-1の誤差が3.4%程度、もし理論が気になる下のリンクへどうぞ）。

Σ（ラージシグマ）はただ単に”カッコの中の式をn回足してくれ”という意味なだけである。

ここで出てくる疑問は“なんで分散は平均と差分した2乗の値を取り扱うのか“だと思う。

ばらつきを表すのに2乗の計算を行うことは非常に重要なことなので詳しく説明する。

そのまま単純にばらつきを考えると、例えば平均が5に対し値が5.1だとばらつきは＋0.1、４.9の場合だとばらつきは-0.1になるのでばらつきを足し合わせる0になってしまう（本来はばらつきは存在する）。

一方でばらつきを2乗しておけば5.1のばらつきは$+0.1^2$、4.9のばらつきは$-0.1^2$で足し合わせると$0.01+0.01=0.02$で平方根を取ると$ \sqrt{0.02^2}=0.014 $となりちゃんと加算され正確なばらつきが表現できる。

もう一つ重要な値が標準偏差σ（シグマ）である。

これも難しく考えないで以下の式が標準偏差というものなんだと覚えて欲しい。

標準偏差$ σ=\sqrt{s^2} $

これだけである。

平均μと分散$ s^2 $と標準偏差σがわかれば次のような正規分布が決まる(EXCELなどで書ける、昔ながらのアナログなやり方だと正規分布表を見て書く）。

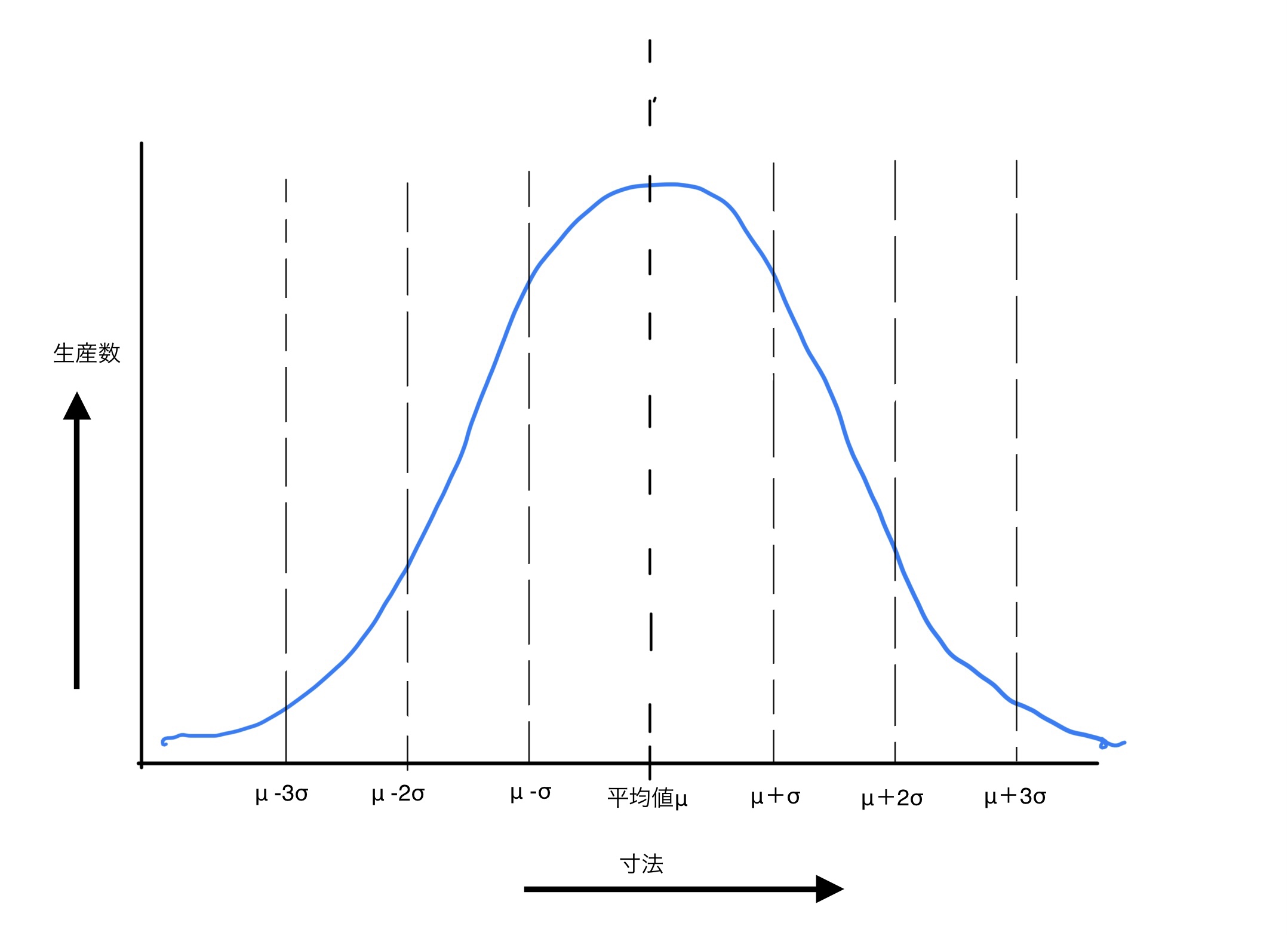
見て解るように標準偏差の値が大きくなるほどそれぞれの寸法の生産数は減っていく。

このような正規分布を$ N(μ,σ^2) $と表す。

この正規分布の優れているところ正規分布に従うのであればμ -σ~μ+σの間の寸法を取る確率は68.2%であると決まってしまうのだ。

さらに2σ以内では95.4%、3σ以内では99.7％（1000個に3つで覚える）の確率で存在すると決まるのだ。

これこそ人類が創造した英知と言ってもいいと思う。

実際に考えてみると正規分布に従う工程であればどんだけ多くの数（極端に∞でも良い）を生産しても平均と分散がわかればどのくらいの割合（確率）でどんな寸法が出来上がるのかがわかってしまうということだ。

例えばある工程で平均が5で分散が0.1だとしよう。標準偏差は分散の平方根なので電卓を叩いて約0.316だ。

そうすると例えばμ±3σを計算すると４.05〜5.95になり、この工程で4.05~5.95の範囲の寸法で生産される確率は99.7％である。

言い方を変えれば“1000個に3個以外はこの寸法を保障します“ということなので1000個の生産で997個、1万個だと9970個が4.05~5.95の範囲で必ず生産される。これは何億個作っても変わらない割合なのだ。

つまり生産が正規分布に従う限り、生産される寸法のばらつきの発生確率は100％完全に把握できるのだ。

ここまでのことから読者の多くの方はお気付きだと思うが、生産が正規分布に従う場合、寸法は決まった確率で平均μー標準偏差σ〜平均μ＋標準偏差σの範囲に収まる、書き換えると平均μ±標準偏差σと書ける。

そう、ここで記事の中の布石が繋がってくるのだ。

つまり寸法公差は工程の寸法のばらつき、標準偏差そのものになる。

ここまでで“平均と分散がわかれば生産される寸法が解る“ということが理解されたところで”実際にいくつくらいの生産数でど平均、分散を求めればいいのか？”という疑問が湧くと思う。

平均、分散を求める具体的な生産数は各企業、団体や考え方で異なってくるのだが筆者は30個程度の平均、分散を取れば正規分布に従うと考えている（最低で25個）。

理由は何個の部品の生産数で無限に正規分布に従うのかを考えるのと信頼度区間とか中心極限定理の理論からおおよその生産数が見えてくる（別記事で詳しく解説する）。

それを見ていくと数を30個を跨ぐ付近で急激に正規分布に従い始めて30個以降はあまり変わらなくなる。

この性質を使って基本は30としている（実際の現場だと25～30個が多い）。
※1ロットの生産数を30個程度にする理由も、この正規分布が大きく関わっている

要するに“30以上の部品で平均、分散を取ればより正規分布に近づくけど、25以上30未満と対して変わりませんよ“ということだ。

ここら辺の正確性はコストと精度とのトレードオフになる。

平均と分散を求める際に取り扱う部品の数が少なければ安く済むけどバラツキは大きい、部品の数を多くすればコストは上がるけどバラツキは減る。バランスが大切なのだ。

まとめ

ここまでをまとめる。

次回は寸法公差のばらつきをσを使ってどのように設定するかを工程能力という数字を使って解説していく。

この記事が「設計の理解」に少しでも役立ったと感じた方へ

折角なので機械設計で必須の本があるので紹介します。

はっきり言って中身は不親切極まりないのですが細かいことをちょっと忘れた時に辞書みたいに使えます。この記事を見てくれれば内容が理解できるようになって使いこなせるはです。またよく使う規格も載っているのでかなり重宝します。

持っていない人はちょっとお値段が高いのですが是非、手に入れて欲しいと思います。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメします。