l前回までで材料力学の破壊まで説明して一通りの材料力学の全体を説明してきた。
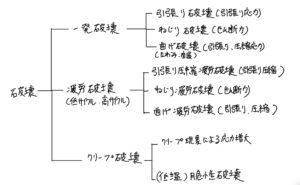
特に考え方に重点を置いて説明してきたつもりだ。
今回からは、少しだけ特殊な解き方をしないと解けな応力の問題の解き方を説明していく。
特に微分積分や微分方程式を解かないと応力がわからない問題を取り扱う。
しかしながら別に難しいことはなく、あくまで大切なことは考え方であって式の処理はおまけである。
いつもながらのセリフだが暗記をするのではなく、“特殊な解き方の問題があるんだな“と認識をしてもらって,使うときに思い出して見返せば良いと思う。
では説明していこう。
棒の自重による変形
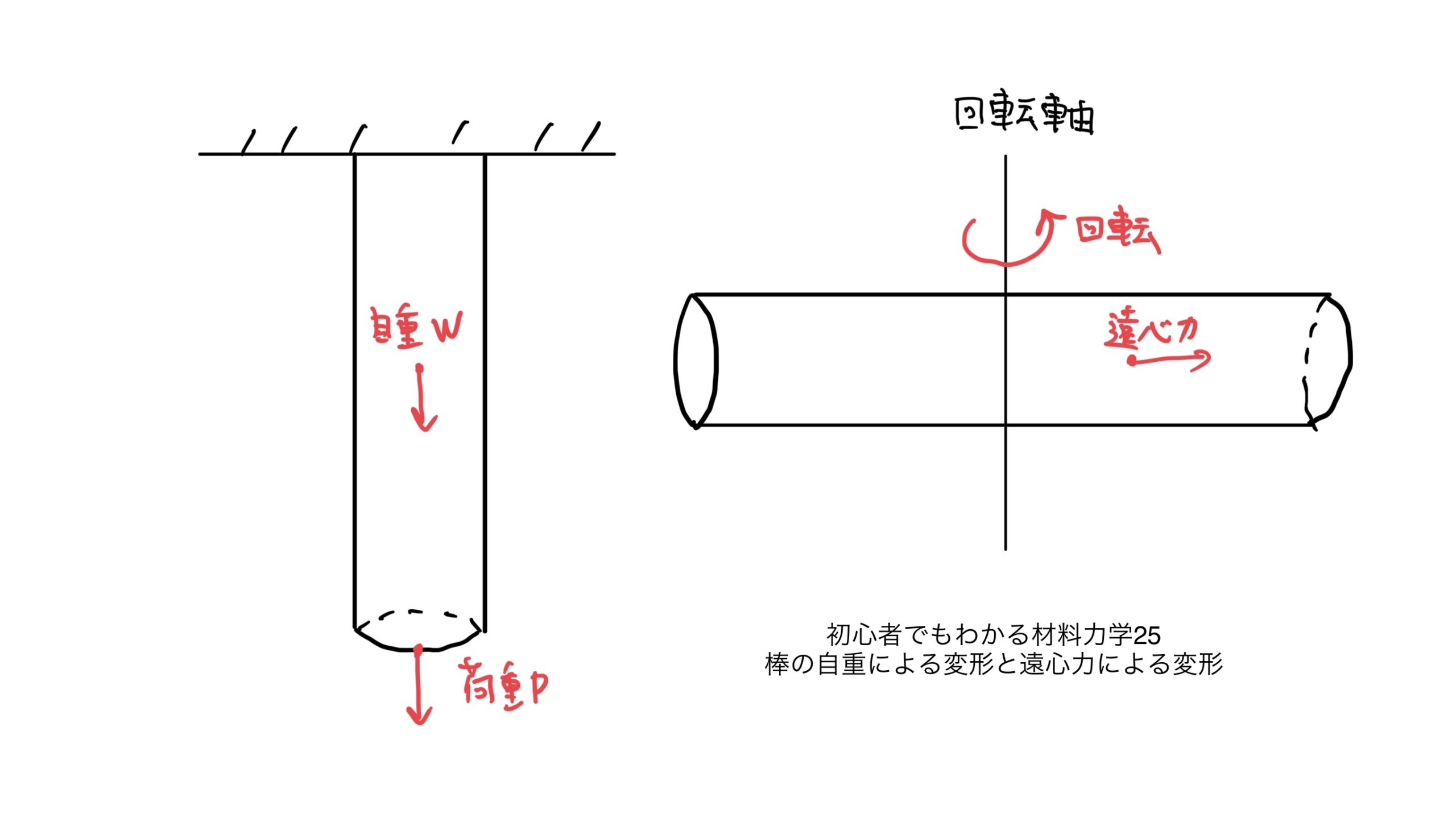
今回、考えていくのはかなり長い棒(断面形状が円で一定)が天井から吊るされている場合に自分の重さによって発生する応力を考えていこう。
今までは、部材の重さは外力に対してかなり小さいものとして無視してきたがここでは自重の影響を考慮して考えていこう。
いつもながら例題を考えると棒は、長さLで断面積Aで密度がρ$[kg/m^3]$で重力加速度がg$[m/s^2]$で先端に荷重Pが発生している場合を考えていこう。

まず単純に外力の釣り合いを考えると次のようになる。
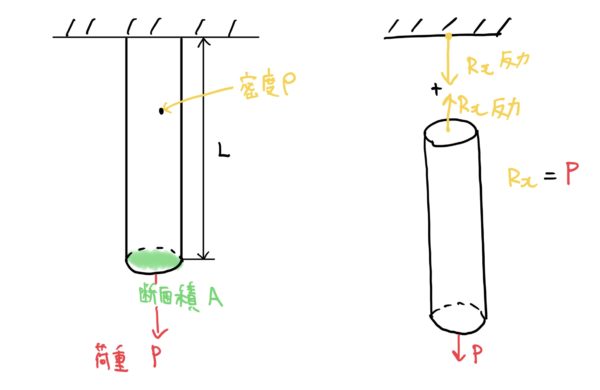
これは高校物理の基本になる。
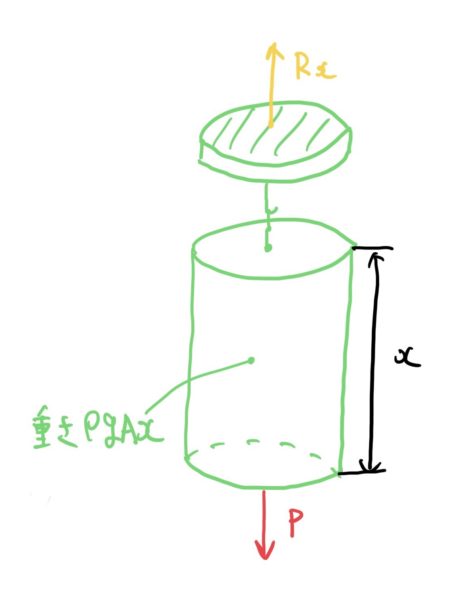
ここからが少し特殊な考え方で、まず棒に先端を0、天井をLとする座標を与えてある座標xでの棒の微小区間dxでの力の釣り合いを考えてみよう。

そうすると力の釣り合いの式は次のようになる。
$ Rx=P+ρgAx(密度×体積) $
つまり、ある座標地点xにかかる外力は、荷重Pに加えx地点までの棒の重さが掛かることになるのだ。
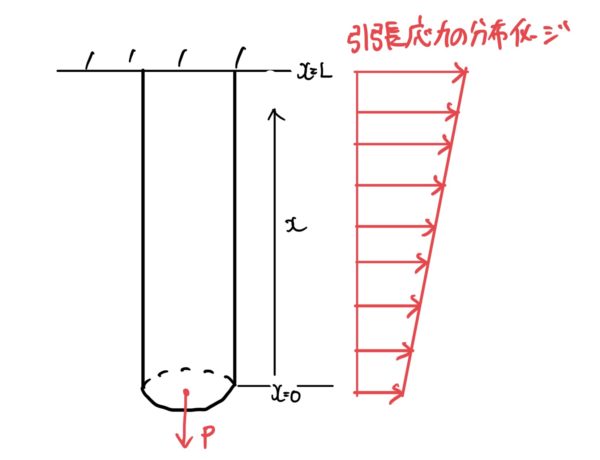
よって応力は、次の式で表される。
$ σx=\frac{P+ρgAx}{A} =\frac{P}{A}+ρgAx $
この式から棒に発生する応力の最大は、xがLの時、つまり天井に吊り下がっている場所で次の大きさになる。
$ σmax=\frac{P}{A}+ρgAL $
ここでσmaxを材料の降伏応力σaとして棒に必要な断面積を考えていくと次の式に変形できる。
$ A=\frac{P}{σa-ρgx} $
となり、棒が吊るされている根本に近づけば近づくほど必要な断面積は太くなるのだ。
当たり前だが降伏応力σaがρgxが最大となるLのρgLと同じ大きさだと必要な断面積は∞となり事実上、成り立たないのだ。
次に棒の伸びを考えていく。
伸びをλとして考えるのだが、ここでも少し特殊に考えである座標地点xでの微小区間dxの伸びdλを考える。
歪みをε、材料の弾性係数をEと置くと
$ εdx=dλ、ε=\frac{dλ}{dx}=\frac{σx}{E} $
よって微小区間の伸びdλは、次式でまとめられる。
$ dλ=\frac{σx}{E}dx=\frac{1}{E}(\frac{P}{A}+ρgx)dx $
となり、これを座標0からLまで積分すれば伸び全体の伸びλが求まる。
$ λ=\int{dλ} =\frac{1}{E}\int_0^L{(\frac{P}{A}+ρgx)}dx=\frac{PL}{AE}+\frac{ρgL^2}{2E} $
伸びλを縦軸、横軸を棒の長さとすると次のようなグラフになる。
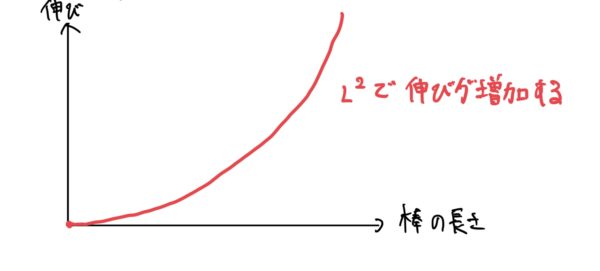
となる。
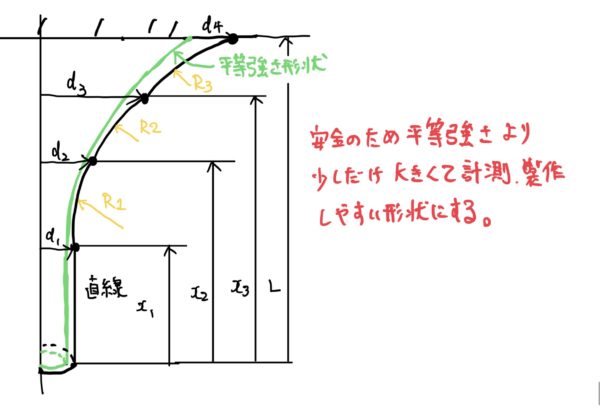
平等強さの棒
ここまでの説明で侍従の影響を受ける棒は、座標によって発生する応力が異なることが理解できたと思う。
特に根本に近づくほど発生する応力は、かなり大きいくなるのだ。
つまり断面積が同じ棒は、長くなればなるほど根本の必要な断面積が大きくなり全体としてかなり太くなってしまいコスト面や重量面からかなり無駄の多い設計になってしまう。
そこで断面積を座標によって可変させて各座標で必要最低限の断面積にすると棒はかなり軽くなるのがわかると思う。
このように棒に生じる応力が全体で等しくなるような棒を平等強さの棒と呼び工業で使用されることがとても多い。
ではどんな断面積変化をすると平等強さの棒になるのかを求めていく。
まず例題を考えると断面積が変化する長さLの棒の先端に荷重Pが作用している。
密度は、ρで重力加速度はgとし座標の置き方は上と同じように考える。
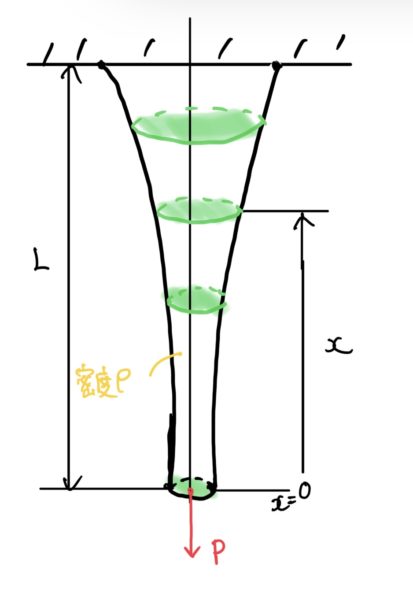
ここで、また特殊な考え方になるのだがある座標xとx+dxにおける断面積をそれぞれA、A+dAとする。
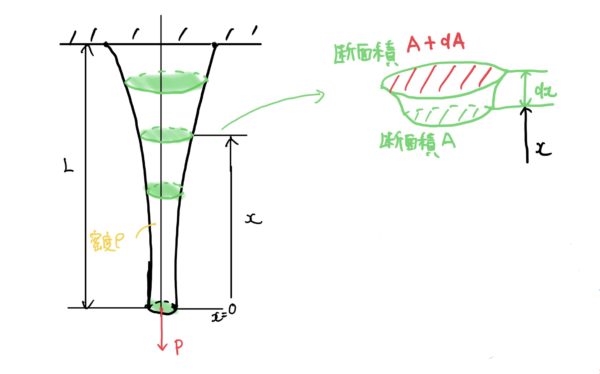
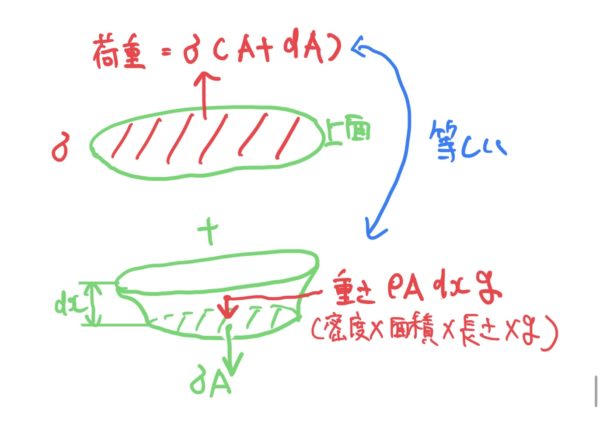
この時に平等強さの棒にしたいので座標xで発生する応力と座標x+dxで発生する応力を等しくすると次の式が成り立つ(発生応力をσと置く)。
$ (A+dA)σ=Aσ+ρgAdx(dx間に作用する自重) $
$ \frac{dA}{A}=\frac{ρg}{σ}dx $
これは微分方程式と呼ばれる式で取り敢えず解いてしまうと次のようになる(C`,Cは積分定数)。
$ \log A=\frac{ρg}{σ}x+C`. A=Ce^{(\frac{ρg}{σ}x)} $
積分定数を求める境界条件は、棒の最下端の断面積をA0とすればx=0でC=A0=$\frac{P}{σ}$となるの平等強さの棒の断面積の式は、次のようになる。
$ A=A0e^{(\frac{ρg}{σ})x}=\frac{P}{σ}e^{(\frac{ρg}{σ})x} $
となる。
つまり外力Pと棒の最下端の断面積A0が決まれば棒全体の形状が決まるのだ。
さらに伸びは、簡単で全伸びλは、応力が全体で等しいので
$ λ=\frac{σ}{E}L $
となる。
よって平等強さの棒の形状は次のようになる。

実際には断面積が自然対数eの乗数になるよう厳密にすると図面指示や製造、検査がかなり大変になるので平等強さの棒の形状に近くなるようにする。
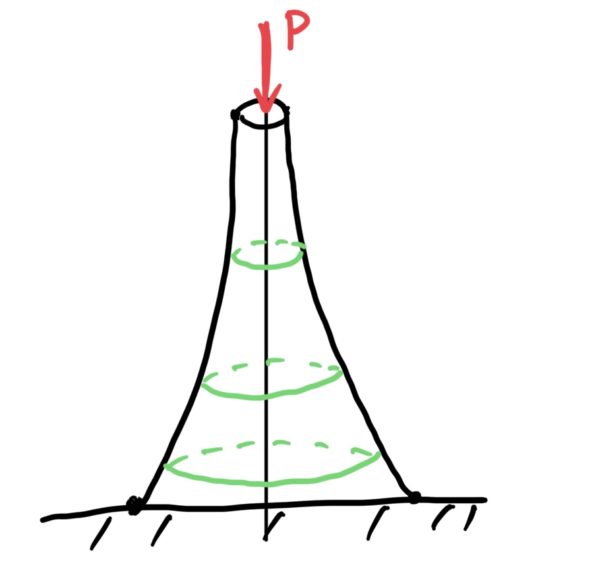
ここまで棒の侍従による引張り荷重を中心に説明してきたが、棒を立てた場合の圧縮でも同じ考えが成り立ち結果の式は符合が逆転するだけである。
この考えから東京タワーやスカイツリーなどの巨大建築物などの自重による影響が大きいのでよく見ると平等強さの棒のような形状になっている。
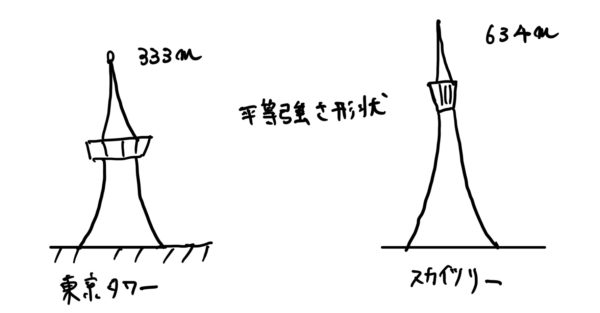
良かったら検索でもして外観形状を見てみて欲しい。
実際に機械においては、筆者の専門の自動車エンジン程度の大きさだと構造部材の重さに対して外力が圧倒的に大きいことが多くてあまり使うことはないが“こんなのがあったな“と気に留めておいて欲しい(建築や設置型の大型機械、船などでは、よく使うと思う)。
また本稿は、数学の説明を省いているが今後の予定で数学の講座も開設するので微分、積分、微分方程式、対数などの説明は、今後に期待して欲しい。
遠心力を受ける物体の応力
次に遠心力による応力の発生を考えていこう。
これはどんな機械でも超重要で回転する機械要素は、かなり多く使われているので是非、理解しておこう。
まずはイメージを掴むために簡単な例題で考える。
例題は、ある軸から距離Lだけ離れた位置に質量mの物体が角速度ω[rad/s]で回転しているとする。
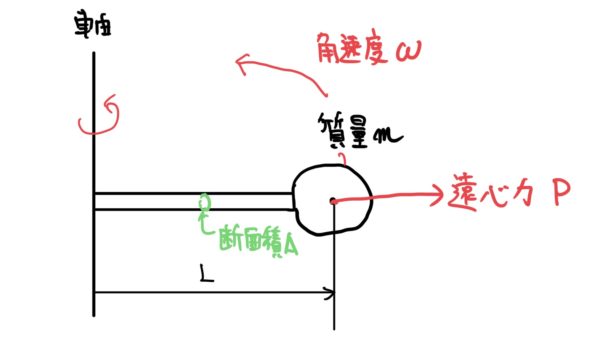
質量mを軸と繋いでいる棒の質量を無視して断面積をAとすると棒に発生する応力σは次のようになる。
$ 質量mによる遠心力P=mLω^2 $
$ 発生応力σ=\frac{P}{A}=\frac{WL}{A}ω^2 $
となる。
このような遠心力、慣性力や上で説明した自重などの質量に比例して物体内部に作用する外力を物体力と呼ぶ。
この物体力が働く場合の応力の解き方は、自重の影響と同じように座標を取って微小区間の力の釣り合いを求めて積分したり微分方程式を解くことが多いので頭に留めておこう。
次に自重による遠心力が物体に作用する場合を考えていく。
まず例題を設定すると全長2Lの一様な断面(断面積A)を持つ棒が中心Oで棒に対して垂直な軸を回転軸とし角速度ωで回転している場合を考えよう。
ここで棒の半分の伸びをλ、密度をρとする。

物体力によって発生する応力なのでいつものことながら回転軸Oを座標原点とし先端に向かって+とするx座標を設置する。
次に回転軸から距離ξ(クサイ)だけ離れた微小区間dξに質量ρAdξ(密度×断面積×長さ)の遠心力dPは次に式で表される。
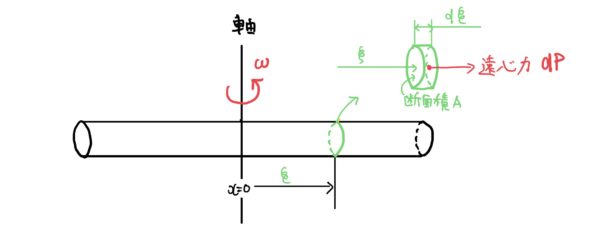
$ dP=ρAdξ・ξω^2(回転半径×角速度の2乗) $
ここから回転軸からとある距離xに発生する引張り力Pxはξがx~Lまでの各微小区間によって発生する遠心力の足し合わせなので次のような積分を行う。
$ Px=\int {dP}=\int_x^L{ρAω^2ξ}dξ=\frac{ρAω^2}{2}(L^2-x^2) $
となるので応力は断面積がAなので次式になる。
$ σx=\frac{Px}{A}=\frac{ρω^2}{2}(L^2-x^2) $
これより回転する棒の遠心力によって発生する最大応力は回転軸Oのx=0の場所で
$ σx=\frac{ρω^2L^2}{2}$
となる。
また棒の伸びλは、微小長さdx部分の伸びεdx=dλ、ε=Eσxより$ dλ=\frac{σx}{E}dx $になるのでσxに上式を代入してxが0からLまでの積分をすれば求まる。
$ λ=\int {dλ}=\int_0^L{\frac{σx}{E}}dx=\int_0^L{\frac{ρω^2}{2E}(L^2-x^2)}dx=\frac{ρω^2}{2E}\displaystyle\left[L^2x-\frac{x^3}{3}\right]_0^L=\frac{ρω^2L^3}{3E} $
となる。
ここまでは中心(x=0)から片方の端部(x=L)までの伸びλを求めただけなので棒全体の伸び(棒の全長は2L)は倍の$ \frac{2ρω^2L^3}{3E} $となる。
ここで面白い特性なのが回転する物体の発生する応力、伸びのともに断面積は一切、関係なく密度と長さと回転数(伸びは弾性係数も関係する)で決まってしまうのだ。
つまり回転する物体の応力は、物体が棒だろうが円だろうがギヤだろうが形状に寄らなくて物体の材料(弾性係数、密度)と大きさ(半径)と回転数で決まる。
また発生応力の式$ σx=\frac{ρω^2}{2}(L^2-x^2) $をグラフに表すと次のようになる。
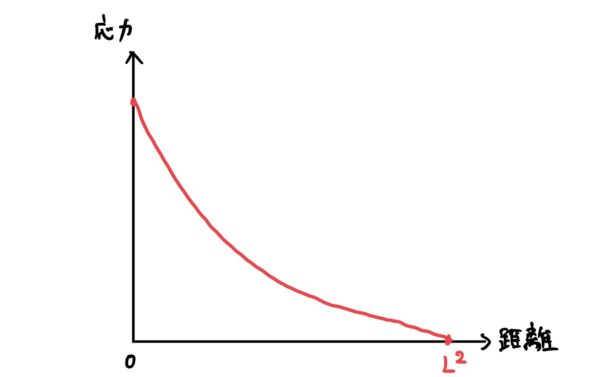
当たり前だが回転軸からの距離の二乗で応力が減少していくので回転する物体の設計をする時には、回転軸廻りにたっぷりと肉をつけないと壊れる。
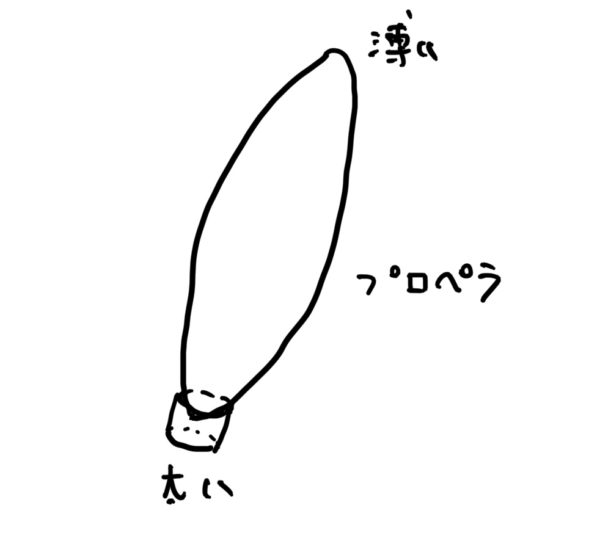
この代表的な機械だと飛行機やヘリコプターのプロペラが典型例でよく見ると根本にはたっぷりと肉が付いており、先端に行くほど薄い形状になっている。
だから自動車のフライホイール(慣性力維持装置)やギヤ、バランサーなどの軽量化をする場合は、回転軸廻りは肉を残して、あとはごっそりと肉を抜いても大丈夫だ。
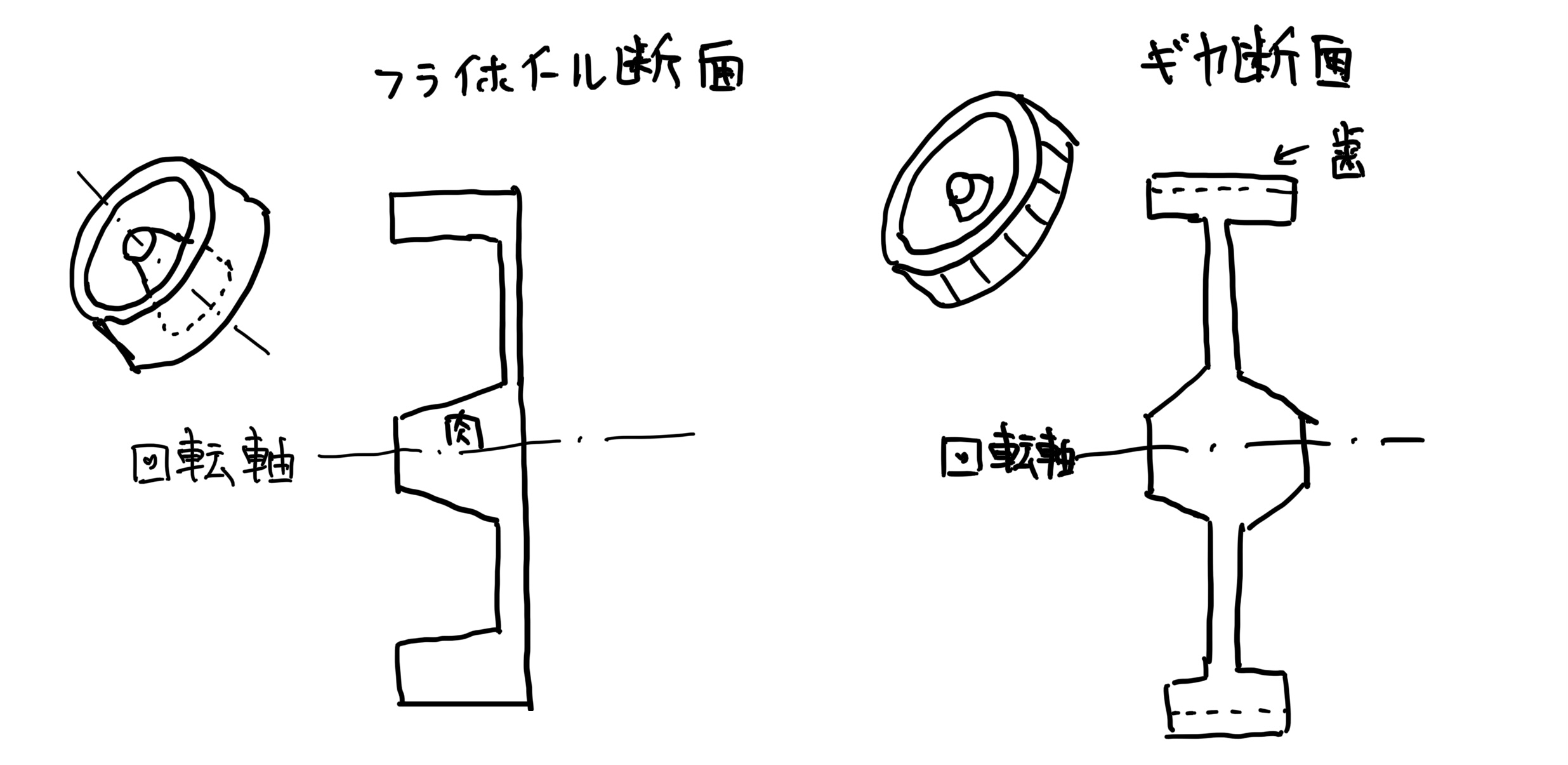
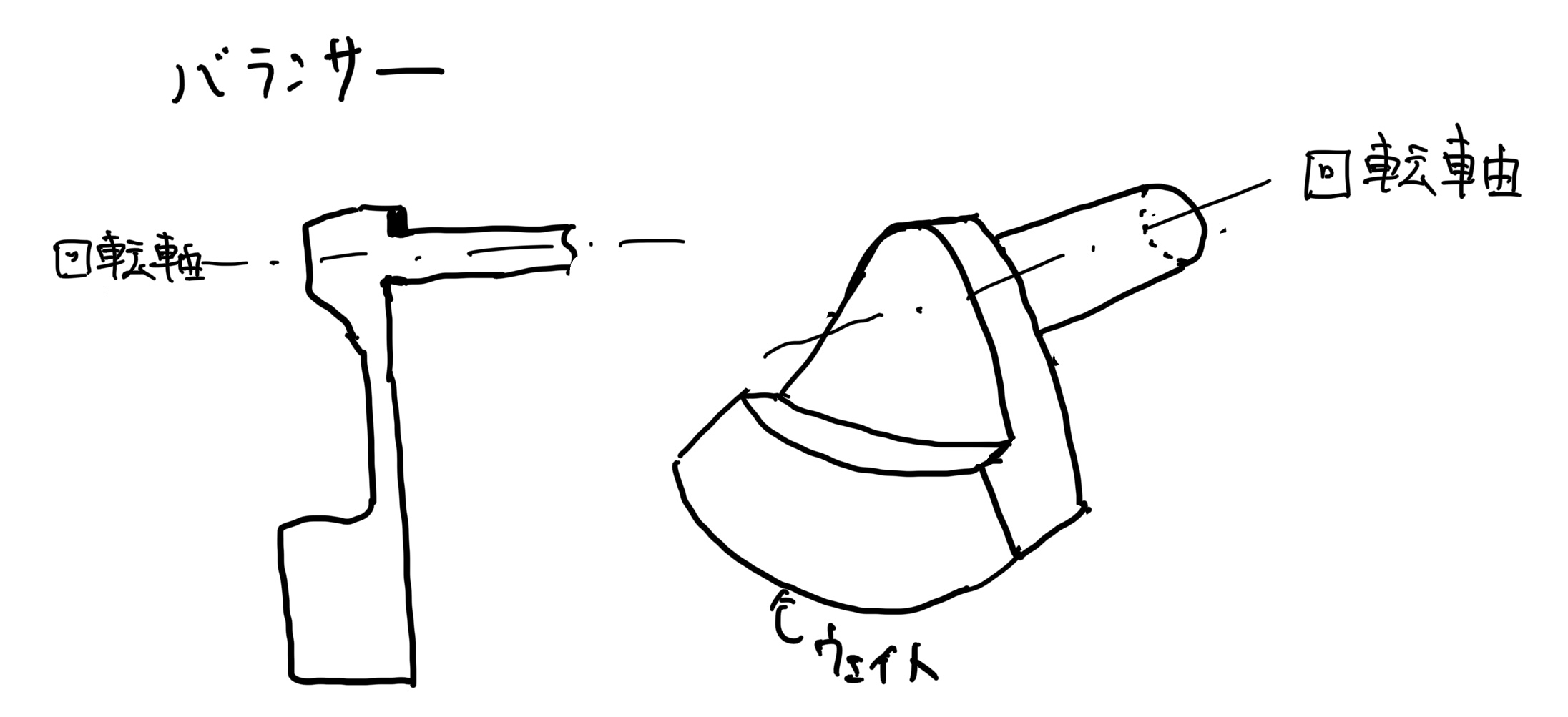
ただしフライホイールのような慣性マスを維持する装置は、回転物体の先端に質量が集中しているので回転軸廻りに十分な肉厚を残しておこう。
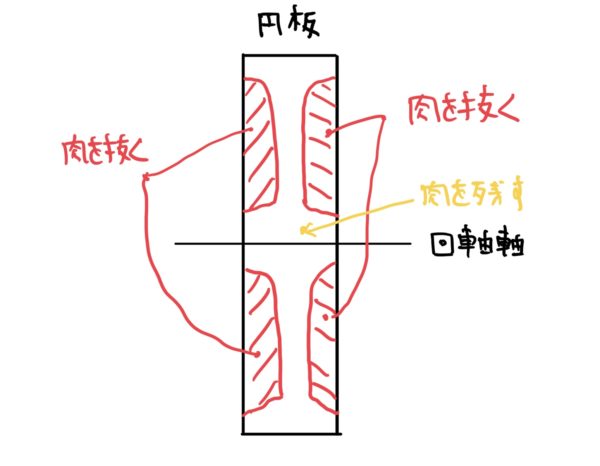
また式からわかるように遠心力は回転数の2乗に比例して増大するので増速ギヤ(例えばエンジンの2次バランサーなど)などの回転数が高くなる場合に関しても回転軸廻りの肉厚は十分に確保しないと破壊する。
とにかく回転する物体の応力は、距離の二乗で減少し回転数の2乗で増加する関係は、頭に入れておくと便利だ。
以上で今回の説明を終わりにする。
次回は、単純な球型の圧力容器と円筒型の圧力容器に発生する応力の説明をする。
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。





コメント
コメント一覧 (2件)
回転棒、伸び倍じゃないですか?
にに様
コメントありがとうございます。
ご指摘、ありがとうございます。棒全体(2L)だと伸びλは倍になりますね。