本ブログでかなり昔になりますが”初心者からわかる寸法公差”という記事で平均、分散、標準偏差、正規分布を説明しました。

リンク先の記事の中では分散を求める際に
- $ s^2=\frac{(a-μ)^2+(b-μ)^2+(c-μ)^2}{n} $(上辺のa、b、c、・・・・はn個まで続く)、まとめると$$ s^2=\frac{Σ(x-μ)^2}{n} $$で表される。
- 統計の理論では分散を求める際にn-1を使うが、nが多いと誤差が小さいので量産が前提の工業では問題にならないことが多いのでnで割ることが多い(扱うn数が30個レベルだと分散の差が3.4%程度)
と説明させて頂きました。
今回は公差の記事で説明を省いていた分散を求める際のn、n-1の違い、意味を詳しく説明していきます。
Kazubara blogらしく厳密な数学の証明よりは、エンジニアがよく直面する問題の生産品質と絡めてイメージで掴めるような解説にしています。
平均、標準偏差、分散のおさらい
本ブログは機械設計、工業を主に解説しているサイトなので工場、製作所で生産された部品寸法のバラツキを例に解説していきます(別に人の身長でも体重とか何でもいいです、興味がある人はサンプルの数字を作って倣って計算してみて下さい)。
まずは平均のおさらいからしていきましょう。
例えば製作所の工程で生産された部品の寸法の狙い値が5.00だったとします。しかし生産された部品の寸法は狙い値から外れて行くので実際には5.00になることは稀です。
最初に製作した5個の部品の寸法がたまたま4.68, 4.82, 4.88, 5.02, 5.10だったとしましょう(5個の生産でたまたま完成した寸法)。

この時の平均寸法は小学校で習った平均と同じで(平均を$\bar{x}$としましょう)
になります。
ちょっとかっこつけて数学っぽく書くと次のように表せます。

次にそれぞればらばらだった寸法のバラツキの表し方を考えてみましょう。
もっとも簡単な方法は各寸法と平均$\bar {x}$の差ですね(各寸法-平均$\bar {x}$)。
ここで各寸法のばらつき5個が算出できましたが、このままでは各ばらつきが扱いにくいままです。特に困るのが+とーが混ざっています。
+と-が邪魔なのでそれぞれの5個のばらつきを二乗します。
このままだとただの5つの数字なので5個の平均を取りましょう。
これを分散と呼び、一般的に$S^2$で表されます。
各ばらつきを数学っぽく表すと$(x_i – \bar {x})^2 $なので、分散は以下の式で表せます。

これで生産された任意のn数のばらつきの平均値がわかるようになります(二乗していることに注意)。
この分散$S^2$を平方根した数字を標準偏差σと呼びます(標準偏差はばらつきと同じ次元数なので同列に扱える)。

ややこしいですが分散は$σ^2$で表されることもあります。
ここで平均、分散、標準偏差が求められると工場で生産された全部の部品の寸法のばらつきが判明します(生産された部品の寸法が正規分布に従う場合、まともな工場なら正規分布に従う)。
※正規分布はガウス分布、ベルカーブとも呼ばれる。詳しい解説は別途しますのでふ~んくらいで大丈夫です。
求められた平均(4.90)、分散($0.022$)、標準偏差(0.15)で度数分布表を使うと以下のような正規分布が書けます(下の図は筆者が表計算で作成)。

この分布をN(平均μ、標準偏差$σ^2$)と表すので今回の例ではN(4.90、$0.015$)と表せます。
この正規分布の凄い性質は各寸法のバラツキがどのくらいの割合で発生するかが完全にわかってしまうことです。

つまり例に挙げた5個寸法だと平均:4.90、標準偏差:0.22なので4.97±0.22が存在する確率は68.2%、4.90±0.044が存在する確率は95.4%とわかってしまいます。
だからこそ平均、分散、標準偏差は非常に重要な数字になります。
分散の分母n、n-1について
ここからが本記事の本題になります。
ここまでで分散は次の式で求めらると述べてきました。

実はここには隠れた大切な前提条件があるので詳しく解説していきましょう。
まず例題の設定を再度、思い出しましょう。
製作所の工程で生産された部品の寸法の狙い値が5.00だったとします。
最初に生産された5個の部品の寸法はたまたま4.68, 4.82, 4.88, 5.02, 5.10でした(狙い値は5.00)。5個の平均は4.90です。

しかしながら量産において5個しか生産しない部品は滅多にありません(ただの試作になってしまう)、普通に考えると10個、100個、1000個と生産は続きます。場合によっては10000個とか作るかも知れません。

この時に1000個、10000個と生産した全ての部品の寸法の平均が、例に挙げた5個の平均寸法4.90になるでしょうか?基本的に狙い値は5.00なので生産すればするほど狙い値の5.00に近づくのが普通です(これから大量生産を始めるので実際の全体生産の平均寸法はわからない)。

この時に最初の5個の部品の寸法の平均4.90と生産全体の平均になるであろう5.00に近い値とおよそ0.10に近い差が出てくるはずです。
そうすると最初に作った5個の部品の寸法だけで算出した分散(平均は5個の平均)と5個の部品の寸法と生産全体の平均を使って算出した分散の値は同じにはなりません。
ここで”値が異なって困ったな”ということになるので最初の5個のデータでなんとか生産全体の平均を使った分散が算出できないものか考えて行きましょう。
ここからは一般化するために変数を使って表していきます。
- 5個の部品の寸法のデータ、$x_1、x_2、x_3、x_4、x_5$でi番目の寸法は$x_i$
- 5個の部品の平均$\bar {x}$(バーエックス)
- 生産全体での平均μ(ミューと読みます、これから大量生産なので未知数)

まずは5個の部品の平均$\bar {x}$を使ってばらつきの2乗を求めます(第1章と同じ)。
このままだと5個の平均$\bar {x}$を使ったばらつきの計算になってしまうので、生産全体の平均μを使って補正します。5個の平均と生産全体の平均の差を補正するので以下のように補正します。

今回はデータが5個ほどあるので全てを書き出すと以下のようになります。

わかりにくいのでまとめます。

上の式は生産全体平均μを使ったばらつきの2乗と同じことになるので次のよう書けます(これのために補正した)。

ここで両辺を5で割ると

これで生涯生産の平均μと5個の平均xを使った2種類の分散の形が見えます。
これなら$(\bar {x}-μ)^2$を上手く処理できればなんとかなりそうな気がします。ただしμは未知数なのでこのままではどうしようもありません。
ここで期待値という概念を使ってなんとか処理していきます(分散は期待値とほぼ同義なので問題なし)。
※期待値については記事内の最終章に概要を記載しますので気になる人は先に確認してから戻って来てください。
期待値解説へのページ内リンク
ここから先は期待値なので各式をE[]で閉じます(期待値の英語のEXPECTED VALUEのE)。
ここで$E[(\bar {x}-μ)^2]$を$x_1、x_2、x_3、x_4、x_5$を使って書き直します。
ここで$(x_i-μ)を表記が面倒なのでe_i$と置きます。$e_i$は$x_i$からμ(確率とは関係ない未知数ですが必ず規定値になる)を値を引いただけなので$e_i$は$x_i$の期待値と同義で使えます。
これを展開すると

期待値αe1e2、βe1e3・・・・はお互いの存在を打ち消しあうので0になります。
※期待値の直交性、詳しくは記事末尾の期待値の解説へどうぞ
期待値解説へのページ内リンク
これを元に戻すと

これでなんとなく扱えそうな気がしてくるので元の式に戻しましょう(書くのが面倒なのと読み間違いが発生するので期待値を示すE[]は省略)。

通分すると

右辺の第2項を左辺に異動します。



見えて来たでしょうか?左辺の分母は5で右辺の分母は5-1になります。
つまり生産全体の平均を使った分散は、5個の平均のばらつきの2乗の和から最初の生産数5から1を引いた数で割ると求められることがわかります。
これを数をnとして一般化すると下のように書けます。

これがn-1で割ることの意味になります。
ここからは実際に
- 最初の5個の寸法と平均$\bar {x}$(4.90)を使った分散$S^2(\bar {x}=4.90)$
- 最初の5個の寸法と生産全体での平均μ(狙い値5.00になったとする)を使った分散$S^2(μ=5.00)$
- 最初の5個の寸法と平均$\bar {x}$(4.90)をn-1=4で割った分散$S^2(n-1=4)$
の3つを計算してみます。
- 分散$S^2(\bar {x=4.90})$=0.022
- 分散$S^2(μ=5.00)$=0.032
- 分散$S^2(n-1=4)$=0.027
ここで興味深いのが平均4.90と生産平均5.00を使って計算した分散は丁度0.01ほど違います($0.1^2$の違い)。
一方でn-1(5-1=4)を使った分散は0.027で0.032まで届きません(μは5.00に近いはずなので近い数字になるはず)。
この差は生産全体の平均μを最初の5個の寸法の値から推測する期待値計算で予測していることによって生じます(本来は生産全体平均の値はわからない)。
ここが統計の妙でn-1=4を使って算出した分散(0.027)は、正確な生産全体の分散(0.032)にはならないが、n=5で算出した分散(0.022)よりまともな値に近づくからn-1を基本的に使おうという理屈になります(基本的に生産全体の分散はわからないことがほとんど)。
分母の分散のnとn-1の違いの概念
ここまではかなり具体的な例、数字を使って説明してきたのでここからは概念を数学的な説明をして一般化していきましょう。
例題の設定をつかって数学用語を解説します。
製作所で生産された最初の5個の部品の寸法は、数学的に言い換えると生産全体全体の寸法はわからない中で適当に取り出した5個の標本ということになります(n数5の標本)。
その5個の部品の寸法の平均$\bar {x}=4.90$は標本平均と呼ばれます。

一方でよくわからない生産全体での寸法たちは母集団と呼ばれ、その平均μ(5.00に近づく寸法、実際には未知数でよくわからない)は母平均と呼ばれます(生産全数はNとしましょう)。

これらのデータから求められた分散は以下のように呼ばれます。
- $\frac{1}{n}\sum_{i=1}^{n} (x_i – \bar{x})^2$は標本分散
- $\frac{1}{N}\sum_{i=1}^{N} (x_i – μ)^2$は母分散(実際は求められないことがほとんど)
ここでの重要な条件が母分散は求められないから標本のデータを使って推測することになります。

その推測する式は上の章の途中で導出した以下の式になります(左辺は母集団そのものではないことに注意、標本のデータと母集団の母平均μを使った分散)。

上の式の右辺の右端$(\bar {x}-μ)^2)$がズレ量そのものなります。
そのズレ量は期待値を取ると以下のように表せることを上の章で導出しました(期待値による推計、分散と異なって分母が$n^2$が特徴)。

これらのことから以下の式が成り立ちます(もしよかったら上の章を参考に算出してみて下さい)。

ここで導出された を不偏分散と呼びます。この式の面白いところは母集団の分散は求められないから標本の数字を使って数学的な推論で求めた母集団の分散になります。
整理すると分散は全部で3種類
- $\frac{1}{n}\sum_{i=1}^{n} (x_i – \bar{x})^2$は標本分散
- $\frac{1}{n-1}\sum_{i=1}^{n} (x_i -μ)^2$は不偏分散(標本からの母分散の推測)
- $\frac{1}{N}\sum_{i=1}^{N} (x_i-μ)^2$は母分散(実際は求められないことがほとんど)
関係性としては求めることが不可能な母分散を数学的に推測したのが不偏分散ということです。
実際に計算した場合の関係性は標本分散<不偏分散<母分散(基本的に求められない)で不偏分散は母分散に近い値を推測して算出できることになってます。

標本分散よりばらつきが大きめになるから実態として不偏分散は、標本分散そのままより安心して使えることが多いです。
nとn-1の差と影響度(数学と工学の違いのポイント)
ここでは実際に標本分散(nで割る)と不偏分散(n-1で割る)の数値の違いを具体的に見て行きましょう(工学的に非常に重要なことです)。
不偏分散から標本分散を割って100を掛けて不偏分散の増加率を見て行きます。

この式でnを2から100くらいまで増加率を計算した表は以下のようになります(n=1は分散の計算方法では存在しない)。

サンプル数が25を超えたあたりから急激に差が縮んでいることがわかると思います(nが25を越えると差は5%未満まで下がる)。
折角なので増加率をグラフにしてみます。

グラフを見てもわかるように30個以降は不偏分散と標本分散の差はほとんど変わりません。
このことから冒頭で述べたように30個のデータがあれば不偏分散(n-1)と標本分散(n)の差はほとんどない(3%レベル)なので標本分散(n)でも実用上は問題ないと言えるわけです(やっと伏線を回収できた)。
さらに面白いことに標本分散が不偏分散に近づくと標本の分布が限りなく母集団の正規分布に近づいたとも言えます。
この統計学の性質を利用して工業製品の1ロットの数は30個前後になることがほとんどです(実際は25~30個)。
1ロットの中から適当に2,3個ほど部品を抜き取って検査をすればそのロット全体の全体の品質が保証できるわけです(抜き取り検査を30個前後でやる理由もこれ)。

また定期的にロット全体(30個レベル)の部品の寸法を使ってグラフを作成して分布をチェックすればこれから生産する部品全体の分布もわかってしまう優れた理論です(いずれも分布が正規分布に従うことが前提条件)。
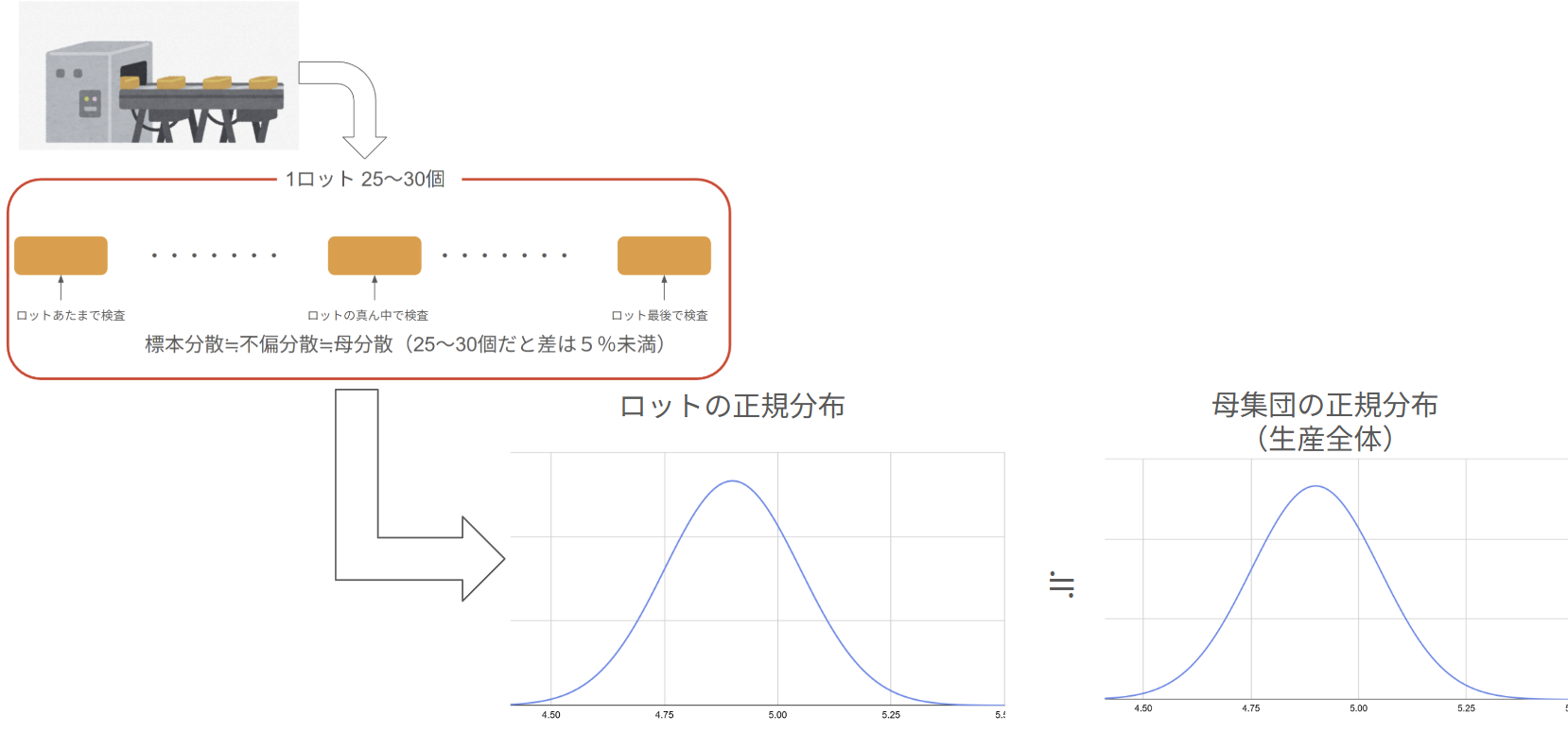
逆に検査もしないで1ロットで30個を大幅に超える数の100,200個とかを一気に作ってしまうと抜き取った検査でNG品が出た場合にとんでもない数の不良品を作ってしまったことになるので1ロット30個前後に収めます(工程のチェックが遅れて大惨事になる)。
※検査もしないで一気に100個、1000個も作ってしまう製品は品質が怪しいと判断できる理由です。

この理屈は普段の生活に生かすこともできます。
例えば何かの製品を買って不良品を引いてしまったときにお店に交換をしてもらう場合は同ロット品は避けてより新しい生産品を要求しましょう(製品に記載されているロットナンバーでわかる、以後の生産工程は修正されてる可能性が高い)。
また理工系の学生さんならば試験で分散を求める問題が出て分散を求める際にn、n-1で迷ったら、nで計算した結果に”n数が多いから問題ない”と追加で書いておけば〇にはなりませんが×にならず△で点は貰えるはずです(保証はできませんがnかn-1でのギャンブルよりはマシなはずです、数学科とか理学系では無理かも)。
まとめ
ここで分散でn、n-1のどちらで割るのかをまとめて行きましょう。
・nを使って求めた分散は標本分散:標本分散は標本内だけの値

・n-1を使って求めた分散は不偏分散:不偏分散は標本のデータから母分散を推計した値

・標本分散<不偏分散となり基本的に不偏分散は母分散に近くなる
(もし迷ったら不偏分散を見とけばバラツキを多く見積もれるので安心できる)
・n数が25を越えると不偏分散と標本分散の差は5%未満、工業ではn数が25以上が多いので標本分散を使っても問題ないことが多い

・試験で迷ったら標本分散を求めて、n数が多いから問題がないと書けば点が貰える可能性が高い
以上がまとめになります。
私が経験した機械工業の世界ではn数が25を超えることがほとんどで標本分散を求めていたことがほとんです。標本分散で問題ないとは言え標本分散(nで割る)と不偏分散(n-1で割る)の意味を分からないで使うよりは意味がわかって使い分けた方が安全だと思いますので是非、参考にしてください。
以上、分散はn、n-1のどっちで割るか?の解説でした。
期待値の簡単な説明
記事末の付録として期待値について簡単に概念を解説します(高校数学を思い出してみましょう)。
期待値とは1回の試行で”平均的にどれくらいの値が期待されるか”を示す数値で値x×発生確率P(x)で算出できます。
なんのこっちゃよくわからないのでサイコロの目と発生確率を使って考えて行きましょう。
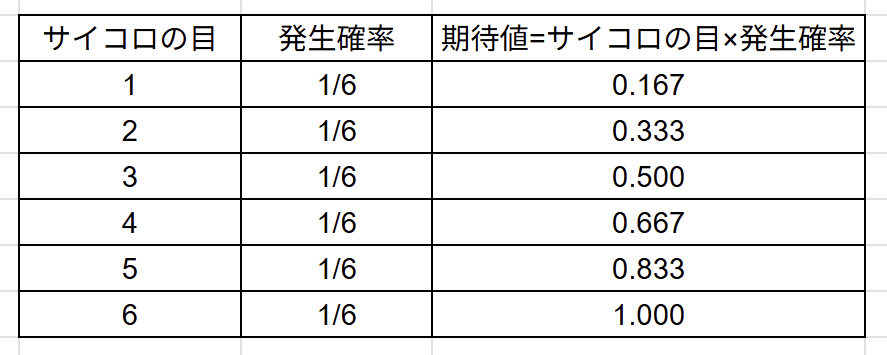
上の表のサイコロの目と発生確率を掛けて足し合わせます。
これが期待値です。
意味としてはサイコロを振った時にサイコロの出る目はよくわからないが期待値の3.5を見込んでおけばとんでもない外し方はしないだろうという意味になります(最初の1と最大の6から均等に離れた3.5を落としどころにする)。
ようするにどんな値になるかよくわからない事象を確率を使っていい感じの落としどころを求めることになります。
上の章ではこの期待値を使ってよくわからない$E[(\bar {x}-μ)^2]$を処理しました。
式を展開すると(流石に2度目で面倒なので途中は省略します)
ここで期待値を取ると$x_i$は$x_i×発生確率P(x_i)=X_i$とします(寸法も発生確率もよくわからないから変数のまま)。生産全体の平均は未知数ですが確率によって変動する値ではないのでそのままμです。
期待値に変換して展開すると以下の式になります。
※α、β・・・は展開して出てくる整数。$(x+y)^2$の展開で出てくる2xyの2みたいなモノ。
ここで$(X_i-μ)$の期待値を考えて行きます。
ここで一度、サイコロに戻って考えましょう。
設定としてはサイコロを振って出た目から3.5を引いた値を考えます(期待値を平均と見做す)。

表を見るとわかるとおり-の成分と+の成分が等しいのでお互いを消しあって0になります。
設定に戻るすと$(X_i-μ)$も同じように0に収束して行きます(究極的には期待値は生産全体の平均に限りなく同じになるはずだからです)。
ただし$(X_i-μ)^2$は違った考え方が適用されます。
再びサイコロに戻って考えます。設定を変えてサイコロを振って出た目から3.5を引いた値の2乗を見て行きましょう。

どうでしょうか?2乗にすると-が二乗で消えて全てのサイコロの目で+になるので値は積まれて存在することになります。不思議なことに二乗すると値が存在することになります。
これは非常に重要な事で1章で解説したばらつきとばらつきの2乗の関係性と同じになり各ばらつきを二乗したことによって実際のばらつき量を正確に抽出していることになります(実は分散を求めているのと同義)。
よって$(X_i-μ)^2$はそのまま存在できることになります(二乗の項だけが積みあがる)。
この性質を使うと元の式は次のように書き直せます。
これが期待値の妙で以下のことが成り立ちます。
これによってわけのわからん$E[(\bar {x}-μ)^2]$を扱える形に推計したということです。
第2章の期待値を使った計算(ページ内リンク)
以上、期待値の概念の説明でした。




コメント