執筆時点(2021年初頭)でガスガンのCO2マガジンの安全な取り扱い方が少し話題になってます。
昨今の環境問題への取り組みを鑑みますとこれからCO2ガスガンユーザーが増えていくのは容易に想像できます。
折角の機会なのでエンジニア視点で強度計算をしてみます。
なお本内容はCO2ガスガンの賛否や特定の企業、団体や仕組みについて咎めることを目的としていません。
仕組みと作動環境
まずは今回は、密閉型と言われているマガジンを計算してみます。
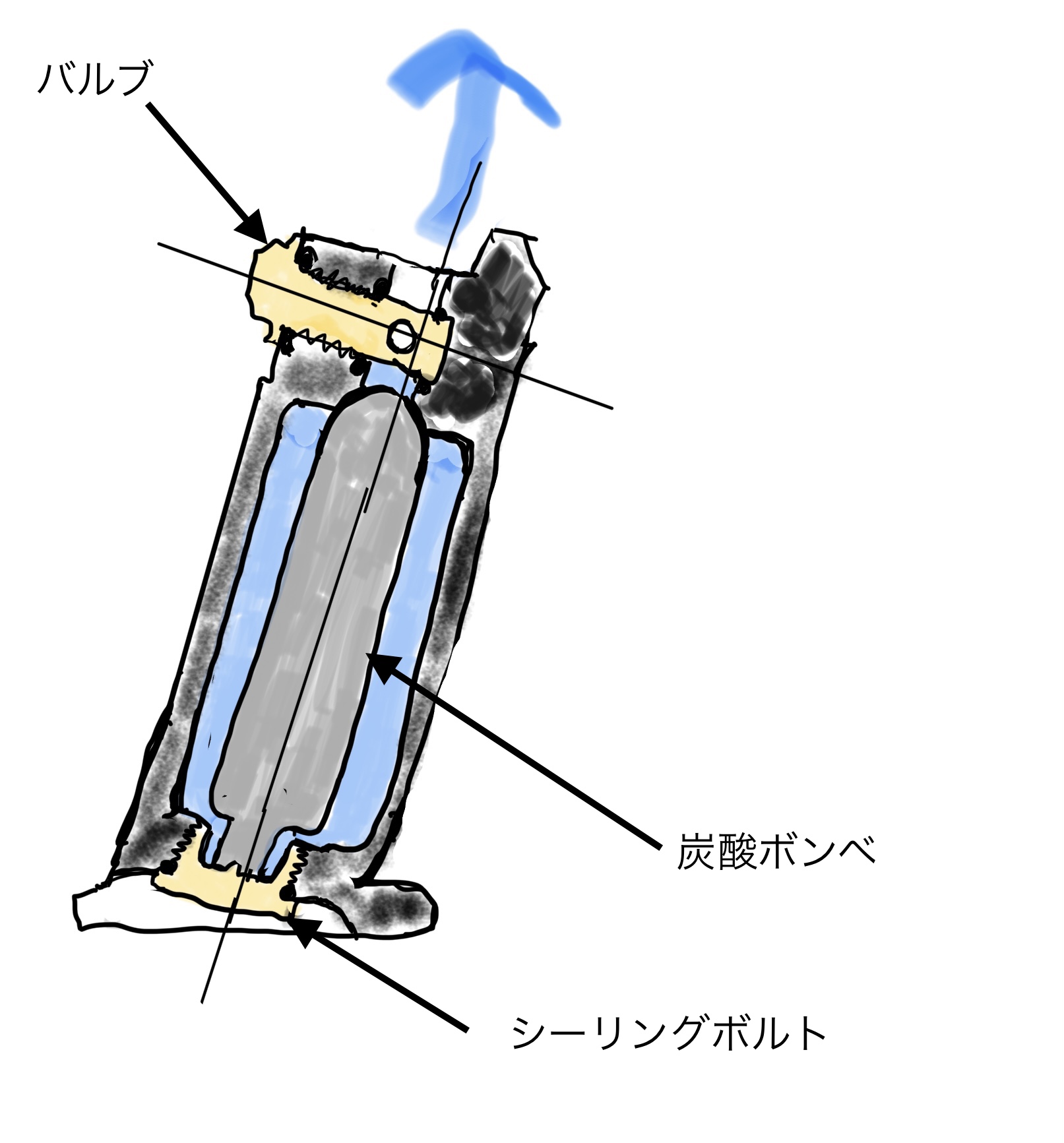
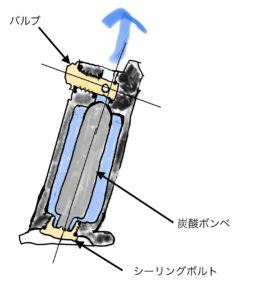
強度に関連する部品は以下のようにします。
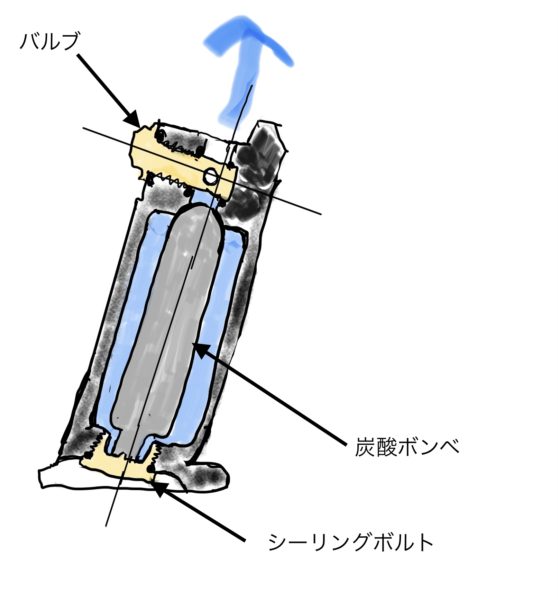
マガジン本体とバルブ、炭酸ボンベ、シーリングボルト(又は、キャップボルト)と部品を名付けます。
次に使われ勝手をフローチャート式で考えます。
炭酸ボンベ取り付け時

CO2マガジンが使用されるとき(BB弾発射時)
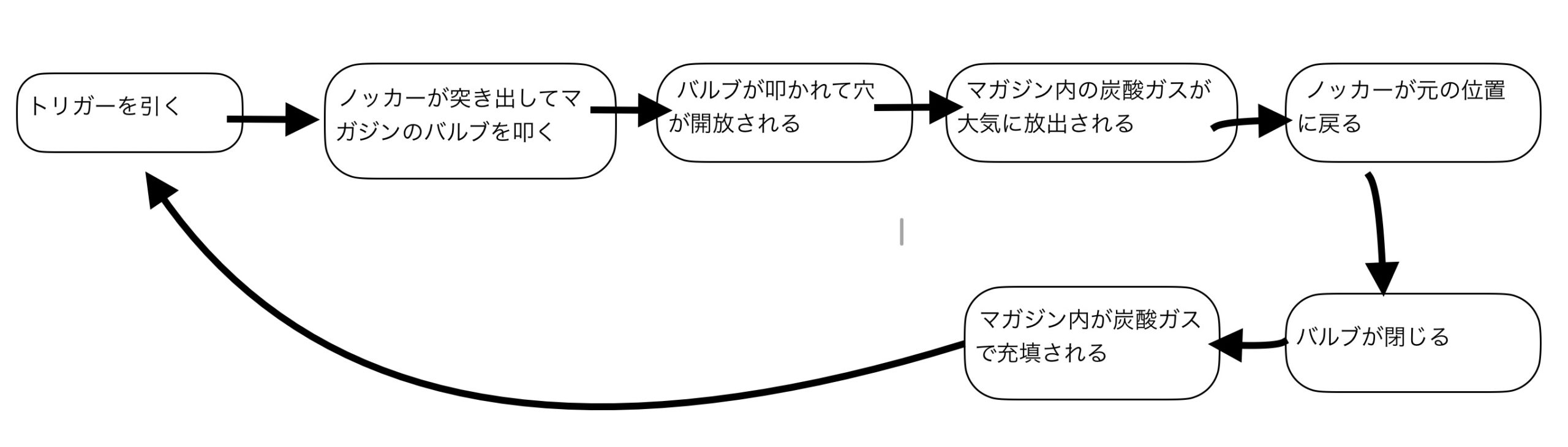
炭酸ボンベを外すとき

ざっとマガジンと炭酸ガスボンベの作動環境(ライフサイクル)はこんな感じでしょう。
弱冠、誘導尋問くさいところがありますが気にしないようにしましょう。
次にマガジン廻りの寸法を調べましょう。
マガジン廻り寸法の調査
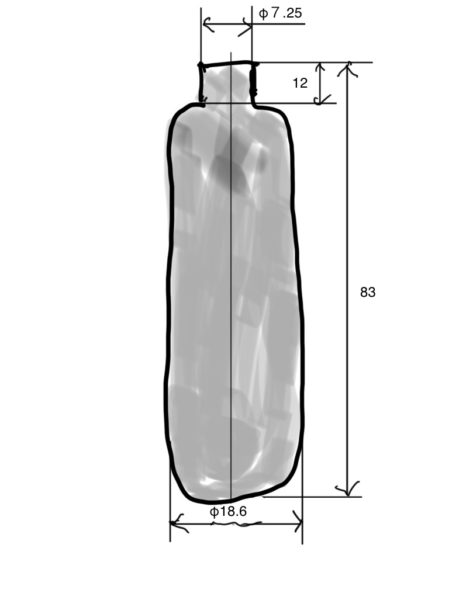
まずは規格品である炭酸ボンベの寸法の確認。某国内メーカーの炭酸ボンベを測定(ほとんど他と同じでしょう)します。
単位は全てmmです。
次にマガジンを測定しますが機種は、某国内最大手メーカーのグロック 17のマガジンにします。
理由はデフォルメされているとは言え世の中の多くを占める9mm、ダブルカラムタイプのマガジンの代表みたいなものなので同口径、ダブルカラムならば計算に影響を与えるような寸法差はないと予想します。(45口径や特殊弾は別ですが)
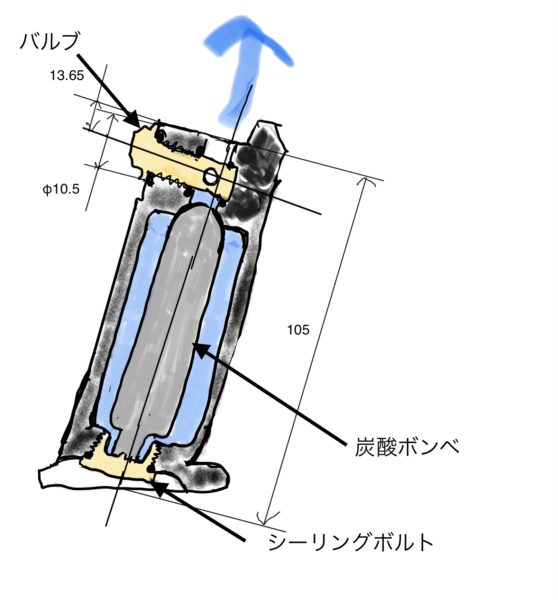
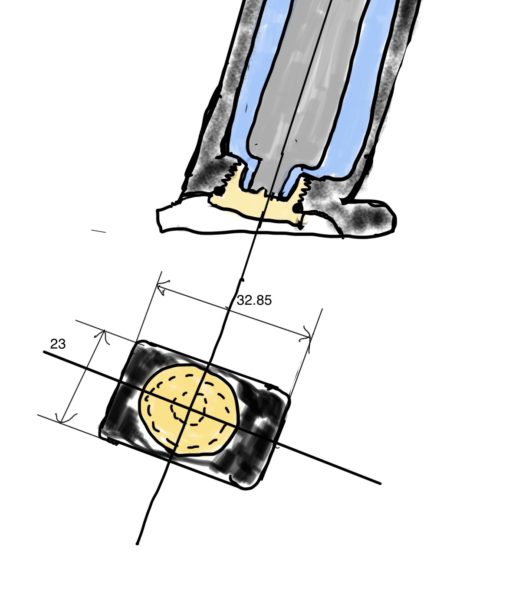
ここで架空のCO2マガジンを考えているのでシーリングボルトの寸法が不明ですが、調べた寸法からシーリングボルトが取り得る寸法の範囲がわかります。
まず取り得るシーリングボルトの最小径は使われ勝手のフローチャートより炭酸ボンベの取り外し可能にしなければならないので炭酸ボンベの外径18.6以上にします。
またギリギリの寸法だと炭酸ボンベの取り外しに支障が出ますので製造時の公差を半径で0.5、使い勝手で1のクリアランスとしましょう。
そうすると
φ21.6<シーリングボルト径
次にシーリングボルトが取れる最大径を考えます。
マガジンの幅が23なので当然、これよりは大きくできません。
シーリングボルト径<φ23
ボルトは規格で取り得るサイズが決まってくるのでボルトサイズはM22以外は選択できません。(実はM22と設定する場合、すでにめねじの強度的に成り立たなそう。)
ガスをシールするのでネジピッチは細目でJISでは、1.0なのでM22x1.0(下穴径を考えるとボンベがキツそう)。
次にシーリングボルトの長さを考えます。
シーリングボルト長さは割と自由にサイズが取れそうなのでこれは変数Lのままにして強度計算をしてみましょう。
シーリングボルト廻りのレイアウトのイメージ
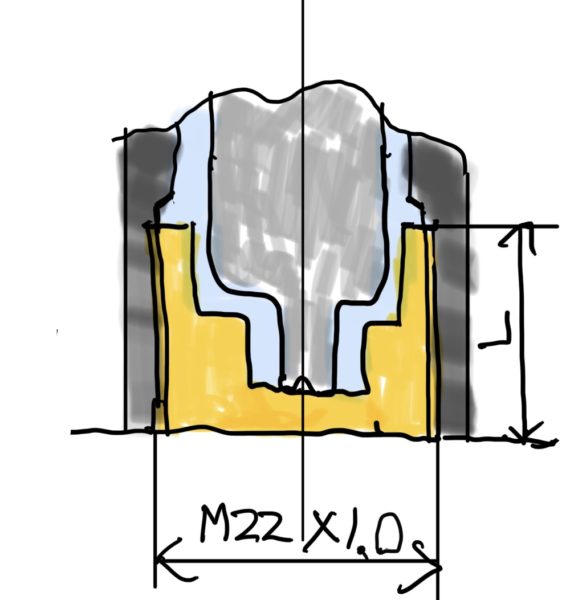
同様にバルブの取り得るサイズも自ずと決まってきます。
今回は、見た感じ着目点、私の経験上でシーリングボルトとマガジンの肉厚が気になるのでそこに注目します。
CO2マガジンに発生する力を調べる
作動ガスは炭酸ガスなのでサクッとネットで物性値を調べると(飽和蒸気圧曲線を見れば良い)
・温度6.3℃で4.0MPa
・温度10.9℃で4.5MPa
・温度15.1℃で5.0MPa
・温度19℃で5.5MPa
・温度22.9℃で6.0MPa
・温度26.1℃で6.5MPa
・温度31.1℃で臨界点7.38MPa
使用される環境としてはこのくらいで良いでしょう。結構ヤバい圧力です。
大気圧は、約100kPaなので40〜70倍もあります。
わかりやすくするために19℃で5.5MPaを中心に計算します。(多変量解析とか使えば飽和蒸気圧曲線の方程式をそのまま使える。モードフロンティアとか)
今回は、密閉型の計算ですので容器内は一様に5.5MPaの圧力がかかっているとして計算するとシーリングボルトにかかる力は圧力x面積なのでネジの有効径から面積を求めます。
M22x1.5のネジ有効径は規格よりφ21.0、面積は346.3($ mm^2 $)
よってシーリングボルトにかかる力は、$ 5.5×10^6×346.3×10^{-6}=1904(N) $
1.9kNになります。
うん、このくらいならネジは、大丈夫なのがわかります。(M6x0.8で10kNくらいまでいけます)
では心配事の残りはマガジンの肉厚です。
マガジン内の圧力はパスカルの原理より一定圧になるので19℃の5.5MPaと考えます。
また使い勝手チャートから弾の発射時にガスが解放されるのでマガジン内は減圧されます。
よって繰り返し荷重を受けるので疲労強度の観点も考える必要がありそうです。
しかし解放時の減圧度合いは分かりませんので大気圧、元の半分、元の2/3で考えてみます。
・大気圧まで下がる場合 イニシャル5.5MPa 平均圧力2.75MPa 振幅圧力 2.75MPa
・元の半分まで下がる場合 イニシャル5.5MPa 平均圧力4.13MPa 振幅圧力 1.38MPa
・元の2/3まで下がる場合 イニシャル5.5Mpa 平均圧力4.59MPa 振幅圧力 0.92MPa
と考えます。
次にマガジン内の発生応力を考えて行きましょう。
マガジン内の発生応力
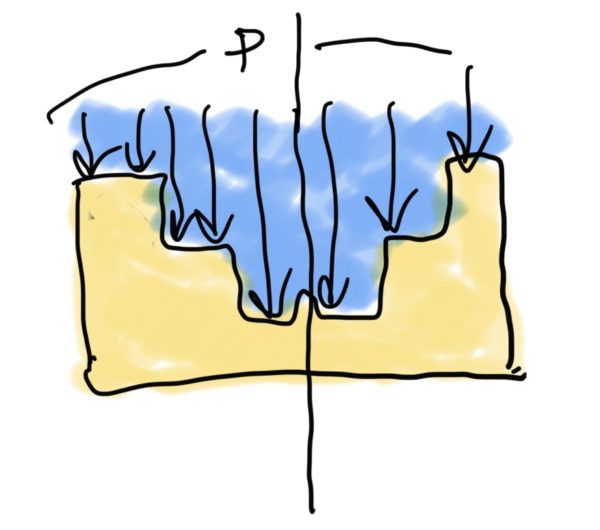
ではマガジン内に発生する応力を求めるのですがCAEなどがないので形状を単純化して考えます。
薄肉円筒容器として考えていきます。
円筒圧力容器の応力計算の詳細は、こちら→初心者でもわかる材料力学26 薄肉圧力容器の応力(円筒圧力容器、球型圧力容器、圧力容器全般)
まずマガジンを単純な円筒と見立てて肉厚をtとします。
また応力発生部分を上下蓋の円周部と円筒部位に分けて考えます。
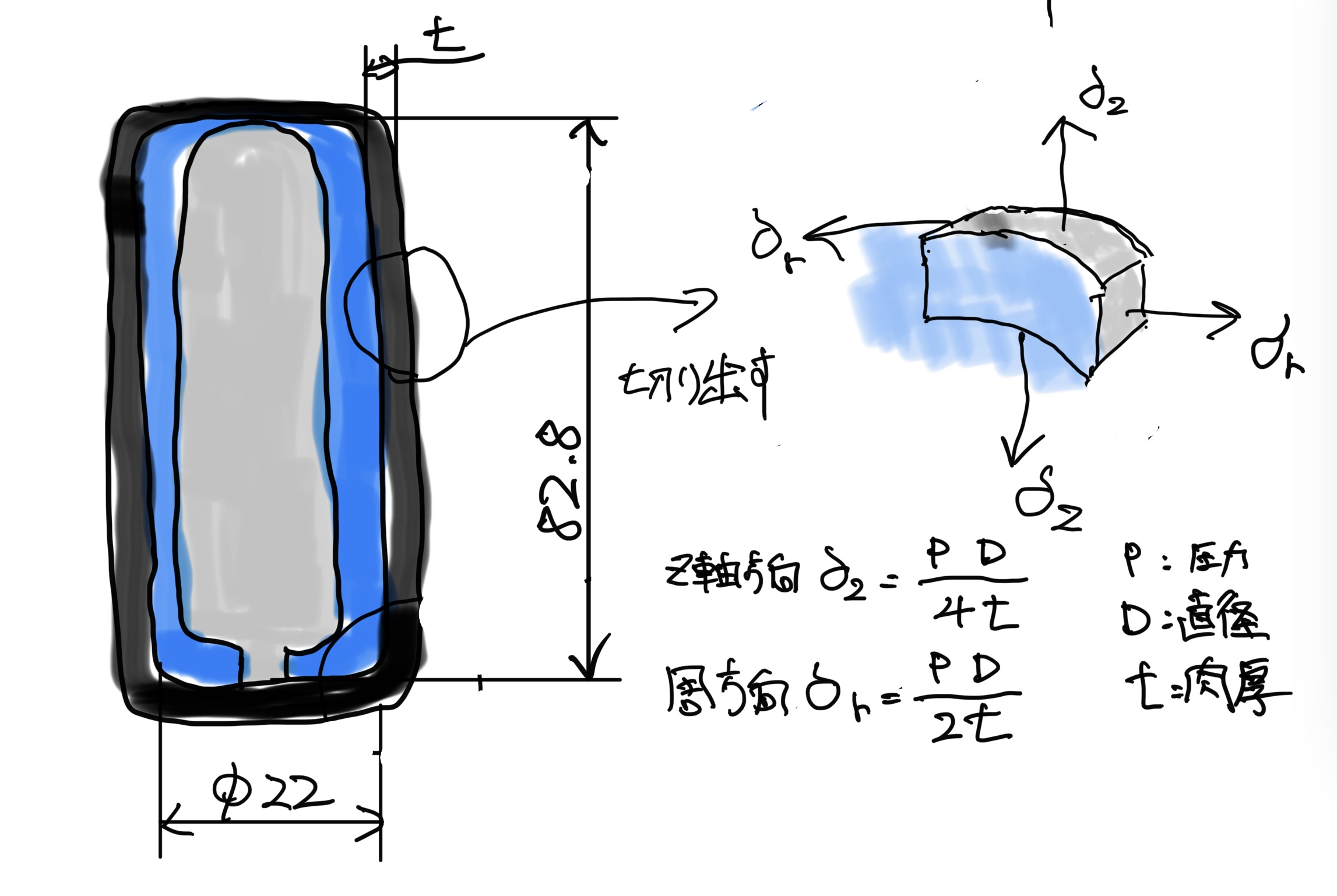
公式があるのでサクッと求めると圧力をP(MPa)、肉厚をtとすると
底の部分の応力(軸方向) $ σz=\frac{P・22・10^{-6}}{4・t・10^{-6}}=\frac{5.5・P}{t} (MPa) $
周方向の応力 $ σr=\frac{P・22・10^{-6}}{2・t・10{^-6}}=\frac{11・P}{t} (MPa) $
となりPの取る値の範囲とtの取り得る範囲を考えます。
Pは物性値から4〜7.38(MPa)で肉厚tについて考えるとマガジンの幅が23でネジがM22x1.0で規格より下穴がφ21で図にしてみると
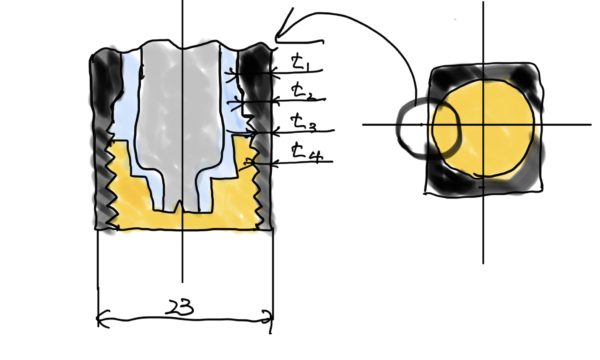
一番、肉厚が薄くなるのはめねじの谷の径と外側t2で計算すると
めねじの谷の直径は規格よりφ22でマガジン幅は23なので0.5(もう怖い)
同様にt4は、めねじの山の直径がφ20.917なのでおよそ1
t2はめねじの下穴の直径がφ21なのでまあおよそ1
残ったt3はボンベに当たらなければ良いので極端に考えるとボンベ直径φ18.6から2.2
よってtの範囲は0.5<t<2.2となります。
条件が整いました。4<P<7.38 0.5<t<2.2で発生応力の表を作成します。
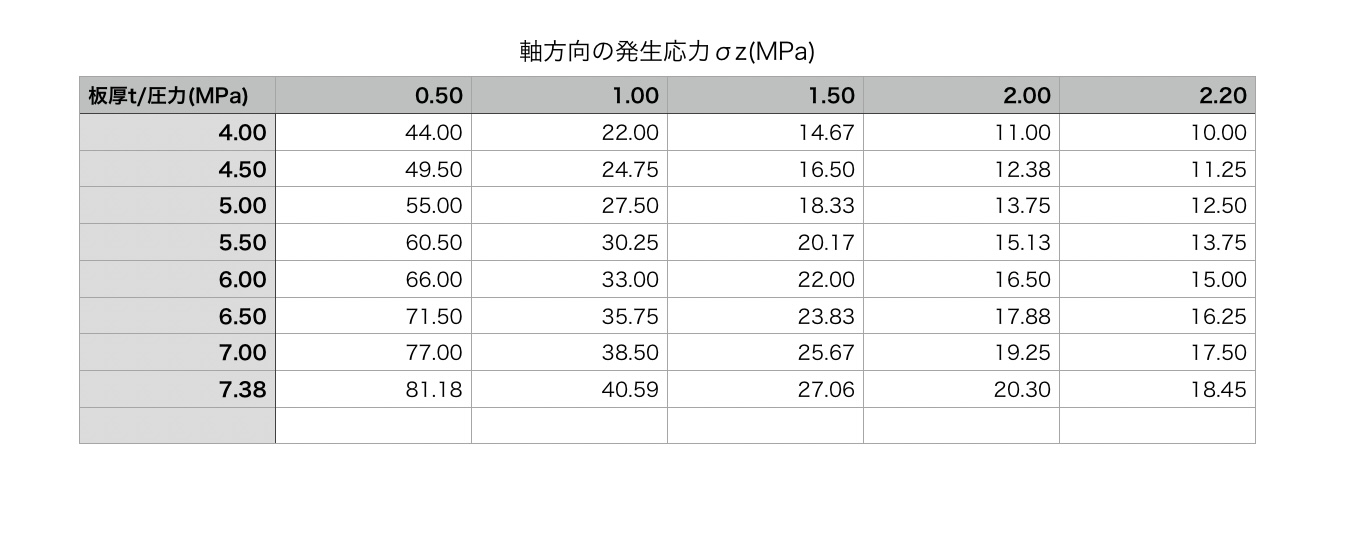
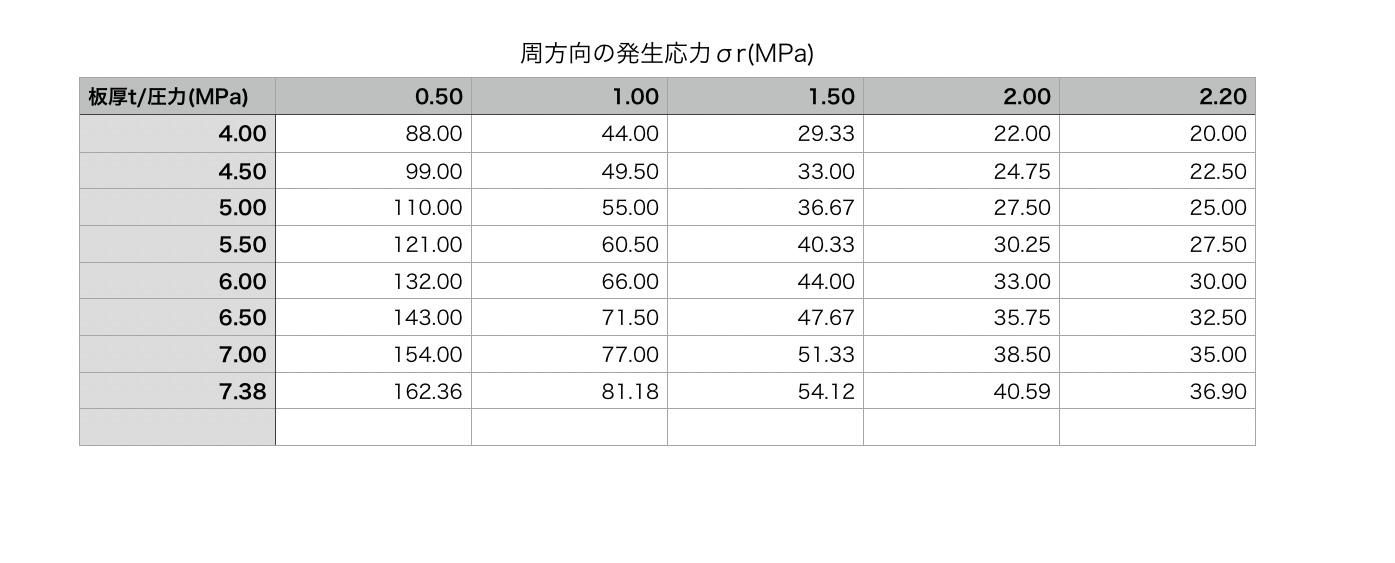
本当は3次元のグラフを書きたいのですが、私の今の環境では無理なので表だけにします。
これで発生応力がわかりました。次に材質の物性値を見ていきます。
マガジンの材質
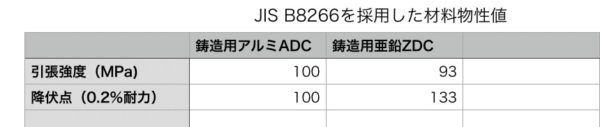
マガジンの材質はコスト、重量、量産性から考えると選択できるのは鋳造用のアルミか亜鉛でしょう。(鋳造用アルミはADC,亜鉛ZDCと表す)
常温での二つの物性値をみると(色々な材料があるが大体の平均で表を作成する)

私がよく使っているアルミだと鋳造品質やクリープ、脆性破壊を考えるとアルミの降伏点は、100MPa程度に考えたいのですが今回はジャンルが異なるホビーということで表の値を使います。
また圧力容器の設計にはJISで以下のように定められています。JISは長い文なので必要な所を抜粋すると
発生応力100MPa以内の場合,次の値のうちの小さいほう以下とする。
(今回、100MPaを超えている領域がありますがおまけしてこれを使います。本当は使っちゃダメですよ)
1) 常温における規定最小引張強さの$ \frac{1}{3} $
2)各温度における引張り強さの$ \frac{1}{3} $
3)常温における規定最小降伏点または0.2%耐力の$ \frac{1}{1.5} $
4)各温度における降伏点または0.2%耐力の$ \frac{1}{1.5} $または0.9
となっておりJIS B8266を採用するとなると材料の物性値は次のようになります。
亜鉛の降伏点が引張り強度より高いのが意味が分かりませんが、まあ私の感覚的に安全に使うなら“こんなもんかな“という気がして納得できる値です。
強度の判定
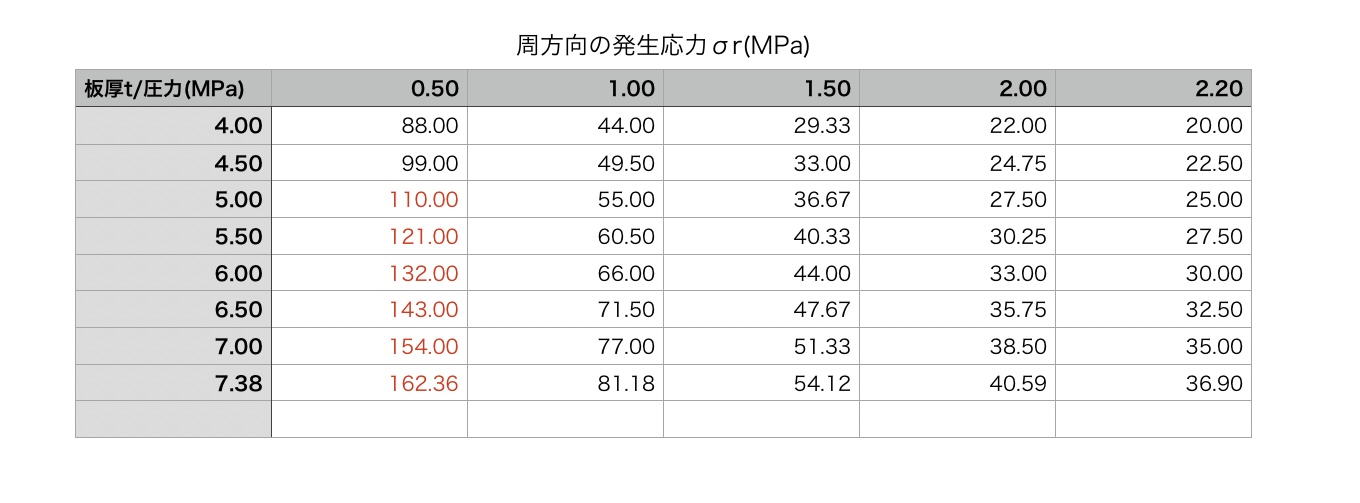
では発生応力と材質から強度の判定をします。
発生応力は、周方向の方が大きいので周方向応力σrで見ていきます。
また使われ勝手フローチャートから振幅応力が発生することから弾性域での利用が原則になるので降伏点(0.2%耐力)内で判定します。
まずはJIS B8266を考慮したアルミADCの場合は、(赤字の部分が破損領域)
次に亜鉛ZDCの場合は
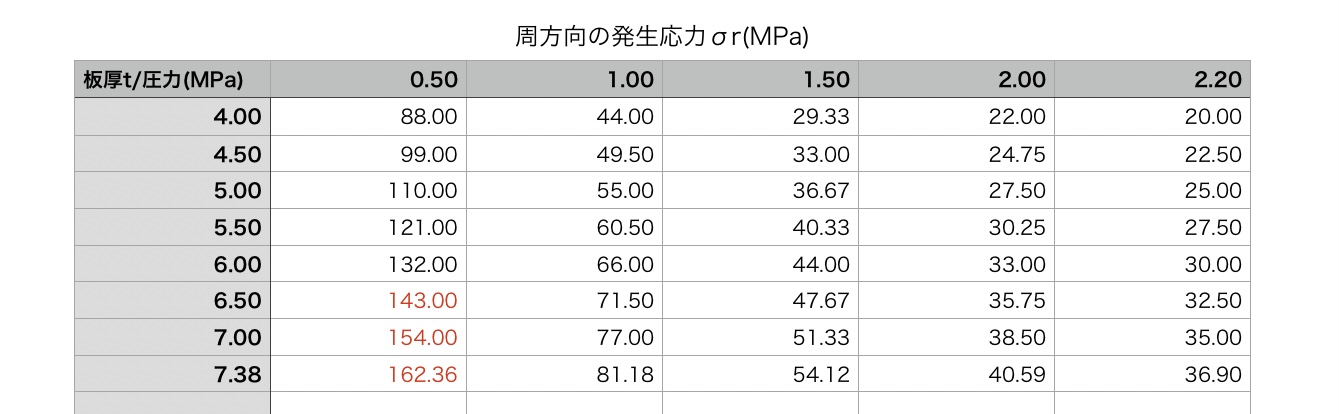
となりJIB 8266を採用するとなると仕様が成立するとは考えられなさそうです。
また単純に材料の強度と照らし合わせるとアルミの場合は圧力によっては成立しない領域が出てきます。
結論と考察
結論としては、
某国内最大手メーカのグロック 17サイズのマガジン幅23 、規格品の炭酸ボンベを使う密閉タイプ、シーリングボルトがM22x1.0、材質がアルミダイカスト材もしくは亜鉛ダイカスト材の場合に仕様は成立せず、破損する可能性が高い
となりました。
最小肉厚が0.5mmですが鋳造品質や加工ズレ等が発生し、さらに肉厚が減少すると引張り強度を超え、一発破壊が発生する可能性が高いです。
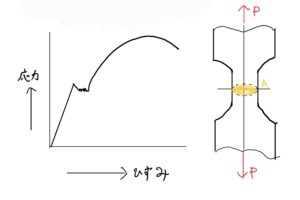
破壊のイメージとしては図のようになります。
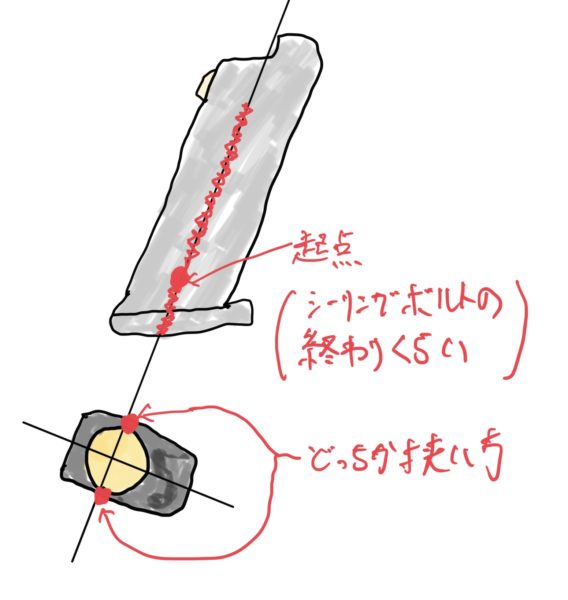
対策としては最小肉厚を鋳造品質、加工ズレなどのもろもろを考えると1.5、いや2くらい欲しいところでマガジンの幅を拡大した方が良さそうです。
もしくはガス圧を下げて使う、リリーフバルブを使うといったところでしょうか。
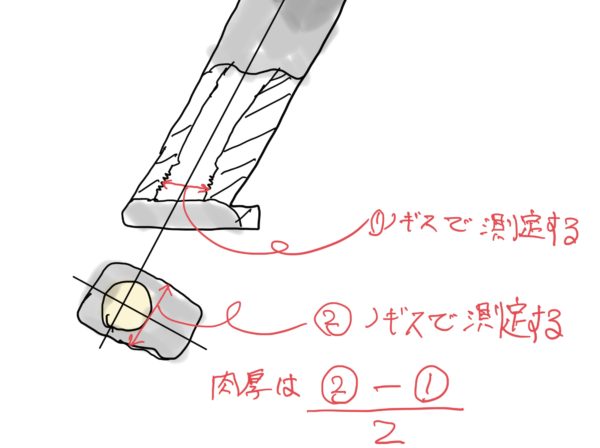
もし皆さんのお手元にこの強度計算で想定したサイズのCO2マガジンをお持ちでしたらシーリングボルトのネジの谷とマガジン幅を測定して肉厚が最低1mm以上あることを確認することを強くお勧めします。
もし1mm以下の肉厚ならば安全面を考えて勿体無いですが廃棄することを強く勧めます。
もし破損した場合に4MPa~7.38MPaという大きな圧力が解放されるので非常に危険です。
測り方は図を参考にしてください。
めねじの谷の直径がうまく測れない場合は計った値からググってネジの規格を見てネジサイズを特定してめねじの谷の径を調べましょう。
ネジの規格は絶対にすぐに見つかります。
また炭酸ガスが空になる前にシーリングボルトを外すのは絶対にやめましょう。
ガス圧がそのままでシーリングボルトのネジのかかり代が減って発生応力が高まるとシーリングボルトが高速で吹っ飛びます。
最悪、怪我をします。
楽しく安全に遊ぶためによく説明書を読み注意して取り扱いましょう。
また説明書に書いて思うのですが遊び終わったらなるべくガスを使いきってマガジンからボンベを取り外して保管しましょう。
高い応力が長い時間、発生し続けると少しずつ歪みが溜まって来て温度変化や少しの刺激で破損することがあります(クリープ現象)。
感想として検討前の私の予想では作動によるマガジン内のガス圧変動で疲労破壊しているのかと思っていましたが、それ以前のいきなり壊れる一発破壊を発生する可能性が非常に高く驚きました(設計的に有り得ない)。
皆さんも商品選びには気をつけましょう。


コメント