前回からの続きでとっても大切な物体の弾性と材料の基本的な特性を解説する。
今回の解説も機械設計において超重要なので頑張ってついて来て欲しい。
また初心者でもわかる材料力学を最初から順に学びたい人はこちらの索引からどうぞ→初心者でもわかる材料力学シリーズ
また決まり事が多いのだが前回の最後に述べたように暗記が大切なのではなく正しい検索能力が機械設計者には大切なので、どこに何が書いてあるのか是非、記憶しておいて欲しい。
弾性ってなんだ
まず材料力学でとっても大切な弾性の概念について説明しよう。
弾性とは簡単でバネと一緒で物体が延びたら元に戻ろうとする力が働き$ 定数=\frac{応力}{歪み} $の関係が成り立つ場合を弾性体という。
また、ここで定義された定数は、Eで表され弾性係数と呼ばれ、大切な物性値になる。
このような関係をフックの法則というが名前はどうでもいい。
堅苦しい言い方はここで終えて、具体的に図で解説する。
まず、ただのバネを想像して欲しい。

まあ、当たり前だがバネを引っ張れば元に戻ろうとするのでP=kxとなるのはわかると思う。
実は多くの物体にもこの関係が成り立つのだ。
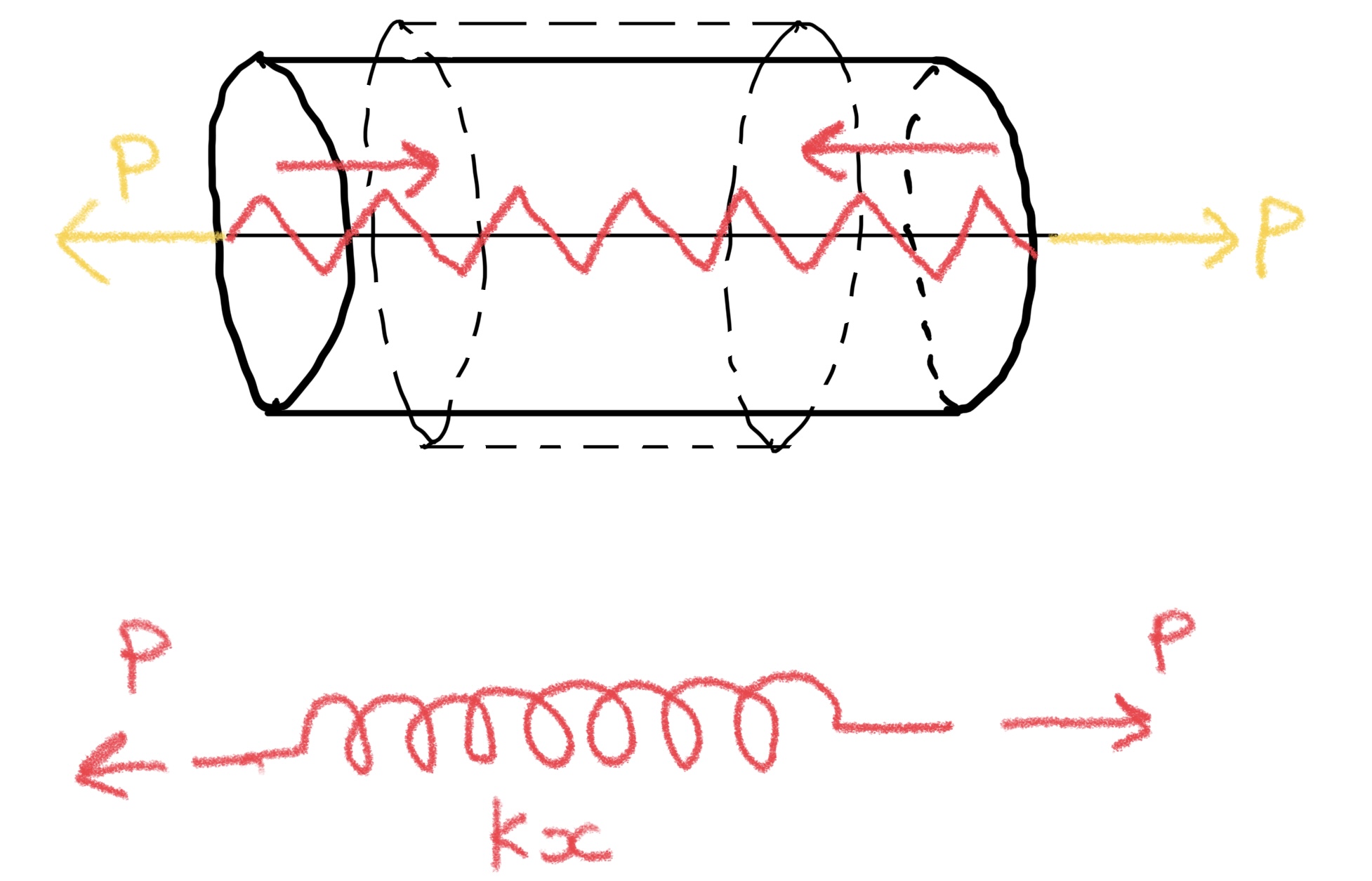
誤解を恐れずに例えると物体もバネと一緒である。
ただしここからがポイントで
バネは伸びた量xに対して戻る力kx(ばね定数×距離)が決まるのと同様に物体は歪んだ量εに対して戻る応力Eε(弾性係数×歪み)が成立する
$ σ(応力)=E(弾性係数)×ε(歪み) $
弾性係数Eとはバネのバネ定数Kはとても似ている。E(弾性係数)の単位はパスカルPa
ここで出てきた弾性係数Eは単位がPaで、定数になり材料によって決まっている。
ある程度機械設計をやってると鋼は210GPa、ジェラルミンは70GPaくらいと覚えてしまう。
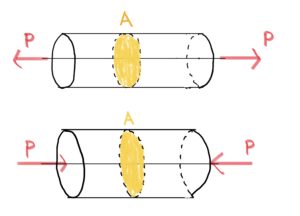
同じように剪断力に対してもこの法則は成り立つ。
前回の剪断の例を思い出してほしい。
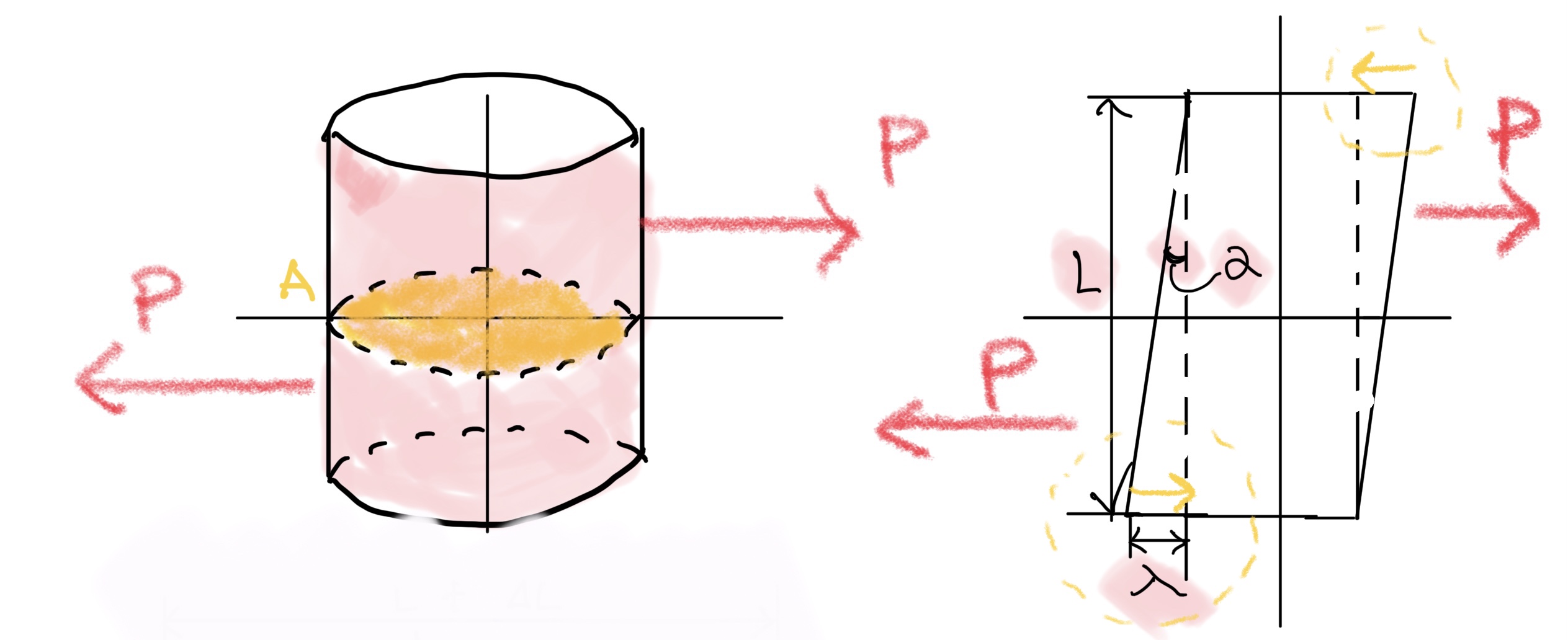
図の右側の黄色い矢印に着目してもらいたい。
引張りと同様に元の形に戻ろうとするので
$ τ(剪断応力)=G(剪断弾性係数)×λ(歪み) $
G(剪断弾性係数)の単位はパスカル(Pa)
で弾性係数Eと同じように剪断弾性係数Gは単位がパスカルPaで、材料ごとに値は決まっている。
これまでの説明で物体もバネと同じで、元に戻ろうとする応力が発生しその関係を弾性と述べてきた。
しかし物体の歪み量がどんどん増加していくと、この法則が成り立たなくなる。
この関係を見るのに応力歪み線図というグラフを利用する。
応力-歪み線図
応力-歪み線図は何もんだ?と思うかもしれないが丁寧に説明していく。
引張り試験
まずJISで形や寸法が決まっているくびれた棒を機械で引っ張るのだ。
まあ、これを標準試験片というのだが名前はどうでもいい。
ポイントはカタチが決まっているということなのだ。(詳細が知りたければ各自でJISを調べて見て欲しい)
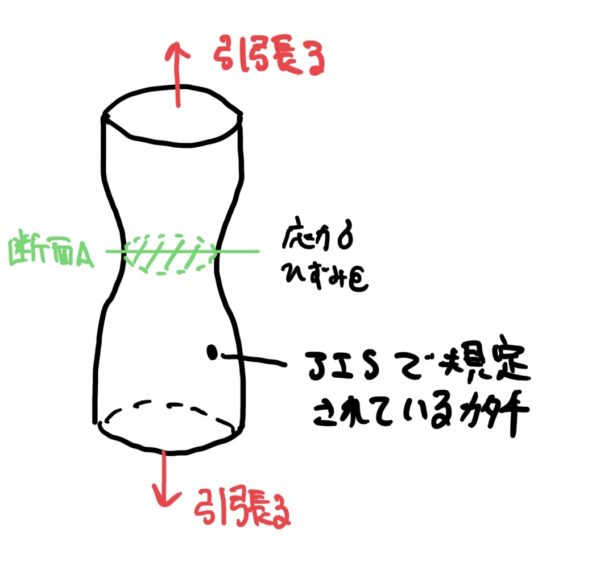
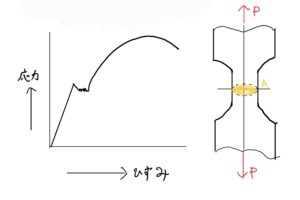
この試験で物体を引っ張るときに断面Aに発生する応力と歪みを計測して横軸に歪み、縦軸に応力としてグラフを作成する。
これを応力-歪み線図という。これは、名前も大切。
基本的な物体の特性は以下の図のようになる。
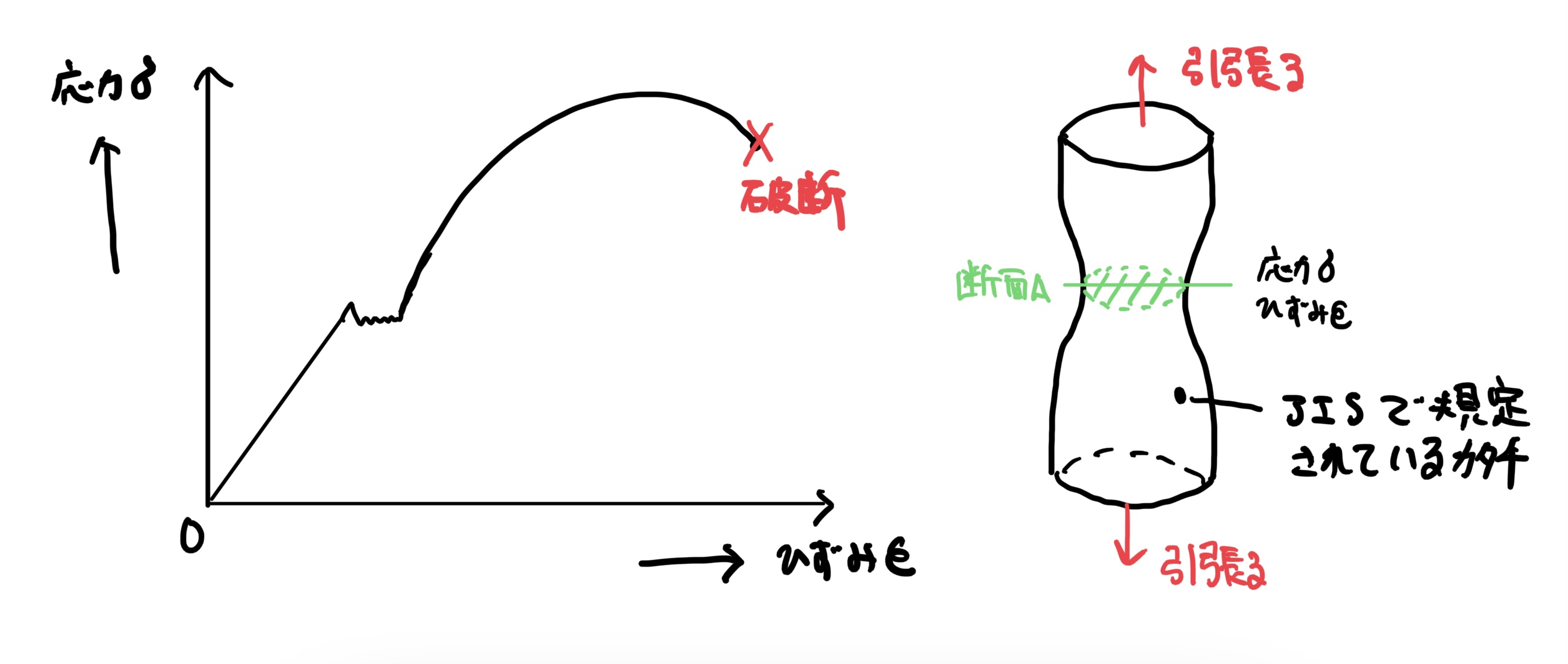
これはかなり重要なので是非、覚えといてくれ。
応力-歪み線図
ここからは具体的に応力-歪み線図の見方を説明していく。
まずは、座標軸原点の0からの直線部分について説明しよう。
弾性域
いきなりポイントで申し訳ないが重要なことを述べる。
座標軸原点oからの直線部は弾性域と呼ばれれ、フックの法則が成立する範囲のことである
お気づきの方もいると思うが、そう今回、説明した物体がバネみたいな特性を持つ領域のことである。
ここで凄く重要なのが引っ張ったら完全に元に戻るということなのだ。
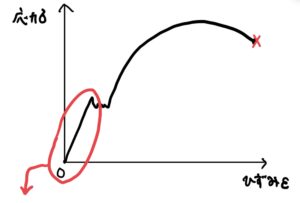
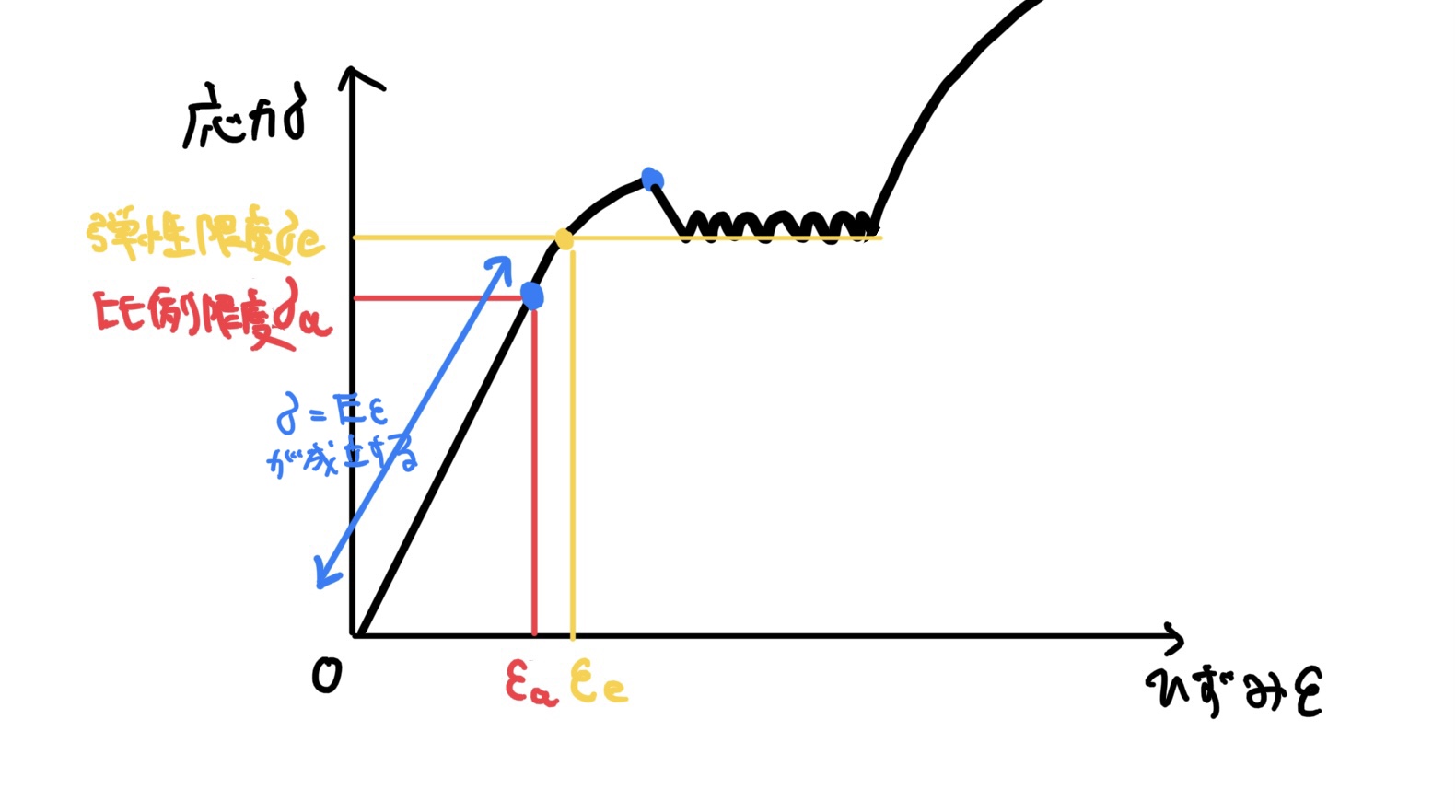
応力ー歪み線図で示された直線部分の終わりの応力をσaを比例限度と呼び、σeを弾性限度と呼ぶ。
しつこいがこの領域では、引っ張ると完全に元に戻るのだ。
次にギザギザした特性を持つ領域を説明していく。ここがメチャクチャ重要。
リューダス領域
まず言葉の定義を先のする。
グラフのギザヒザの直前の頂点の応力を上降伏点(図の①σsu)と呼ぶ。
グラフのギザギザの部分をリューダス領域と呼ぶ
グラフのギザギザの終わりの点の応力を下降伏点(図の②σsl)と呼ぶ
まずは名前を覚えてもらうため図を見て欲しい。
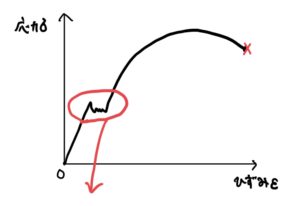
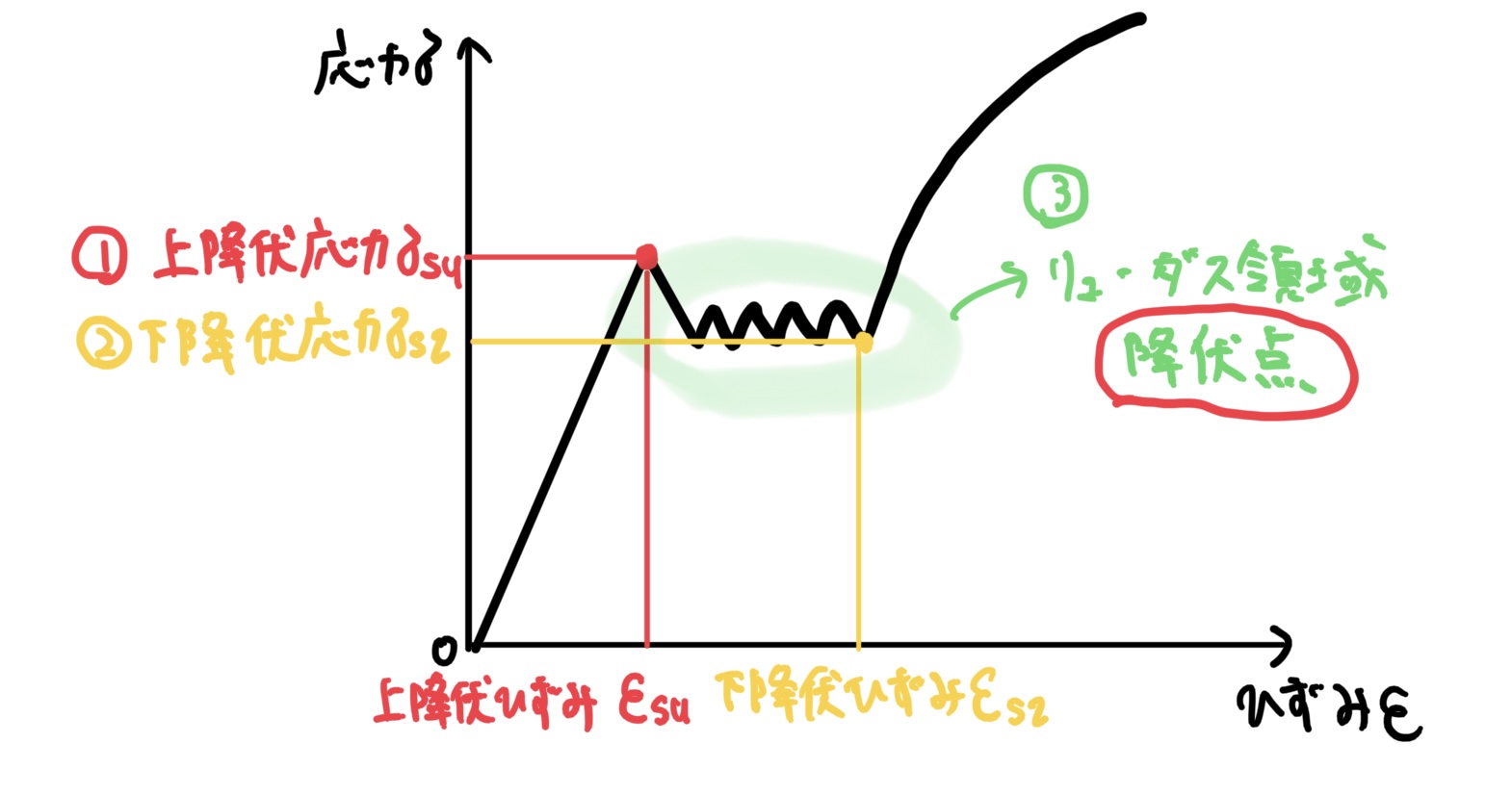
まず①から見ていこう。
座標0から応力と歪みは単純に比例して行って比例の終わりを上降伏点という。
ここまでは物体を伸ばせば元に戻る弾性域だ。
次に②を見て行こう。
②の部分はギザギザが終わって変な曲線が始まる点の応力を下降伏点という。
これ以上、歪みが増加すると当然ながら、完全に元に戻る力は失われる。
次の③のギザギザしているところの一番低い点の応力を降伏点という。
ここで何が起きているかというと引っ張る方向の斜め45度の方向で物体のすべりが発生する(破壊編で詳しく説明しているので、ここでは流してくれ)。
軸の太さの寸法を単純に考えると引っ張るので径は小さくなる(ポアソン比)のだが、実際には斜めに滑るので径が太くなるのだ。
まあ、ここで覚えて欲しいのが歪みは増加するのに応力はある範囲で一定のまま(ギザギザ)の領域があるということだ。
歪みがここまで増加すると物体が完全に元に戻ろうとする特性は失われてしまう重要な境目になる。
単純に元に戻らないのだ。
次に残った部分について説明していく。
塑性域
さらにグラフを先に進める。
ギザギザ(リューダス領域)を完全に越えて物体を引っ張ると完全に元の形に戻らない領域に入る
これを塑性域と呼び、名前が重要である
図で詳しく説明していこう
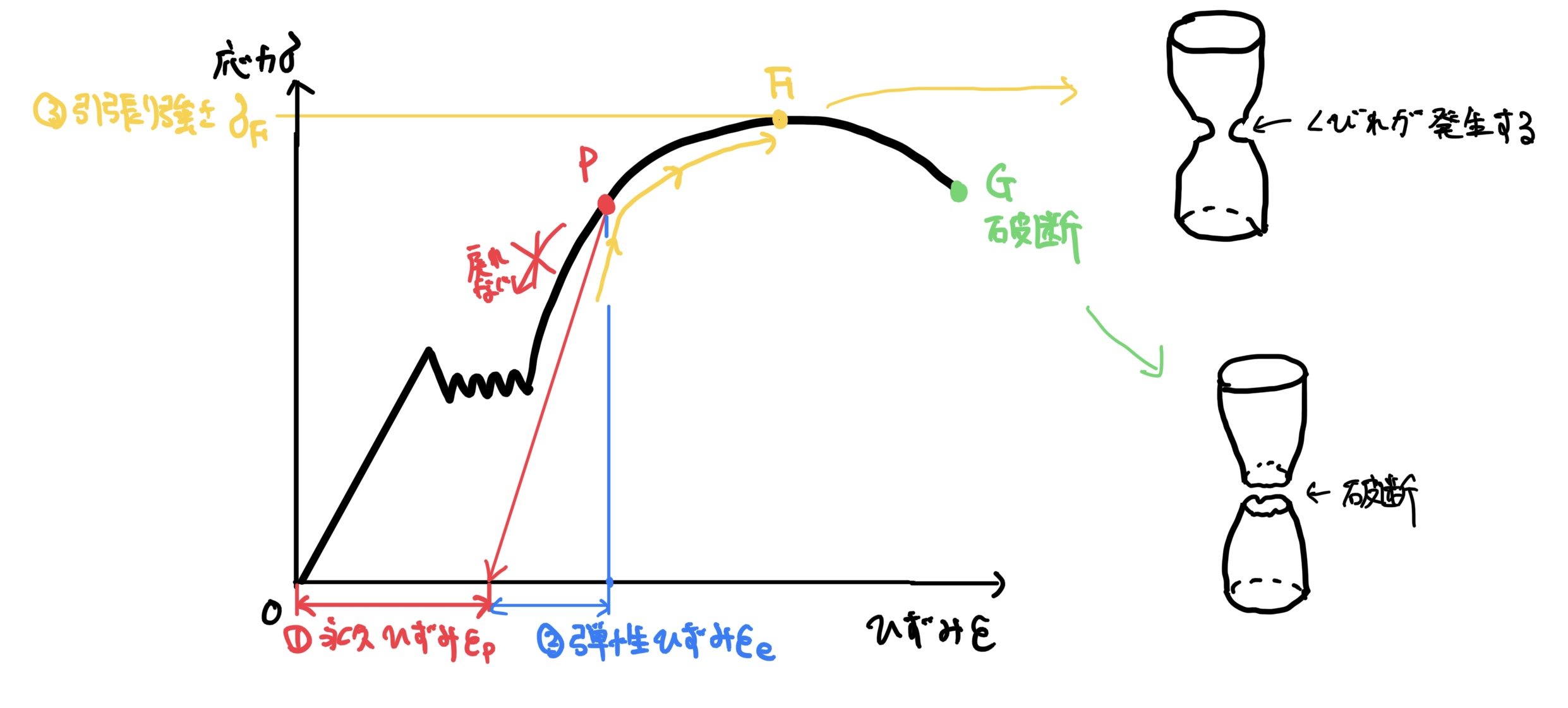
下降伏点からさらに試験片を引っ張って、例えば点Pで引っ張るのを辞めたとしよう。
弾性域であれば物体は完全な元の形に戻るのだが、ここはもう塑性域なので完全には戻らない。
その物体が完全に戻らない変形量を永久歪み(図の①εp)と呼ぶ。
しかし、実際には少しだけ元の形に戻ろうとする分があって、それを弾性歪み(図の②εe)と呼ぶ。
ここからさらに引っ張ろうとすると、弾性歪みεeに比例する係数(完全に比例するわけではない)があり、それに従って点Pに戻る。
さらにグイグイと試験片を引っ張ると試験片がくびれるように変形し始める。
この時の発生応力を引張り強さ(図の③σf)という。発生応力はこの引張り試験において最大となる。
さらに引っ張ると破断となる。
ここで面白いのがくびれ始めてから歪みは増えるのに応力は上がらない。
これは物体が勝手に硬くなり始めるのである。
自分自身が硬くなるので、勝手に強度が増していって歪みが増えても発生応力は減ってしまうのだ。
この辺の詳細なメカニズムは大学とかで研究されていると思う。
このように勝手に硬化する特性を利用して加工硬化、時効硬化などの物体の強度を上げる手法もあるが、それは別途解説する。
さらに元に戻らない領域を利用して塑性加工なんてのもある。
みんなが好きな鍛造とかプレス加工などだ(まあこれも加工編で詳細は説明する)。
ここまでが応力ー歪み線図の解説になる。
この説明した応力-歪み線図は軟鉄(粘りのある鉄)の典型例になる。
実はこの引張り試験を行えば樹脂やゴム以外の全ての材質の機械的特性がわかってしまうのだ。
ここからは物体を材質と表現して様々な材質の応力-歪み線図を紹介しよう。
代表的な材質の応力-歪み線図
ここでは代表的な材質の応力-歪み線図を紹介する。あくまで目安ね。
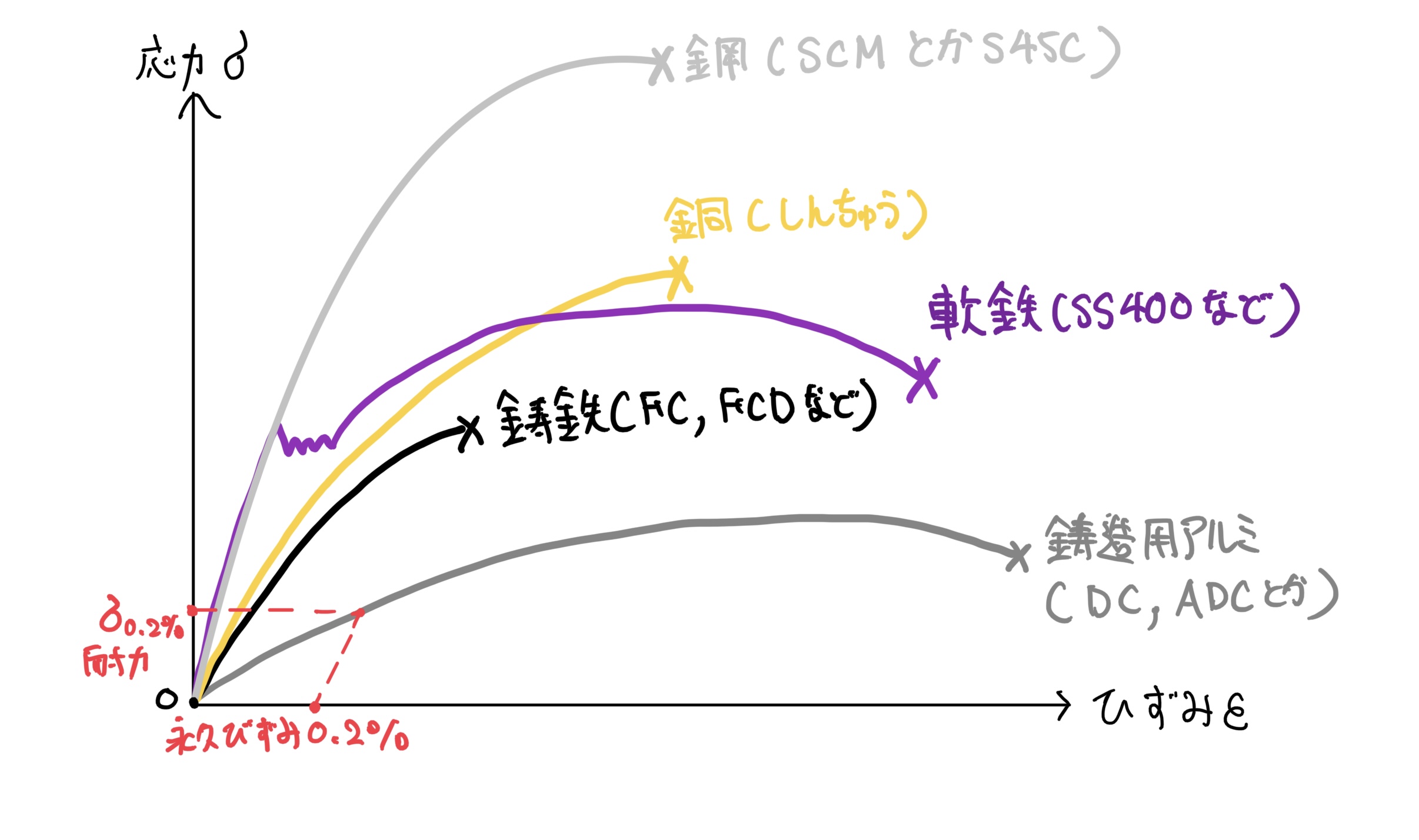
材料を比較するイメージができると思う。
またここで大切な概念が出てくる。
図を見てわかるように軟鉄以外ははっきりとした降伏点が分かりづらいと思う。
そこで使う概念が耐力である。
・物質を引っ張った時に永久歪みがごく少量だけ残るが、概ね弾性の特性を持っている領域の応力の限界値を耐力と呼ぶ
・工業の世界では永久歪みが0.2%残るのを許容して考え、その応力点を0.2%耐力点と呼び、弾性域と塑性域の境目がわかりづらい物質に対しては0.2%耐力を降伏点と同じように扱っても良い
ここまで説明すると各企業で出している材料のスペックの意味がわかるようになる。
応力-歪み線図の実践編
機械を設計するときはできたら応力-歪み線図を見て欲しい。
だが時間に追われることが多いと思うので、使う材質のスペックを見て材質の特性を頭の中でイメージすることは必ず行おう。
機械を設計するときに必ず発生する応力に対して適切な材質を選ばなければならない。
そこで基本的には下降伏点(設計ではこれを降伏点と呼ぶ)か0.2%耐力内で設計しよう。
しかしながら機械は単純の荷重を一回だけ受けて寿命を終えるということは基本的にありえない。
機械は使われ勝手によって様々な荷重が繰り返し入力される。
この繰り返して受ける荷重によって発生する応力を繰り返し応力と呼ぶ。
この繰り返し応力に対して材料が持つかどうかの判断に対して、残念ながら今回の説明では判断できない。
このような判断には応力ー歪み線図とは別に疲労限度線図、S-N線図が必要になる。
後にしっかりと説明するが超重要な疲労限度線図、S-N線図の理解に応力ー歪み線図の理解が必要になるので、良く理解しておいて欲しい。
色々と述べたがまずは基本である下降伏点=降伏点として設計しよう。

逆に塑性域で材質を使うパターンとしては試験で一回だけ持てばいい機械、単純にずっと支えているだけで応力の変化がない場合にのみ塑性域及び引張り強度で使っても良い。
また、ボルトの塑性締めとか塑性加工とか特殊な用途のみで使う(基本的に再利用する部品では使わない)。
さらに折角なので材料のスペックの簡単な例を紹介しよう。
きっと、もう各項目がどんな意味を持つかわかるはずだ。
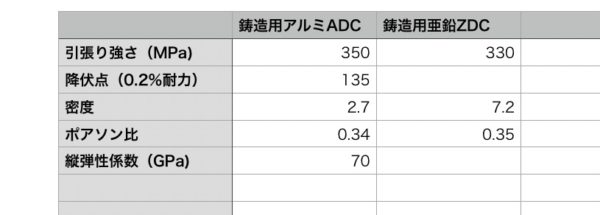
これは徐々に表をパワーアップさせていくので最初はこれで勘弁。
また、よく使う材質の物性値は別にまとめる。
さらに実践でのテクニックだが、自分の所属する企業や関連メーカーさんが新材料を提案してきたとしよう。
そのときは必ず応力-歪み線図と疲労限度線図とS-N線図を要求しよう。
これがないとまともな設計ができないのだ。
多くの場合で最初は材料の簡単なスペックしか持ってこない。
上記の資料を要求すると結構、嫌がることが多い。
でも実力のある会社なら必ず各試験を行なってデータを持っているはずである。
逆に要求しても出てこない場合は又聞きで使おうとしている材料だったり、試験がめんどくさくてやってなかったりする(試験は結構、大変)。
そういった場合は設計者の特権で、その材質の採用はなるべく見送ることを勧める。
まとめ
今回の内容は正直、多めで覚えることが多くて退屈するかもしれない。
ただその分だけ大切なことで設計者だけでなくものづくりをする人は実践で常に応力-歪み線図を利用しているはずだ。
そうでない場合はモグリに近い。
逆に言えば今回の内容がすこしでも頭に入ればあなたはもうエンジニアとしての一歩を踏み出したといっても良いと思う。
ここまでの理解で既に自信を持ってエンジニアとして仕事ができると思う。
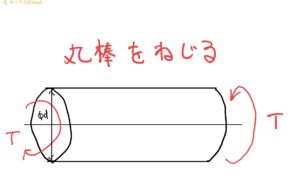
次回はねじり応力について解説していきたいと思う。
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。






コメント