これまで材料力学シリーズで様々な内力、変形の説明をしてきた。
これらは今回から始まる物体の破壊を理解するための布石とも言えるくらい破壊は大切な項目だ。
また初心者でもわかる材料力学を順に学びたい人はこちらの索引からどうぞ
機械設計だけでなくあらゆる構造物は、この材料力学の破壊の考えを基に計算されテストされて具現化されている。
とても小さなネジなどからスカイツリーみたいな巨大な建造物でも同じ考え方で計算されている。
この破壊の検討をしていない物体は、基本的にはこの世に存在しないと言っても過言ではないくらい重要だ。
つまりモノをつくることに関連する全ての人が破壊を理解していることが望ましい、いや必須で知っていて欲しい。
ここから説明を始めるが重要なことなので少々、長くなるが頑張って理解して欲しい。
破壊の理論
破壊には一応、理論らしきものは存在するが全ての破壊に対応できる一般理論は、存在しない。よって破壊の様子ごとに当てはまる理論があり、それらを材料の特性や破壊の様子に合わせて選んで適用していく。
またこの破壊の理論がなぜ大切なのかと説明すると最近では計算の主流のコンピューターシミレーション（CAEと言う）で強度計算をしたときに結果を表示するために、どんな理論で計算された結果を表示するかは人が選んで判断する必要がある。
その結果表示の判断をするために理論の概要を知っておく必要がある。
これを間違えるとCAEがいくら正確で緻密な計算をしても結果表示を間違えると大変なことになる。
この記事ではあくまで設計のための講座なので深入りはせず概要と名前だけを紹介していく。
最大主応力説
最初に最大主応力説という理論がある。
概要を説明すると外力（荷重や曲げ）が掛かっている構造物の微小な一部を取り出してその微小な一部にかかる応力を考える。
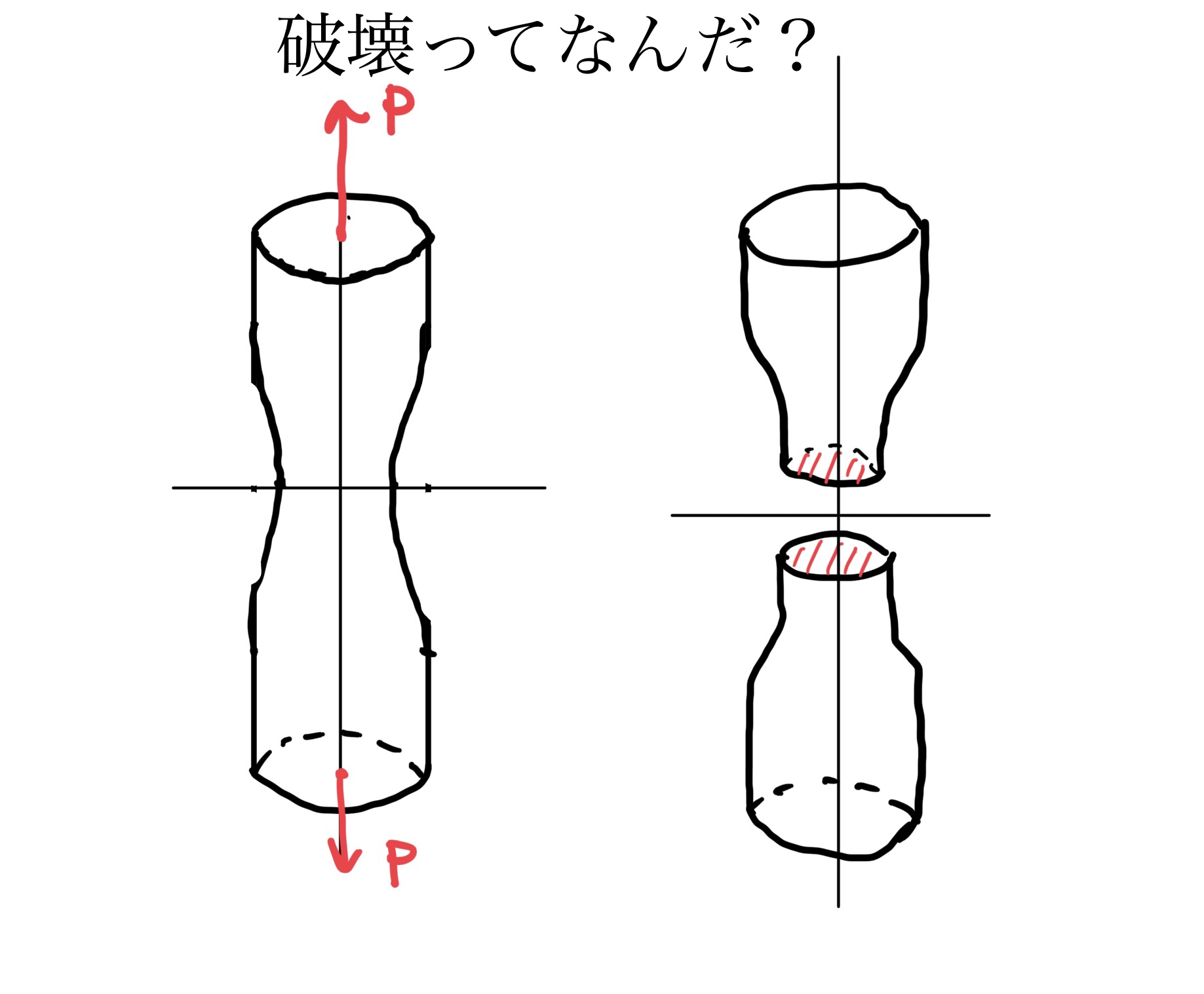
例として引張り荷重Pが掛かる丸棒から微小な形状を切り出すとその微小形状の各面には応力が発生している。
その微小な一部内にかかる応力のなかで最大応力が材料の引張り降伏点、圧縮降伏点を越えると破壊するという理論だ。
これは基本的に脆性材料（硬くて脆い奴、コンクリとか）によく合う理論なのだが延性材料（粘りがある奴、日本刀とか真鍮）や圧縮による破壊と合わないことが多い。
絶対に延性材料や圧縮が掛かっている構造物の解析で使わないようにしよう。
またCAEの結果において最大主応力では表示される応力が向きと量（ベクトル）を持っていることに注意しよう。
この詳細な内容は、3軸応力と偏微分の説明が必要なので工業数学で紹介した後に説明をする。
最大せん断応力説
最大せん断応力説は、最大主応力説のせん断力バージョンである。
概要を説明すると外力（荷重や曲げ）が掛かっている構造物の微小な一部を取り出してその微小な一部にかかるせん断力を考える。
例として引張り荷重Pが掛かる丸棒から微小な形状を切り出すとその微小形状の各面にはせん断力が発生している。
その微小な一部内にかかるせん断力のなかで最大せん断力が材料のせん断降伏点を越えると破壊するという理論だ。
延性材料（粘りがある奴、日本刀とか真鍮）や圧縮による破壊と合うことが多い。
なのでこの理論の結果表示はCAEでよく使う。
またCAEの結果において最大せん断応力では表示される応力が向きと量（ベクトル）を持っていることに注意しよう。
この詳細な内容は、3軸応力と偏微分の説明が必要なので工業数学で紹介した後に説明をする。
最大主ひずみ説
最大せん断応力説は、最大主応力説のひずみバージョンである。
概要を説明すると外力（荷重や曲げ）が掛かっている構造物の微小な一部を取り出してその微小な一部にかかるひずみを考える。
例として引張り荷重Pが掛かる丸棒から微小な形状を切り出すとその微小形状の各面にはひずみが発生している。
その微小な一部内にかかるひずみの中で最大ひずみが材料のひずみの限界値を超えると破壊する。
これは実際のテスト結果と照らし合わせるときによく使う。テストで応力を測定するときに歪みセンサーというモノを使い生のデータは歪みなので一々、応力に換算しなくても良いというメリットがある。
なのでこの理論の結果表示はテストとCAEを比べるときによく使う。
またCAEの結果において最大主ひずみでは表示される応力が向きと量（ベクトル）を持っていることに注意しよう。
この詳細な内容は、3軸応力と偏微分の説明が必要なので工業数学で紹介した後に説明をする。
全ひずみエネルギー説
ひずみエネルギーという新しい言葉が出てきてしまったがかなり簡単で便利な概念なので紹介する。
応力と歪みは、物理で習うバネの伸び（x）とバネの特性(バネ定数k)や物体の重量（m）と速度（v）が運動エネルギ($U= \frac{1}{2}kx^2. U= \frac{1}{2}mv^2 $)で表されるように歪みエネルギーという名前で表すことができる。
ここで歪みエネルギーをUとすると次の式が成り立つ。
$ U=\frac{1}{2}Eε^2=\frac{σ^2}{2E}. (ε=\frac{σ}{E}) $
この歪みエネルギーを最大主応力で説明した微小な一部にかかる3つの応力のエネルギーを算出し足し合わせることができその全部の量が微小区間で持つ総歪みエネルギーと考えることができる。
図では応力のみの歪みエネルギーを示しているが当然ながら剪断力も歪みエネルギーを持っている。
つまり微小な一部の歪みエネルギーの総和は、
$ 総歪みエネルギー＝各面の応力による歪みエネルギー＋各面のせん断力による歪みエネルギー $
となる。
この歪みエネルギーの考え方は、非常に便利で圧縮や引張りの符合つまり向き、変形の符合つまり向きを無視して歪みの量と材質の弾性係数が分かれば応力の値がわかる。
なので歪みセンサーを使ったテストの時にどのくらいの応力が発生しているのかを求めるのに非常に便利である。
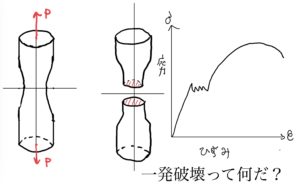
破壊の理論では引張り強度時の歪みエネルギーを応力ー歪み線図より計算してその歪みエネルギに微小な一部の総歪みエネルギーが達したときに破壊する。
この理論は、延性材料によく合う。
この歪みエネルギー説は非常に計算が楽で有用なのだが大きな欠点があってそれはCAEで結果表示される応力が量しかわからないことだ。
つまり応力の量はわかるのだが向きがわからないので引張り力なのか圧縮力のどちらなのかがわからない。
この引張り力か圧縮力の違いは、とても重要で後でしっかり説明するが荷重をかけた時の歪みの特性が全く異なりそれぞれの力に対する強度も全く異なるのだ。もう全然、別物だ。
なのでこの理論を使う時には十分に注意しよう。
歪みエネルギーの詳細に関しては偏微分などの数学知識が要求されるので工業数学を紹介した後に説明する。
せん断歪みエネルギー説
このせん断歪みエネルギー説はとても簡単で先程の全歪みエネルギー説からせん断力のみに着目して解いたモノである。
全歪みエネルギー説と同じ特性を持っており延性材料の破壊とよく合う。
このせん断歪みエネルギー説に基づいて求められた応力はフォンミーゼス応力と呼ばれる。
この応力はCAEで最も多く使われる結果の一つである。
理由としてはまずせん断力によるエネルギーのみで計算するために計算量が他と比較し圧倒的に少ない。
つまり計算量が少ないと誤差が減り、物理的な計算速度が速いので結果がすぐに出るのでよく利用される。
ただし全歪みエネルギー説と同様に応力の量のみで向きがわからない。
つまり引張りなのか圧縮なのかは、この結果だけではわからないのだ。
この向きがわからないことはよく見落としがちなので注意しよう。
材料が破壊するときの原子の様子
次に物質が破壊されるときの超ミクロな原子の動きの概要を説明する。
詳細は金属材料で説明するので、ここでは概要のみに留める。
この原子の動きのイメージを掴んでおくと材料の結晶構造や組成と強度、靭性（粘り）の関係がわかるので理解しておこう。
まずは高校化学のおさらいなのだが物質は原子と原子がたくさんくっついて分子となり存在している。
特に機械で扱うことが多い金属では金属原子特有の金属結合で構成されている。
金属結合ではある金属原子が持つ余分な電子を物質全体で共有することによって結合している。
その共有している電子$e^-$のーの電気と原子核の陽子間で働くクーロン力によって結合している。
こんな感じで金属物質はできている。
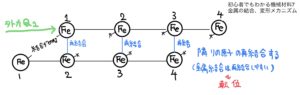
ではここに1行目の原子にせん断力を加えてみる。
そうすると原子間は結合力である程度は粘るがいずれ切れる。
分子間結合が切れると次のようになる。
面白いことに分子間結合が切れると原子はお隣の2、3、4と再結合しくっついてしまうのだ。イメージとしては原子が横滑りしていく感じだ。
これを転位と呼ぶ。
この概念が生まれたことにより材料の開発が一気に進んだのだ。
この分子間結合が粘ると靭性（伸び）が強い材料になるし逆だと脆い。
では、脆いと全てダメなのかというとそうではなく逆に転位を起こしやすいので加工性がとても優れた材料になる。
特に切削加工やプレス加工に向いた材料となる。
靭性に優れる材料は、部材として強度などで優れた特性があるが転位を起こしにくいので加工しにくい。加工するなら鍛造とかになってしまう。
要は性能とコストのバランス、使い所の問題なのである。
また鉄やアルミなど多くの材料は様々な添加物（モリブテン、炭素、シリコンなどたくさん）を加えたり、熱を与えたり冷却したりすることで結晶構造や分子間結合を変化させ様々な特性を持つ材料に加工される。
この概念は非常に大切なので理解しておこう。
引張りに関しては単純に原子の結合力に打ち勝つ力を加えて結合を切るだけなので単純である。
転位ついて詳しく知りたい方は良かったらこちらを覗いて見て欲しい。
-
-
初心者でもわかる機械材料5 金属の結合、変形メカニズム、超重要！！(クーロン力、転位、変形）
まとめ
破壊をまとめると
破壊理論のまとめ
・破壊の理論は主に5つある。最大主応力説、最大せん断応力説、最大主歪み説、全歪みエネルギー説、せん断ひずみエネルギー説だ。
・最大主応力説は、脆い材料によく合う理論である。靭性のある材料では使わないこと。
・最大せん断応力説は靭性のある材料によく合う理論である。
・最大主歪み説は歪み量を基に考えるのでテストと照らし合わせるのに便利である。
・全歪みエネルギー説は計算量が少なく計算しやすいが算出した応力の向きがわからなことに注意。
・せん断歪みエネルギー説は最も計算量が少なくて済む理論であり頻繁に利用される。
・せん断歪みエネルギー説で算出した応力はフォンミーゼス応力と呼ばれよく利用するが向きがわからないことに注意。
・物質が破壊されるときに転位という原子間の横滑りが発生する。
になる。
いつもに比べ少し量が多いがとても大切なことなので良く理解して欲しい。
特に昨今では自分で計算することはほとんどなくシミレーション（CAE）で計算するのが主流である。
ただしCAEは、計算するだけでどの破壊理論を適用するのか、物理現象と合っているのかを判断するのは人間である。
適切な判断を下すためには理屈を知っていないと間違えてしまい実際に使用してみたらあっさり壊れたなんて話は、頻繁に存在する。
少しの手直しで修正できるのであればまだ良いが土台のようなところで間違えると全部やり直しになってとんでもないことになる。
また他人が計算した結果を見るときにまずどの理論で計算したのかを把握しないと見ることすらできないし判断も無理である。
ちょっとした計算ミスより適用理論の間違えのが遥かに恐ろしいのだ。
このようにAIやシミレーションが加速度的に発展している今だからこそめんどくさいが理論をよく理解して欲しい。
次回はより具体的な破壊の考え方について紹介する。
-
-
初心者でもわかる材料力学19 一発破壊、引張り強度編（応力歪み線図、リューダース線、破断面)
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める（漫画〜専門書まで幅が広い）。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験（機械設計者の転職活動）を共有できるように記事に起こしたので参考にして頂ければ幸いだ。
-
-
転職活動シリーズ1 私の転職活動概要（機械系エンジニア、３０代半ば2010年代の中頃）
続きを見る
