前回までで材料力学中盤のハイライトであるはりのたわみの説明がひとまず終わった。
これまで材料を引っ張る、捻る、撓む変形を紹介して来た。今回から始める説明の変形は押す、潰すを紹介しこれで主要な材料の変形は一通り説明したことになる。
この引っ張る、捻る、撓む、潰す(圧縮)の変形がわかればどんな構造物の変形も一つ一つ分解していけば基本的に4種類の変形の組み合わせになる。
さらにこれから説明していくが同じ材質、サイズでも引張りで荷重を受ける場合と圧縮で荷重を受ける場合では条件にもよるが圧縮で受けた方が材料が強い場合が多い。賢い設計者はうまく圧縮で部材を使うことが多い。
よて効率の良い設計のためにも非常に重要な変形の一つなので是非、理解して欲しい。
またこの圧縮による変形に関しては、歴史が長いが厳密にはよくわかっていないこともあって実験式を使う場合があるのでご了承願いたい。
座屈ってなんだ?
いつも通り座屈を説明する前にイメージを統一しよう。
まず平な地面に短い丸棒が立っていてその棒を上から超強い力で押すとどうなるだろう。そう。潰れて太るよね。
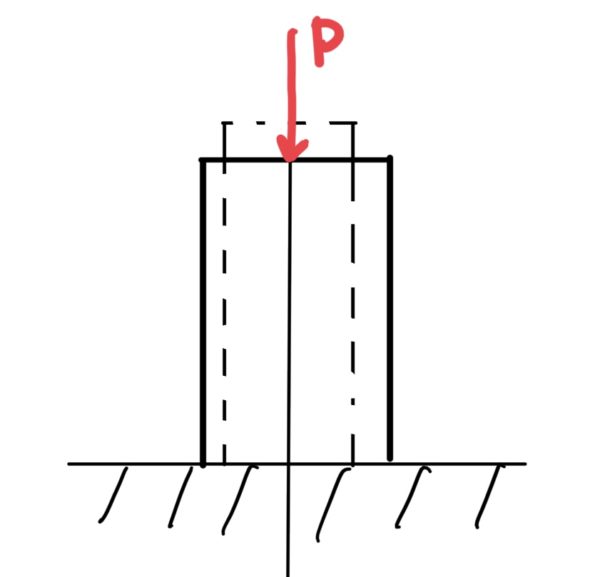
では次にそこそこ長い丸棒を超強い力で押すとどうなるだろう?
完璧な円でできた1μいや0.001μ以上の精度でできた円柱で寸分の狂いもなくど真ん中を押せればそのまま潰れるかもしれない。
でもそんなものはこの世に存在しない。長い丸棒を押すと押しているうちにある力の所で棒がくにゃっと曲がる。長さによって変わるけど単純にくの字に曲がったり、S字のような曲がり方をするかもしれない。
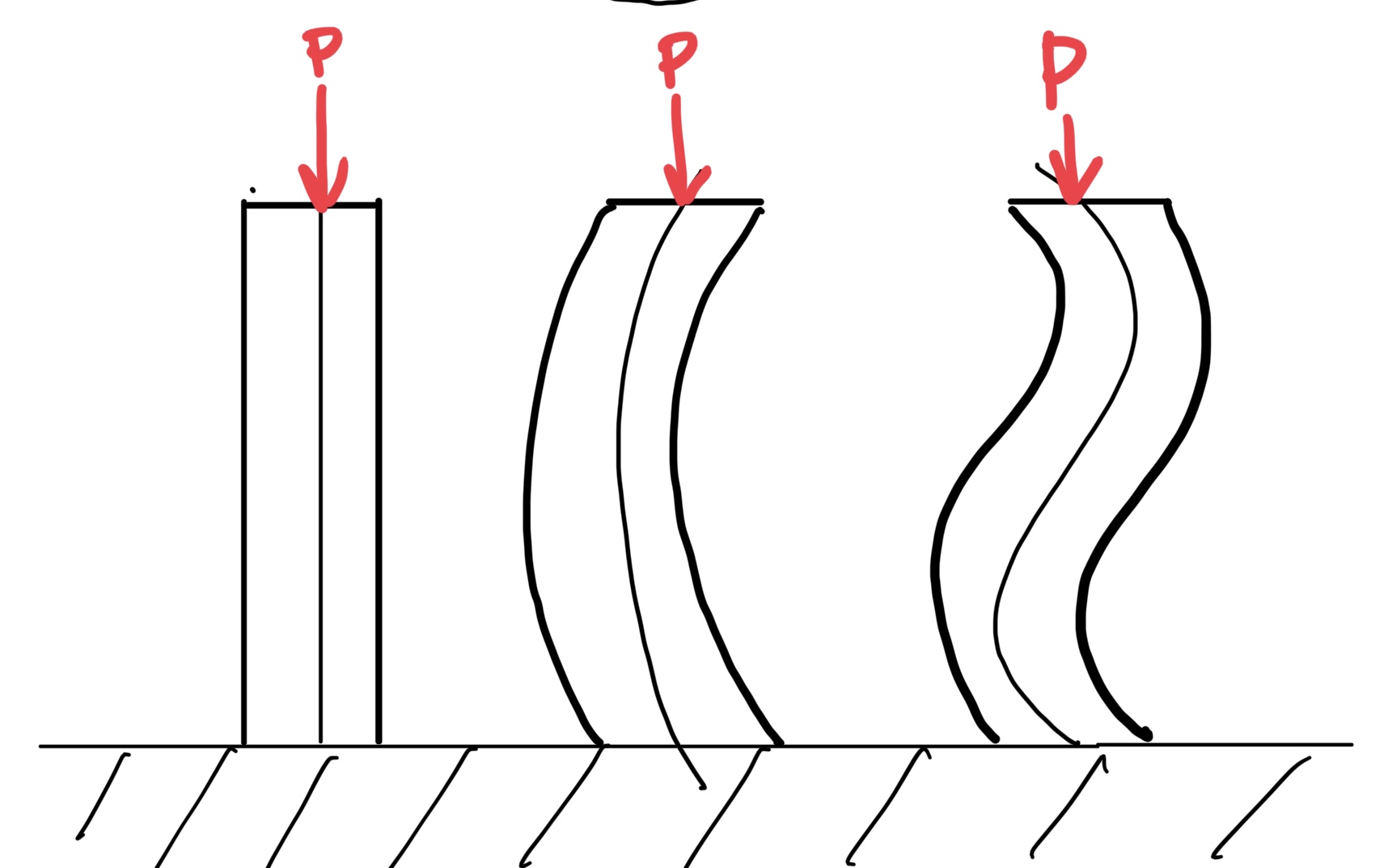
そう、この丸棒を長柱と考えてくにゃっと曲がる変形を座屈という。さらにこのくにゃっと曲がるときの荷重を臨界荷重と呼ぶ。
また“くの字“の変形の曲がる点を節といい。節の数でS字とかそれ以上に曲がる状態を表現する。
これは柱の太さや長さ、掛かる圧縮力によって変形の形態は変わる。
もう少し厳密な座屈のイメージを考えよう。
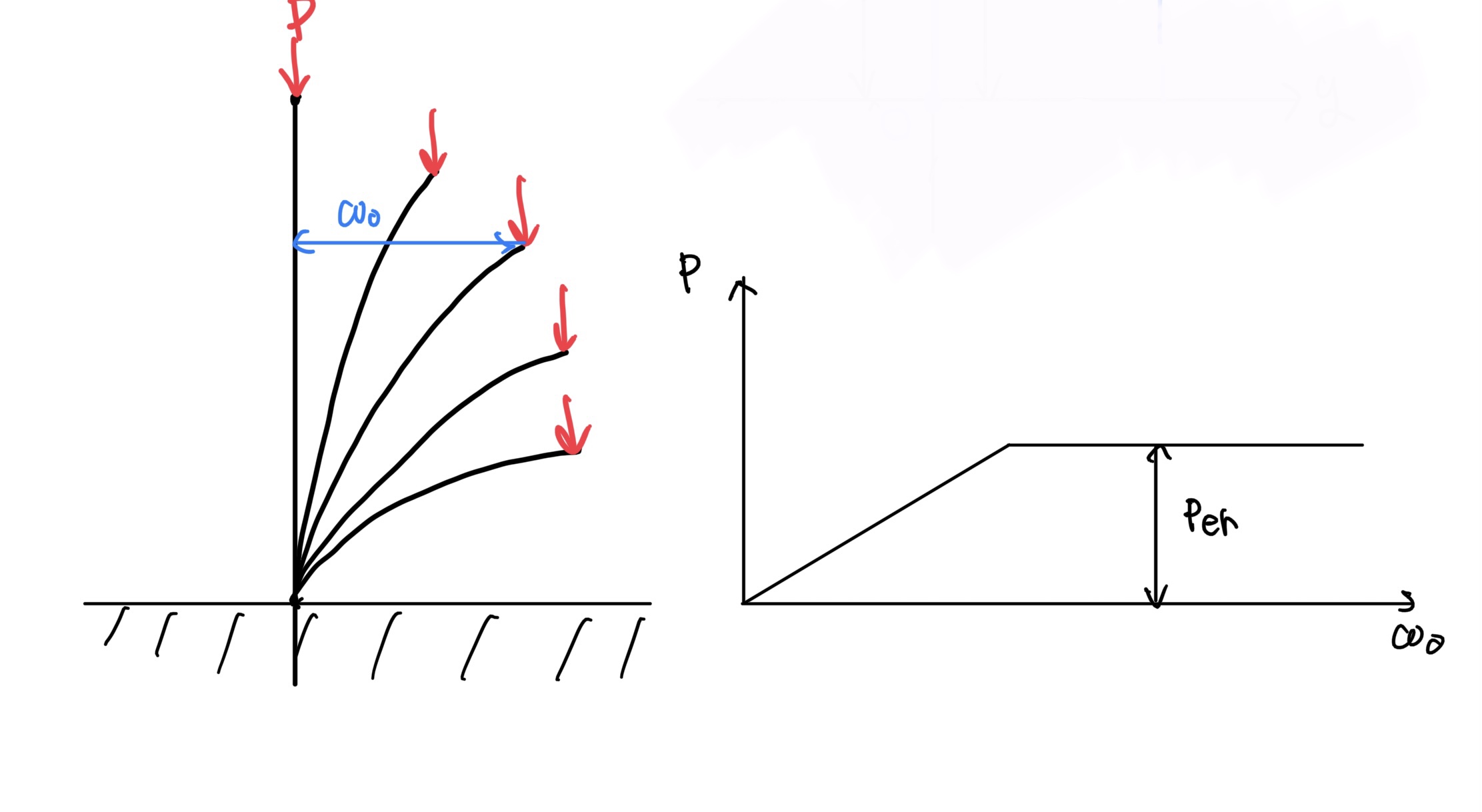
ではイメージ合わせの最後にくの字に曲がる場合にどんどん荷重をかけていった場合にどうなるか図で示す。棒がくの字に変形すればするほど荷重点が離れていく、その距離をここではω0(オメガ)で荷重はPとする。
どんどん荷重を与えてくの字にするとある程度のところで荷重を増やさなくても撓んでいき(柱が撓んで勝手に曲げモーメントが増加する)、材料によっては、ぼちぼち引張り強度に達して破断する。この現象も座屈と言われこのときの荷重を座屈荷重Perという(グラフのPer)。
簡単にまとめると細くて長い棒が立っていてその上から押したら棒は、くにゃっと曲がってその内に折れる。
小学校の実習で園芸で使う棒とかを固い地面に刺そうとして曲げて折った経験があると思う。しかも曲がったら急に力が抜けた感じを受けたと思う。(みんな、いたずらしたことあるでしょ。)
それがさっき説明した掛かっている荷重よりたわみの変形が大きすぎて急に棒が折れるのですっと力が抜けた感じになる。
これが典型的な座屈で園芸の棒が折れたときの荷重が座屈荷重になる。
これで座屈の雰囲気は掴んでもらえたと思う。次にたぶんみんなが嫌な式を立てていく。
弾性座屈とオイラーの公式
では座屈の式を立てるためにいつも通り例題を設定する。
まず大まかな例題のイメージとしては長い柱を荷重Pで押して変形した状態を考える。座屈を考える時は座標を柱の中心ではなく柱の左端に原点を置く(荷重点Pの偏心量を考慮するため)。座標を図示すると図の黄色いところ。だから荷重Pはちょっと偏心した点になる。
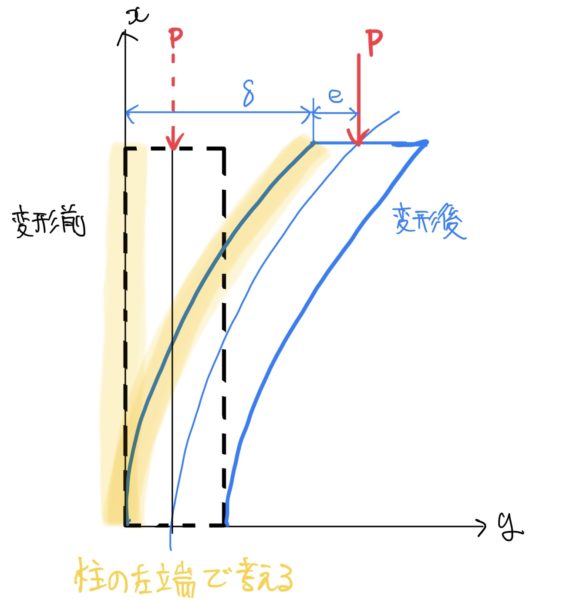
さらに例題を詳細に設定していくと平な地面から長さlの柱があり、柱の先端に荷重Pがかかり節が1点で撓んだ状態を考える。座標は柱の根元を原点とし縦方向を+x、図の右方向を+yとする。また荷重点は柱のたわみ量δ(デルタ、Δの小文字)とし偏心量をeとする。
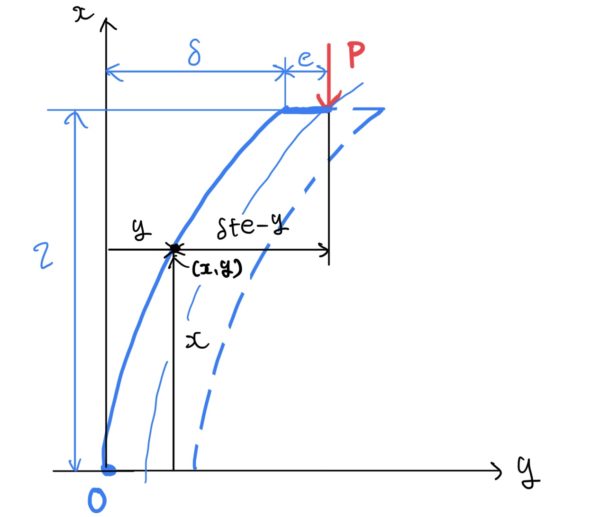
ここからは今までやってきた片持ちはりのたわみと一緒で荷重Pの位置が多少めんどくさいがたわみの微分方程式で解いていく。
いつも通り十分な長いはりの場合は剪断力を無視して曲げモーメントを求めていくと荷重Pと偏心量eのーPe(撓む方向に逆らうので−)なのだが既にδ(デルタ)ほど撓んでいるので厳密には任意の座標(x,y)での曲げモーメントMは次の図のようになる。
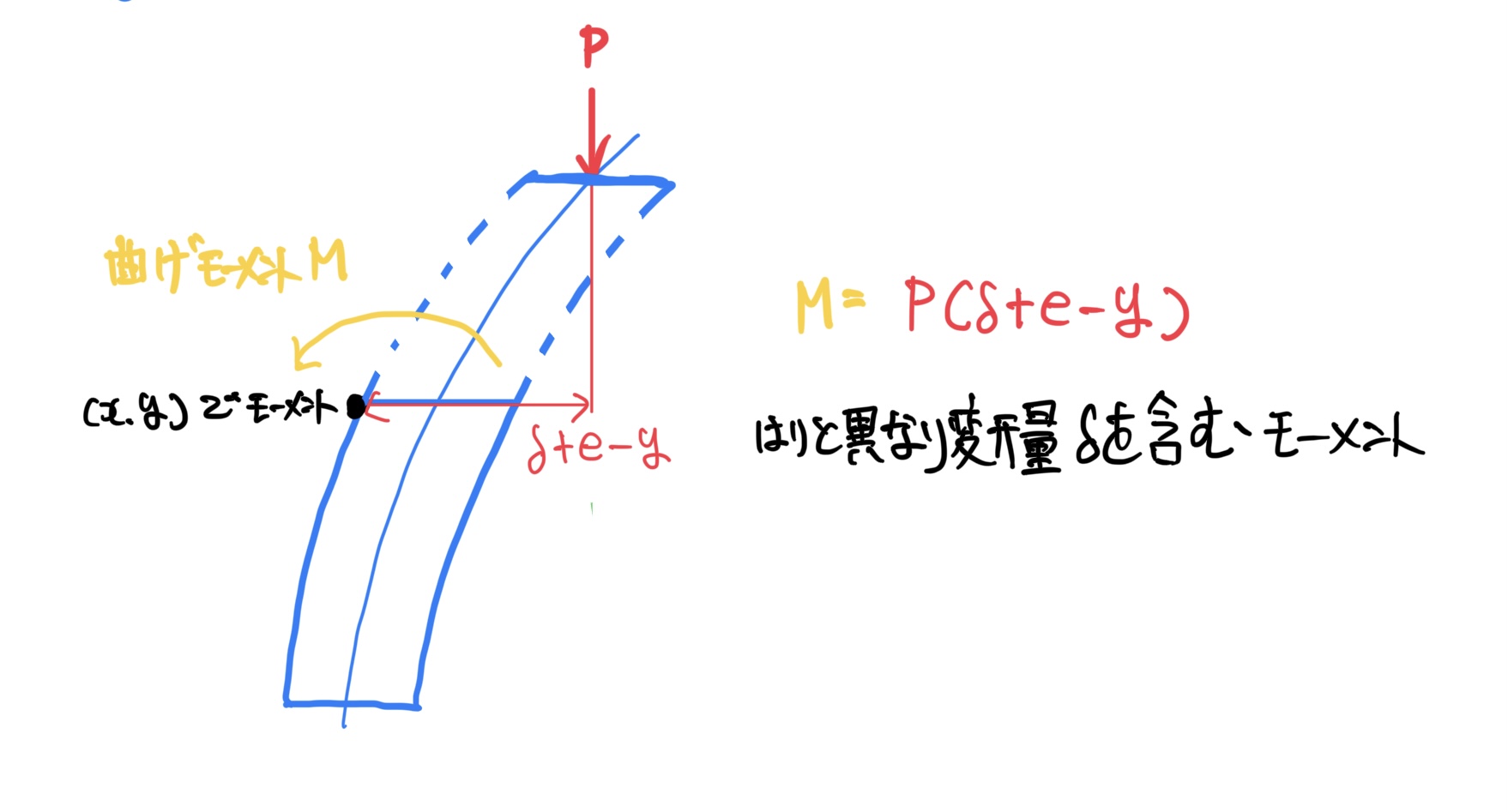
ここでのポイントははりと異なり変形量δを考慮して曲げモーメントを考える。
$ 曲げモーメントM=P(δ+e-y) $
後は、これを撓みの部分方程式に代入すれば良い。代入すると次式になる。
$ \frac{d^2y}{dx^2}=\frac{P}{EI}(δ+e-y) $
ここで定数になる$ \frac{P}{EI}=α^2 $と置くと次のようになる。
$ \frac{d^2y}{dx^2}+α^2y=α^2(δ+e) $
この微分方程式を解くのだが今までのようにただ積分しただけでは、変数yがいるので求まらない。
ここで数学のテクニックを使って解く。このサイトの趣旨としては数学のテクニックを使わずに解説したいが因数分解、微分、積分にもあるように微分方程式を解くのにも特殊なテクニックがいるのでしょうがない。この微分方程式についてはページの後半で少し解説するので今のところは先に進めていく。
では解いていく。上式の微分方程式の一般解はA、Bを定数として次の式で表される。
$ y=Asin(αx)+Bcos(αx)+δ+e $
$ \frac{dy}{dx}=Aαcos(αx)-Bαsin(αx) $
で求められる。
ここで境界条件は下端が固定されているので
$ x=0でy=0、たわみ角θ\frac{dy}{dx}=0 $
よりA=0、B=-(δ+e)になり微分方程式は、
$ y=(δ+e)(1-cos(αx)) ・・・・① $
一方で長柱の上端は、
$ x=lでy=δ $
となりそれぞれの定数は、
$ A=0、B=-e\frac{1}{cos(αl)}、δ=e(\frac{1}{cos(αl)}-1) $
となりこれらを微分方程式の解に代入すると
$ y=\frac{e(1-cos(αx))}{cos(αl)} $
となる。
これで柱のたわみ量がわかる。
次にこの式の意味を考えていこう。
着目するのは式の分母でcos(αl)が0になるとたわみ量は♾️になってしまう。たわみ量が♾️だと柱は完全に壊れてしまう。
ではcos(αl)が0になるのは下のグラフのように+側で見ればθが$ \frac{π}{2}, \frac{3π}{2}・・・ $で0になる。
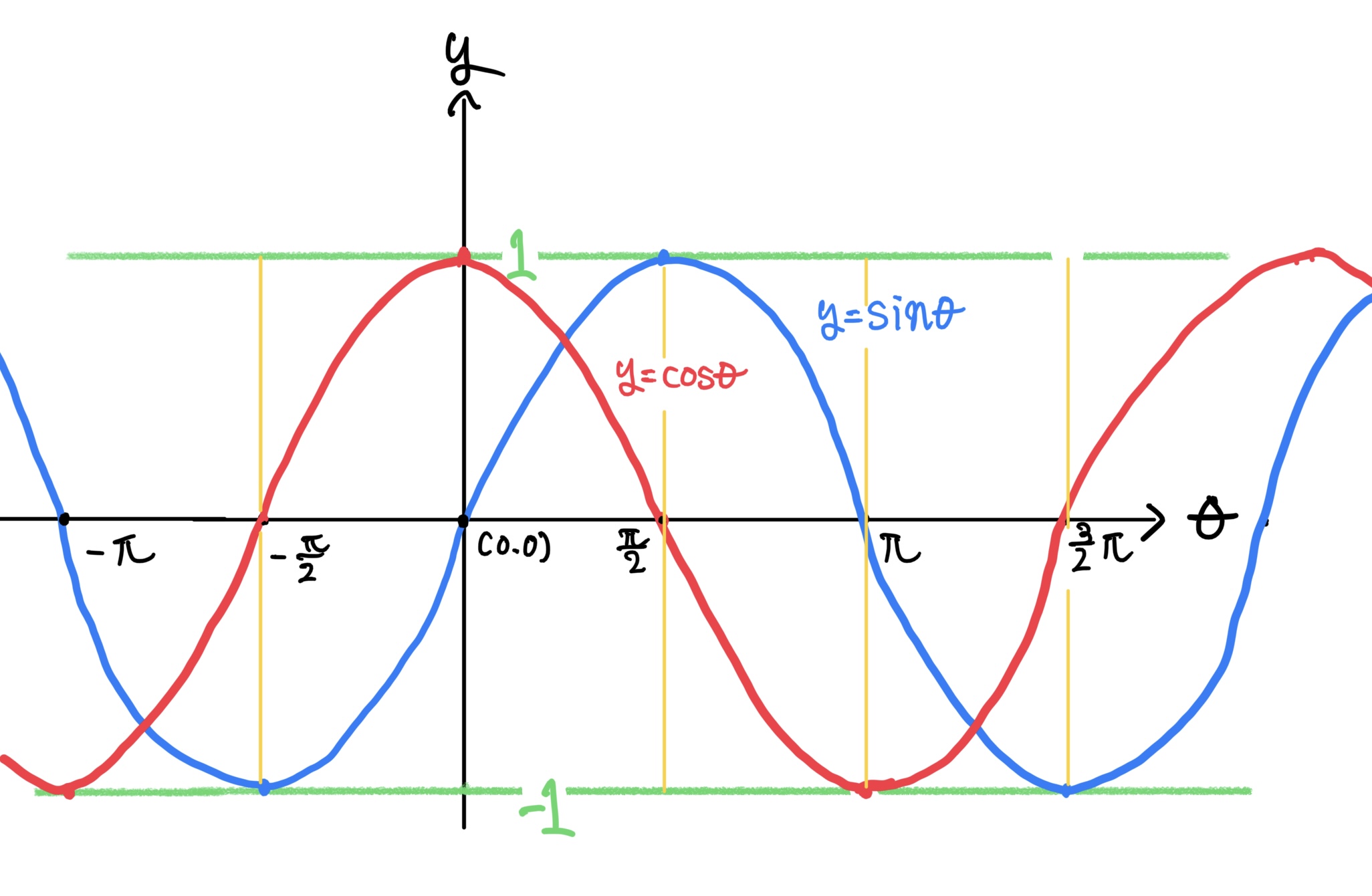
cos(αl)が0になる時は分子が奇数なので奇数をm+1と置くと、
$ αl=(2m+1)\frac{π}{2}, (m=0,1,2,3,….) $
この条件の時にたわみは無限になり柱は破損する。
次に偏心量eが0の時を考えてみよう。
偏心量eが0でも柱がたわむ(潰れて太るのではない)と考えると先程のたわみの途中の式①$ y=(δ+e)(1-cos(αx)) $が成り立つのでこの偏心量eを0にすると
$ y=δ(1-cos(αx)) $
で長柱の上端(x=l)のたわみはδなので
$ δcos(αl)=0 $
δは上端のたわみなので0に歯ならないのでcos(αl)が0になる。
そう結局、偏心量eが0でもcos(αl)=0になる運命でその時のたわみはもちろん先程、求めた式から無限になり破損する。
では柱が壊れる条件αl=0の時はとのような荷重になるのか求めていこう。
αを元に戻すと
$ \frac{P}{EI}=α^2 $と$ αl=(2m+1)\frac{π}{2}, (m=0,1,2,3,….) $より
$ P=(2m+1)^2\frac{π^2EI}{4l^2}、 (m=0,1,2,3,……) $
$ P1=\frac{π^2EI}{4l^2}、 P2=\frac{9π^2EI}{4l^2}、…..$
となる。
つまり上式で求めた荷重の時に柱のたわみが無限となり破壊する荷重となる。
この式の最小の解$ P1=\frac{π^2EI}{4l^2}=Per $を一端固定、他端自由の座屈荷重Perという。
式を見れば座屈荷重の特性がわかると思うが長さが長くなると二乗で荷重が小さくなる=すぐ座屈する。弾性係数、断面2次モーメントが高いと座屈荷重は大きくなる=丈夫になる。
逆に偏心量と材料自身の強さには全く関係せずに破損する面白い特性を持っている(幾何学的に強度が決まる)。
これを上手く利用すると断面2次モーメントが大きく短い柱で支えると材料の種類関係なしに丈夫な構造物にできる。これでしょぼい材料しか使えない場合にこのテクを用いると信じられないくらい強い構造物が設計できる。ここが設計の腕の見せ所なのだ
ここで荷重がm=0、1、2、3・・・と複数あることに疑問を持つと思う。これはどういう意味かというと次の図を見て欲しい。
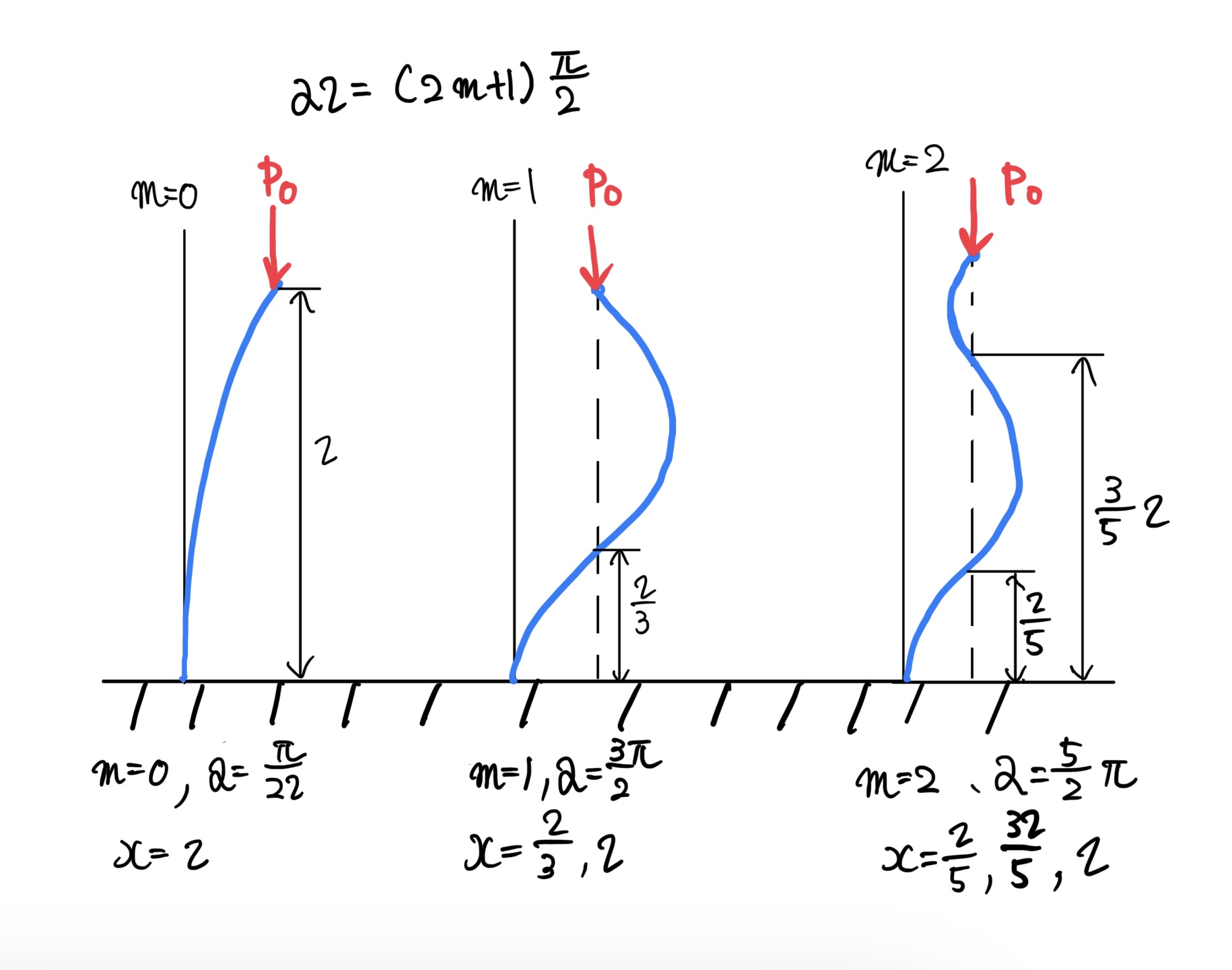
そう破壊される時の変形の形が変わるのだ。これを座屈の変形モードと呼びm=0、1、2を0次、1次、2次と呼ぶ。
基本的にはm=0で破損することが多いのでこれで見ておけば良いのだが長柱の断面と長さから意外とm=0を耐えてm=1、m=2で破損することもある。
筆者の場合は過去に似たうような形での破壊試験を探して結果を見てmの値を決めることが多い。
またいつも使う部品で座屈計算をしなければならない時に大抵のまともな会社なら何次のモードで計算するのかデータがあるはずである。
もしなければ座屈の試験をして座屈形のモードを調べておくことが望ましい。筆者だったらまず実験する。
なぜなら何でもかんでも変形モード0次の荷重で計算すると弱い荷重で設計するので巨大で重たい設計になってしまう。そんなものは市場競争力がないだろうしコストもかかるので良くないのだ。
たわみの2回線系微分方程式
材料力学、座屈とは関係がないが折角なので$ \frac{d^2y}{dx^2}+α^2y=α^2(δ+e) $の一般的な解き方を軽く載せて置く。
$ \frac{d^2y}{dx^2}+α^2y=α^2(δ+e) $は一般解と特解が存在するのでそれぞれを求めて行こう(y’’、y’、y以外の定数があるので特解が存在する)。
まず右辺の$ α^2(δ+e) $は置いといて$ \frac{d^2y}{dx^2}+α^2y=0 $を解いて一般解を求めよう。
面倒なので$ y’’+α^2y=0 $に書き換える。
数学の先生や詳しい人に怒られそうだが微分方程式にy、y’、y’’が混ざっている式だとyを次のように仮置きすると上手く解ける事が多い(y’=yで$ y=e^(x+c) $のように基本的に指数関数になるから)。
$ y=e^λx、y’=λe^λx、y’’=λ^2e^λx $
これを$ y’’+α^2y=0 $に代入すると
$ λ^2e^λx+α^2e^λx=0、(λは適当) $
式を解くと指数関数は0にならないので$ λ^2+α^2=0 $になる。これでλは$λ=±αi(i:虚数)$の2つの解を持つので$ y’’+α^2y=0 $の解は次のようになる。
$ y=C1e^{αx}+C2e^{-αx}、(C1、C2は積分定数)$
オイラーの定理$ e^ix=cosx+isinx、e^-ix=cosx-isinx $を使って表すと
$ y=(C1+C2)cosαx+(C1-C2)isinαx $
ここであまり上手い方法ではないが解が虚数になる事がないのでC1とC2を弄って虚数iを消す。C1とC2を共役関係にしてしまう。
$ C1=A+Bi、C2=A-Bi $
これでyは
$ y=2Acosαx-2Bsinαx $
次に特解を解いて行く。
特解は$ α^2(δ+e) $に倣って変数を持たないので仮に定数y=Cと考える。
これを最初の微分方程式に代入すると
$ \frac{d^2y}{dx^2}+α^2y=α^2(δ+e) 、α^2C=α^2(δ+e)、C=(δ+e) $
これで一般解と特殊解から微分方程式が次のように解ける。
$ y=2Acosαx+2Bsinαx+(δ+e) $
こんな感じで解ける。
線形微分方程式、一般解、特殊解、虚数、オイラーの定理といろいろな大切なキーワードが出てきたが今回は材料力学なのでスルーして進めた。どれも大事な概念なので別ページの工業数学で説明するので待って欲しい。
ちなみにこの形の$ \frac{d^2y}{dx^2}+Ay=B $の微分方程式は工業でよく使われるので重要だ。
まとめ
今回で座屈の基本を説明した。
途中の微分方程式を解くときに多少、特殊なことをする必要があるが今は流し見で結果に着目してほしい。
まとめると
・座屈荷重は、$ P1=\frac{π^2EI}{4l^2}=Per $で求められる
・座屈荷重は荷重の偏心量、材料の強さに全く依存しない。
・座屈には変形モードがあり何次のモードで破損するのか解った上で計算しよう。
次回は両端固定の場合、両端自由の場合の座屈荷重を求めていく。またできたら実験式の紹介まで進みたい。
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。






コメント