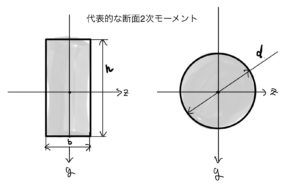
前回は代表的な断面二次モーメントを説明した。
今回は代表的なはりのたわみを紹介する。
機械構造物は単純化すると複数のはりが組み合って構成されていると言っても過言ではない。よって強度計算を行う場合にはりの問題は避けて通れないのだ。
さらに機械を設計するのに強度計算は避けられない。つまり常に使われる大切な考え方であると言える。
ただし全てが自力のみで解ける必要はない。意味を理解しておいて忘れたら調べれば良いだけである。意味についてはこれまでのページを参照して欲しい。
ここからははりのたわみの意味を理解した上で代表的な解を紹介していく。
代表的なはりのたわみ
ここからの説明では全て一様な断面を持つ(断面二次モーメントIとする)弾性係数がEのはりとする。座標ははりの左端部を原点とし下方向が+yで右方向が+xに統一する。
複合材などを求めるときはこちらを参照して等価断面の断面2次モーメントにすればこれから紹介する結果は全て使える。
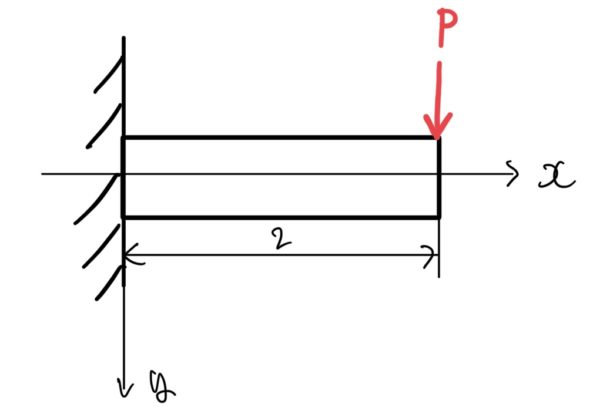
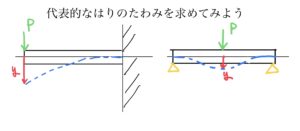
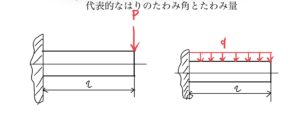
はりの先端に荷重を受ける片持ち支持はり
はりの先端に荷重Pを受ける片持ち支持はりのたわみ量y、たわみ角θ
$ たわみy=\frac{Pl^3}{6EI}(3-\frac{x}{l})\frac{x^2}{l^2} $
$ 最大たわみymax=\frac{Pl^3}{3EI} (x=l) $
$ たわみ角θ=\frac{Pl^2}{2EI}(2-\frac{x}{l})\frac{x}{l} $
$ 最大たわみ角θmax=\frac{Pl^2}{2EI} (x=l) $
これははりのたわみの基本形でかなりよく使う。
実際には軸の先端にギヤが付いていてそのギヤがあるトルクで廻る時に反力として軸に荷重がかかり片持ちはりのようになる。
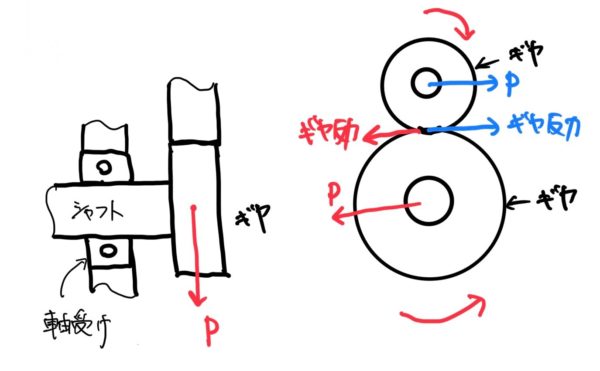
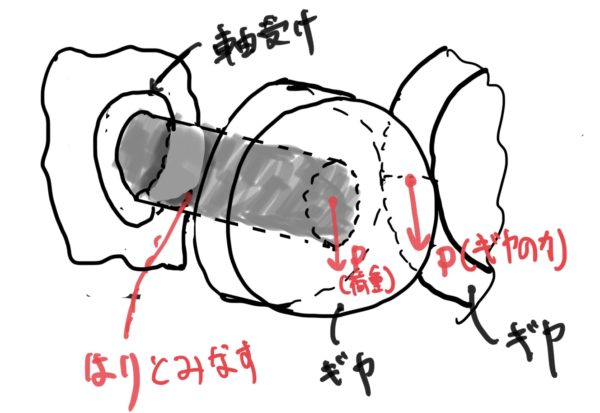
たわみも重要だが軸受の寿命計算をするのにはりの根本の荷重が必要だったりする。
等分布荷重qを受ける片持ちはり
等分布荷重q(N/mmなど)を一様に受ける片持ちはりのたわみ量y、たわみ角θ
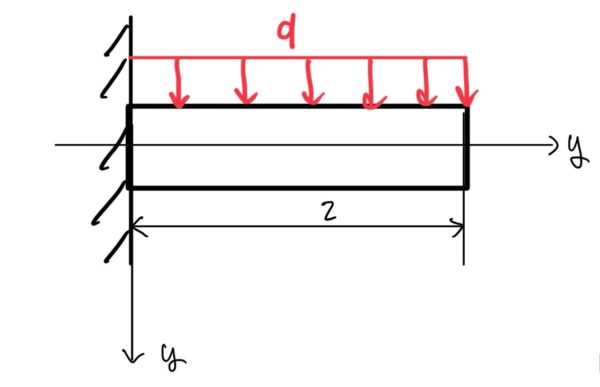
$ たわみ量y=\frac{ql^2}{24EI}x^2(6-4\frac{x}{l}+\frac{x^2}{l^2})$
$ 最大たわみ量ymax=\frac{ql^4}{8EI} (x=l) $
$ たわみ角θ=\frac{ql^2}{6EI}x(3-3\frac{x}{l}+\frac{x^2}{l^2}) $
$ 最大たわみ角θmax=\frac{ql^3}{6EI} (x=l) $
これは流体を受け止める部材に適用できるはりだ(圧力を受ける)。
リードバルブ、リリーフバルブと呼ばれる機械要素で穴と穴を塞ぐ板バネで構成されていて板バネが圧力を受けてたわむと穴に隙間ができて流体が流れる。
つまり圧力によって作動する可動蓋みたいなものだ。
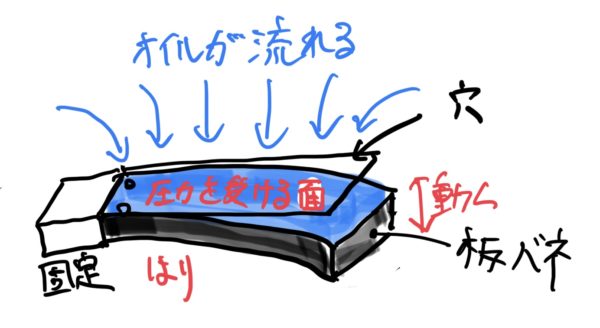
これは筆者の専門のエンジンでは必ず付いている。また日常的にも気づいていないだけで台所、お風呂、洗面所などの水まわりでよく使われていると思う。
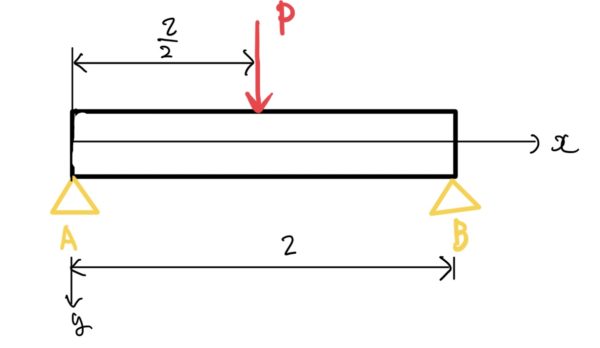
はりの中央に荷重Pがかかった両持ちはり
はりの中央$ \frac{l}{2} $に荷重Pが掛かる両持ちはりのたわみ量y、たわみ角θ
$ たわみ量y=-\frac{Pl^3}{96EI}(\frac{x^3}{l^2}-3x)、(x≦ \frac{l}{2}) $
$ たわみ量y=-\frac{Pl^3}{12EI}(1-\frac{l}{x})(\frac{x^2}{l^2}-2\frac{x}{l}+\frac{1}{4})、(\frac{l}{2}≦x) $
$ 最大たわみ量ymax=\frac{Pl^3}{48EI} (x=\frac{l}{2}) $
たわみ角の一般式は省略する。
$ 最大たわみ角θmax=\frac{Pl^2}{16EI} (x=0,l) $
これは軸の真ん中にギヤが付いていたり、台の上に物体を乗せたりとか普通の生活でもよくあるものなので実例の紹介はしないが重要だ。
はりの両端にモーメントMがかかっている場合の両持ちはり
はりの両端にモーメントMが向かい合う方向で掛かっている両持ちはりのたわみ量y、たわみ角θ
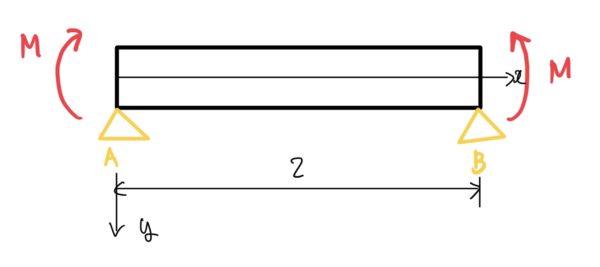
$ たわみ量y=\frac{M}{2EI}x(l-x) $
$ 最大たわみ量ymax=\frac{Ml^2}{8EI}、(x=\frac{l}{2}) $
$ たわみ角θ=\frac{M}{2EI}x(l-2x) $
$ 最大たわみ角θmax=\frac{Ml}{2EI} (x=0、l) $
これもよく使うはりのたわみだ。
例えば二つの離れた壁をリブで繋いで補強する。壁が何かの力を受けて倒れてくる。壁の倒れによりリブが強制変形させられモーメントがかかる。
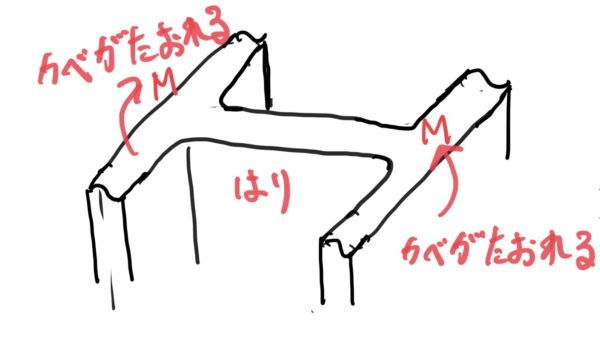
よく考えると身近にもたくさんあると思う。例えばホームセンターで売っているコンクリートブロックの一部分がこの形が多いと思う。
等分布荷重qを一様に受ける両持ちはり
等分布荷重q(N/mm)を一様に受ける両持ちはりのたわみ量y、たわみ角θ
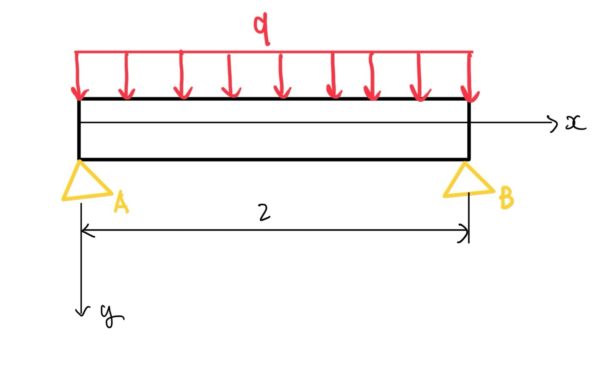
$ たわみ量y=\frac{ql^4}{24EI}\frac{x}{l}(1-2\frac{x^2}{l^2}+\frac{x^3}{l^3}) $
$ 最大たわみ量ymax=\frac{5ql^4}{384EI}、 (x=\frac{l}{2}) $
$ たわみ角θ=\frac{ql^3}{24EI}(1-6\frac{x^2}{l^2}+4\frac{x^3}{l^3}) $
$ 最大たわみ角θmax=\frac{ql^3}{24EI}、(x=0、l) $
これは流体を受ける蓋などがこのタイプだ。完全に同じはりとして扱えないが容器の底の部分とかはこの考え方だ(実際には面なので計算が面倒)。
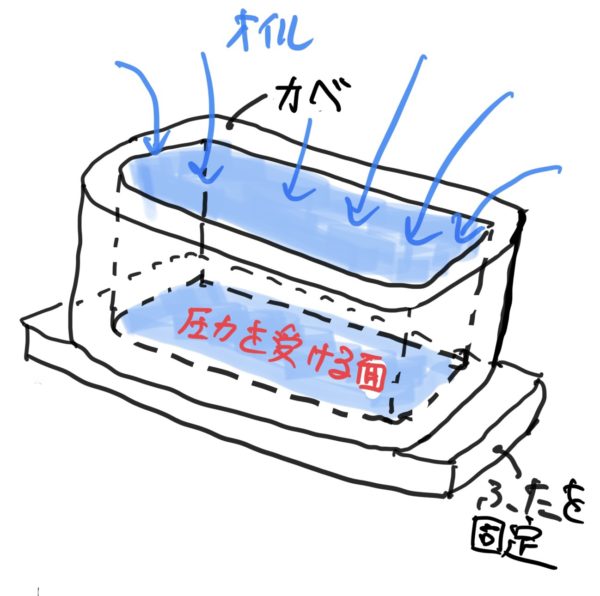
このような容器を圧力容器とか薄肉容器問題として扱うことが多い。別項でしっかり説明するつもりだ。
まとめ
実は紹介したはりは下の記事で解法を紹介している。
しかしながら実際の設計現場で一々計算していたらいくら時間があっても足りないので参考にして欲しい。
また実際には複数の複雑な荷重を受けることが多いのだが一つ一つを分解すると案外と紹介したような単純な荷重の組み合わせだったりする。
その時には以前に紹介した特異関数や重ね合わせ法を使えば楽に解ける。

ここまで説明しといてなんだが現実の設計現場ではミレーションで強度計算を行うことが多いので厳密解を関数電卓や手計算で求めることはかなり少ないと思う。
しかしレイアウト、スケッチ段階で無闇に何回もシミレーションを実施していたら時間が勿体無いしシミレーション担当の人に怒られてしまう。なるべくならば一回の計算で決めたいものだ。
そのためにはイメージが重要なので本講座でイメージできるように是非、挑戦して欲しい。
次回はようやく破壊の代表である座屈の解説をする。
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。






コメント