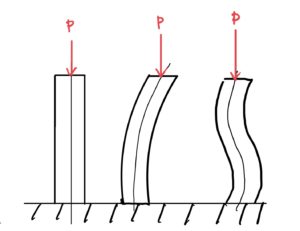
さて前回の説明で座屈というものがどういった変形なのかは理解できたと思う。
今回は、前回の座屈荷重をもとに座屈応力について説明する。
さらに座屈は全ての柱の長さで公式が適用できるわけではなく、場合によっては実験式を使用せざろう得ない時がある。
その実験式も紹介しよう。
また設計する上で座屈をさらっと検討するのに便利な係数があるので紹介する。これはとても重要だ。
では説明を始める。
様々な柱の座屈荷重
前回は単純な変形になる片側固定、片側自由の柱の座屈を説明した。
ここからは他のパターンの柱の座屈を紹介していこう。
両側自由端の座屈荷重
いつも通りまず例題を設定する。
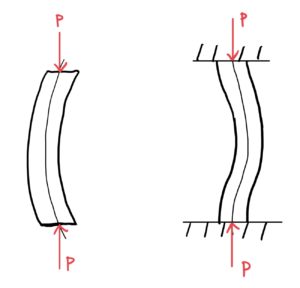
次の図のように長さlの断面2次モーメントI、弾性係数Eの両側自由端で荷重Pが両端部からかかる場合を考える。
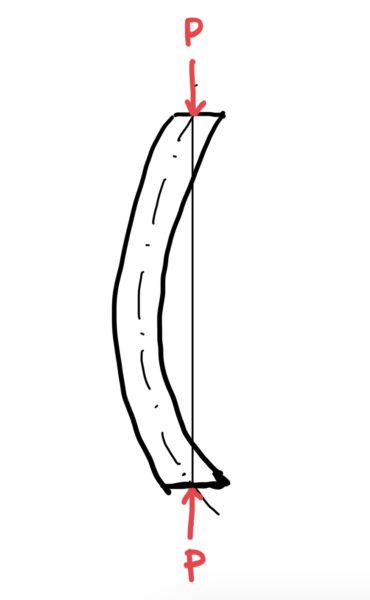
基本的な変形は図のようになりたわみの形を見ると真ん中でたわみ量yがMAXになるのでたわみ角θは真ん中で0になる。
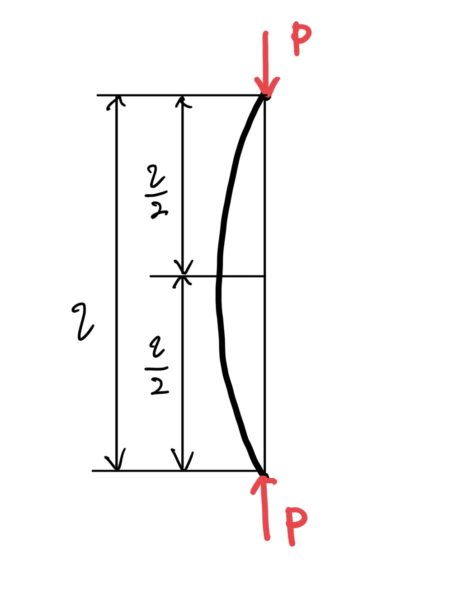
図を良く見ると長さが半分のところで前回で紹介した片側固定端、片側自由端と全く同じになるのがわかると思う。
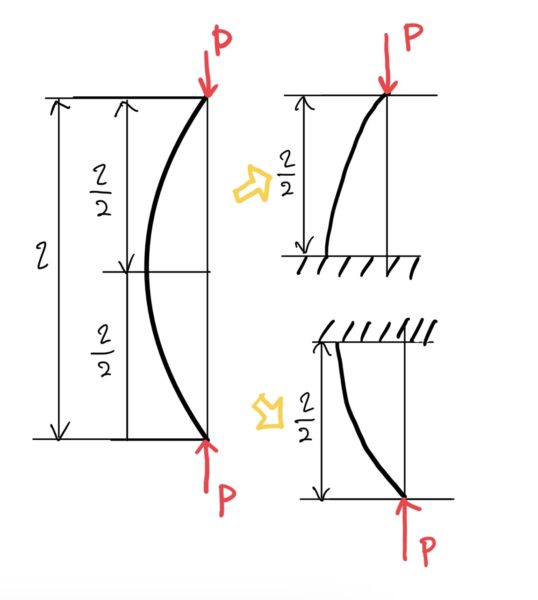
よって座屈荷重は前回で求めた座屈荷重$ Per=\frac{π^2EI}{4l^2} $のlの部分を$ \frac{l}{2} $にするだけで良いので次のようになる。
$ Per=\frac{π^2EI}{l^2} $(両側自由端)
これが両端自由端の座屈荷重になる。
両側固定端の座屈荷重
次に両側固定端の場合を考えてみよう。両側自由端と同じ設定で両側を固定する。
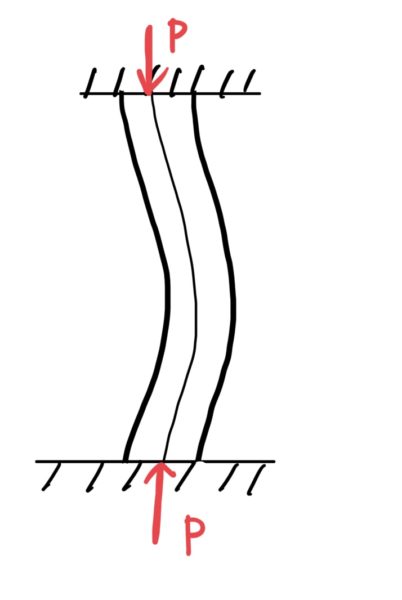
これもたわみの変形の形を良く見ると半分のところでたわみ量yがMAXになる。さらによく見るとたわみ角θは真ん中で0になりそれぞれl/4のところでMAXになる。
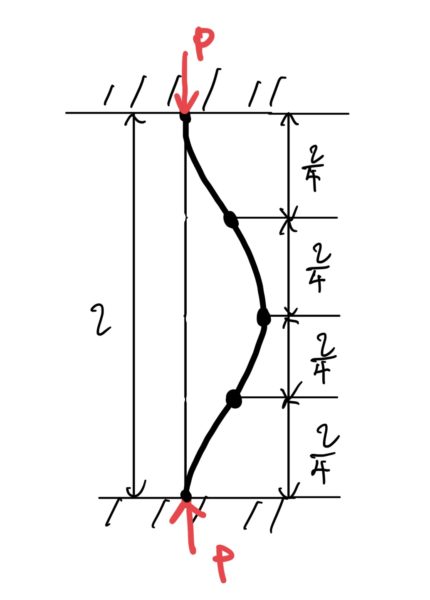
図を見ると片側固定端、片側自由端の柱がl/4で4個あるのがわかると思う。
よって座屈荷重$ Per=\frac{π^2EI}{4l^2} $のlの部分を$ \frac{l}{4} $にすれば良いので次の式になる。
$ Per=\frac{4π^2EI}{l^2} $(両側固定端)
これで両側固定端の座屈荷重がわかる。
座屈荷重の一般化
ここまでで多くの人が気付いているかとと思うが座屈荷重は係数を使って一般化できる。
係数をnとすると次の式で座屈荷重は表される。
$ Per=n\frac{π^2EI}{l^2} $
これをオイラーの公式と呼ぶ。
式をみてわかる通り柱が短いほど座屈荷重が大きくなる。なので長くするときは要注意だ。
このnの違いによって変形のモードは次のようになる。
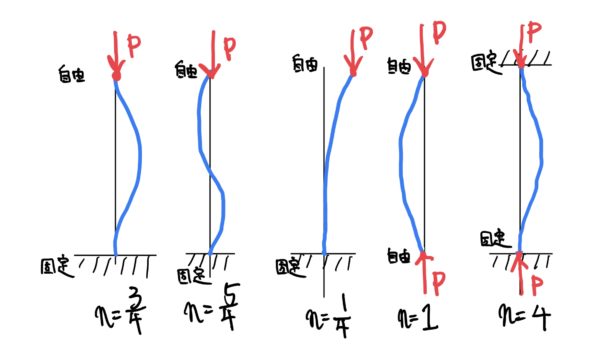
実際の設計では変形や条件を予想してnの値を決める。
また既存の構造を少し変える程度であれば以前のデータがあるはずなのでそこからnの値を引っ張ってくれば良い。
しかし全く新しい構造の場合は、実際に変形させないと本当の値はわからないので実験をすることを強く勧める。
座屈応力
求めた座屈荷重から座屈応力を考えてみる。
理想的な座屈においては荷重が座屈荷重を超えない限り柱は全く変形しないと考えるので座屈直前に柱に発生している圧縮応力を次のように表す。
$ σer=\frac{Per}{A} $(Aは断面の面積)
これを座屈応力と呼ぶ。
ここで座屈荷重Perにオイラーの公式を代入すると$ σer=nπ^2E\frac{I}{l^2A} $となる。
ここで$ k^2=I/A $とすると
$ σer=nπ^2E(\frac{k}{l})^2 $
ここでkの意味を考えていこう。
kの式を変形させると以下のような式にできる。
$ k^2A=I $
この式はどこかで見覚えがないかな?実は断面2次モーメントの定義”$ I=\int_{A}y^2dA $とかなり似ている。
かなり強引だがyとkを同じと見立てれば中立軸または図心からの距離と考える事ができる。
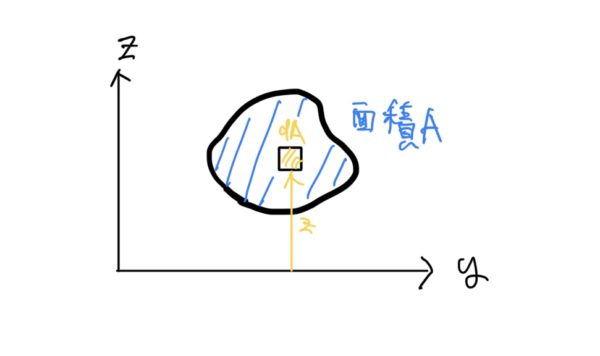
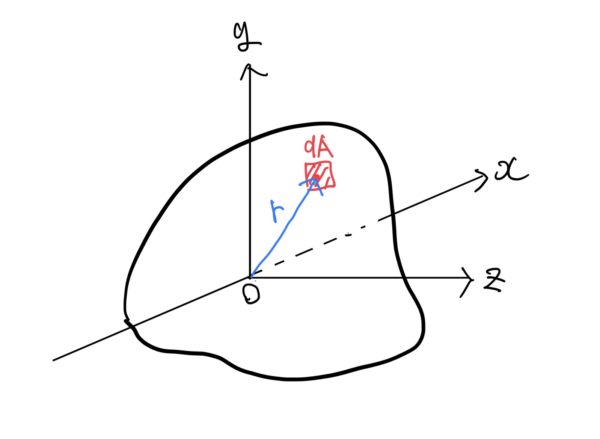
これらのことからkを断面2次モーメントの回転半径、断面2次半径、2次半径と呼ばれる。
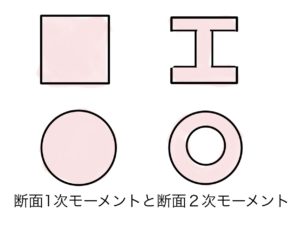
ここまで座屈、座屈荷重、座屈応力について材料が弾性限度域内であることを条件として考えてきた。
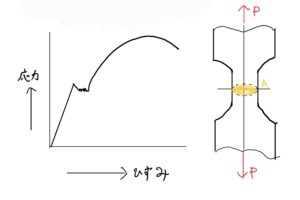
しかしながら柱が短いと座屈荷重を迎える前に座屈荷重、座屈応力が材料の弾性域を越えることがある。このような場合はオイラーの公式が適用できない。ちなみに座屈しないで降伏応力以上の荷重を与えると荷重面が陥没したりする。
そこで材料の降伏応力をσsとしてどのくらいの柱までオイラーの公式が適用できるかを次の式で確認することができる。
$ σs=nπ^2E(\frac{k}{l})^2 $
$ \frac{l}{k}=π\sqrt{\frac{nE}{σs}} $
これでオイラーの公式が適用できる範囲が材料の降伏応力、弾性係数と変形のモードで決まるのがわかると思う。
ここで$ \frac{l}{k} $を柱の細長比と呼ぶ。細長比が$ \frac{l}{k}>=π\sqrt{\frac{nE}{σs}} $でオイラーの公式が成り立つ。つまりlがそこそこ長くないと成り立たないことがわかる。
機械設計においては$ \frac{l}{k} $を設計において柱やリブ(高さL)の断面が円形状(直径D)に近い場合はL/Dとしそのままエルバイディーと呼ぶ(かなり強引)。
またかなり強引だが断面が円でない場合は断面積をAとしL/DをL/Aと考えて使うことがある。
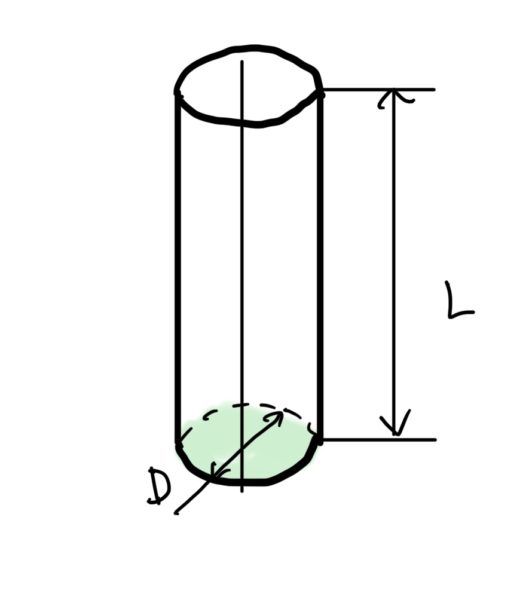
オイラーの公式の範囲内においてこのL/Dは値が大きくなればなるほど柱が長くなり座屈応力は下がって弱い構造になる。
このL/Dを比較することによって簡単に構造物の強度が比較できるようになる(絶対値はわからないが比較は重要)。
よって今まで使ったことがある実績のある構造物と設計対象のL/Dを比較すると強度の強弱が簡単に比較できる。
これは覚えておいて欲しい。
座屈応力の実験式
基本的に機械設計であればオイラーの公式でみておけば多くの場合で問題ない(建築、土木は知らない)。なぜならば構造物の大きさによるがL/Dがとんでもない大きさになることが少ない。
ただし場合によってはオイラーの公式が適用できない短い柱を使うことがあるのでその範囲で使える実験式を紹介する。ちなみに実験式なので式の意味を考えたり覚えたりする必要は一切ない。道具として存在と使い方がわかっていれば良い。
ここで鉄の定番材料である炭素鋼S30C,S35Cの長質(熱処理済み)を例にオイラーの公式が適用できない場合の座屈応力を考える。
主に実験式は3つジョンソンの式、テトマイヤーの式、ランキンの式である。
まずは詳細な説明に入る前に横軸を$ λ0=\frac{l}{k} $(細長比、L/D)で縦軸が座屈応力としたグラフを紹介する。
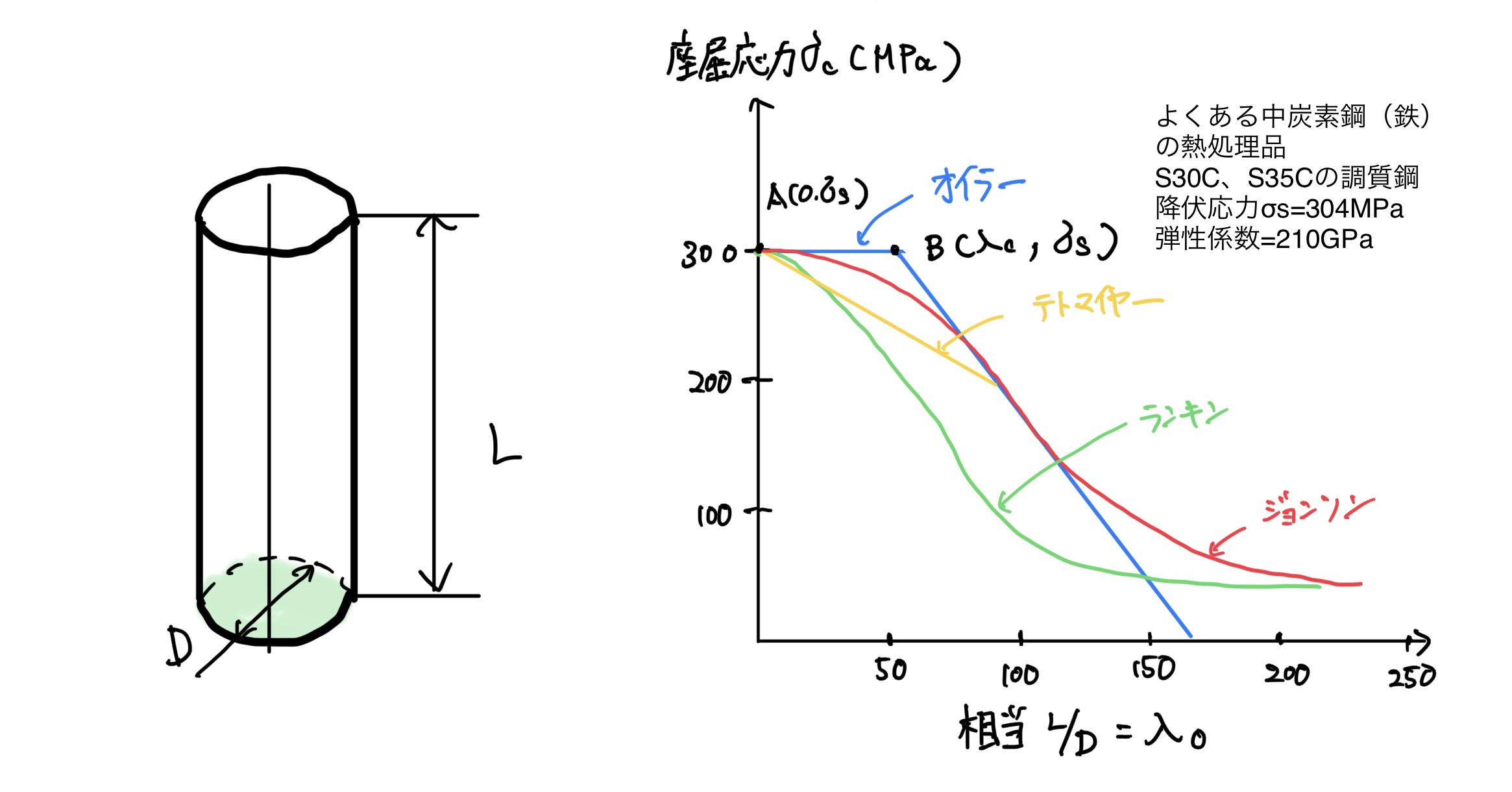
ランキンの式
3つの中で一番、重要なのがランキンの式だ(グラフの緑)。
これは柱が短いときに大きな荷重が入力される場合に使う。
グラフを見ればわかるがランキンの式が一番、小さな座屈応力を算出するのでこれで見ておけば強度だけに関しては、問題ない。
式自体は簡単で次のようになる。ランキンの式の座屈応力をσex、σsを降伏応力、σerをオイラーの公式の座屈応力λ0は細長比とする。
$ \frac{1}{σex}=\frac{1}{σs}+\frac{1}{σer} $
$ σex=\frac{σs}{1+σs\frac{λ0^2}{π^2E}} $
となるがこれも実際の座屈応力と合わないことが多くてランキンは次の式を提唱した。
$ σex=\frac{σ0}{1+a0(λ0)^2} $
ここでσ0は圧縮強さ(実験値)でa0は実験定数というなんとも言えない式だ。
ちなみに参考に変形のモードn=1(両端自由)のときは
・軟鋼(S30C,S35Cなど)でσ0が333MPa、a0が1/7500、λ0(細長比、L/D)が90未満
・硬鋼(SCM420,SCM435など)でσ0が481MPa、a0が1/5000、λ0(細長比、L/D)が85未満
・鋳鉄(FC200,FCD250など)でσ0が549MPa、a0が1/1600、λ0(細長比、L/D)が80未満
単純に硬くなれば硬くなるほど細長比、L/Dが小さい範囲でしか使えないということ。
いずれにせよ実験値なので既存の材料、構造ならばまともな会社ならばデータを持っているはずだし新材料、新構造の場合は実際にテストしてみるしかない(面倒ので新材や新構造を嫌う人も実際に存在する)。
後の金属材料などで説明するが自動車会社などの材料部門はこのような数値を出す仕事をしている。このような基礎データを持っている量も会社や組織の強さを示す重要なパラメーターになる。
ジョンソンの式
次はジョンソンの式を紹介するが筆者は実際に使用した記憶があまりない。しかし知識として知っておけば引き出しが増えるので是非、みておいて欲しい。
では式を紹介する。ここでは座屈強さの上限値を降伏点σsとして定義される。
$ σex=σs+C(λ0)^2 $(Cは定数)
ここで座屈応力σexのMAXが降伏点σs以下であることから上の式がオイラーの座屈応力σerに接するように設定すると
$ C=-\frac{σs^2}{4π^2E} $
となりσexは次のようになる。
$ σex=σs-\frac{σs^2(λ0)^2}{4π^2E} $
適用できる範囲は$ \frac{σs}{2} $<σex<σsである。
これは割と精度が良いらしい。
テトマイヤーの式
テトマイヤーの式は軟鋼(S30Cなど)によく合う式である。言い換えれば応力ー歪み線図の弾性域がなだらかな材料によく合う。
式を紹介する。
$ σex=σ0(1-a0λ0) $(σ0、a0はともに実験値)
でとっても簡単で変形モード n=1の場合はσ0が304MPaくらい、a0が0.00368くらいでλ0は105未満で使える。
基本的に柔らかくて粘りがある材料でよく合う(真鍮とか)。
これで実験式の紹介は終わる。
まとめ
では座屈をまとめていく。
・座屈荷重は、$ Per=n\frac{π^2EI}{l^2} $で求められこれをオイラーの公式という。
・座屈荷重は柱が短いほど高く、長くなると低くなり柱は弱くなる。
・座屈応力は、$ σer=\frac{Per}{A} $(Aは断面の面積)で求められる。ただし前提として座屈応力が材料の降伏点以下の場合のみに使える。
・オイラーの公式の適用範囲は、細長比$ λ0=\frac{l}{k}≒L/Dとk^2=\frac{I}{A}$で判定ができる。
・オイラーの公式が使えない場合は実験式を使う。実験式の中でランキンの式が最も小さな座屈応力を算出する。
・L/Dは座屈強度を比較する上でとても大切な指標になる。
・新材料、新構造で正確な座屈応力を知るにはテストをするしかない場合もある。
となる。
ここまでで基本的な構造物の応力、歪み、変形は一通り終えた。
次回からは本格的に破壊について考えていくがその前に応力集中について少し説明する。
破壊が終われば材料力学の基本的な部分が終わるのでもう少し頑張って欲しい。
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。






コメント