今回から新シリーズの初心者でもわかる材料力学を開始する(今までシリーズだったのか?)。
まず最初に材料力学の基本中の基本である応力の説明をする。
“もう解ってるよ“という人も多いと思うが今後、解説していきたい機械要素設計(ネジ、ギヤ、ピン、リンク機構など)を説明するのにどうしても避けて通れないのでおさらいの意味を兼ねて説明する。
また今回は決まり事の説明が多く、実践でのコツとかがあまり記載できないが我慢して欲しい。
応力の定義
まず筆者も数十年前にこんがらがったのだが応力と力の違いから説明していく。
定義としては、次のようになる。
・F(力または荷重)は、物体が外から受ける力や荷重のこと(英語で力はFORCE,荷重はLOAD)
・σ(応力)は、物体内部に働く力のこと(英語で応力はSTRESS)
これは機械の強度計算を行うときに非常に大切なことなので是非、覚えておこう。
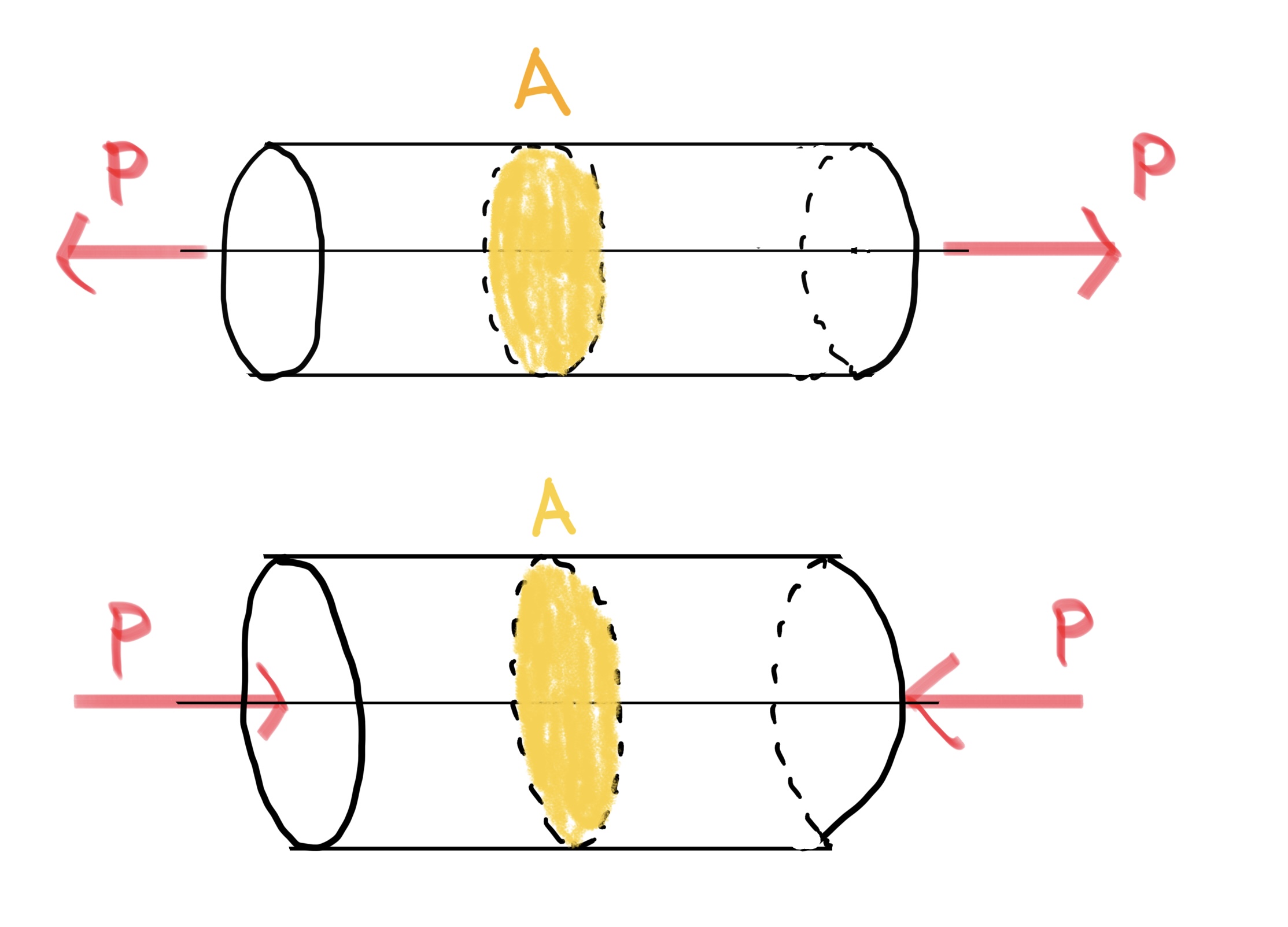
実際に図で説明すると(円柱を例にとる)
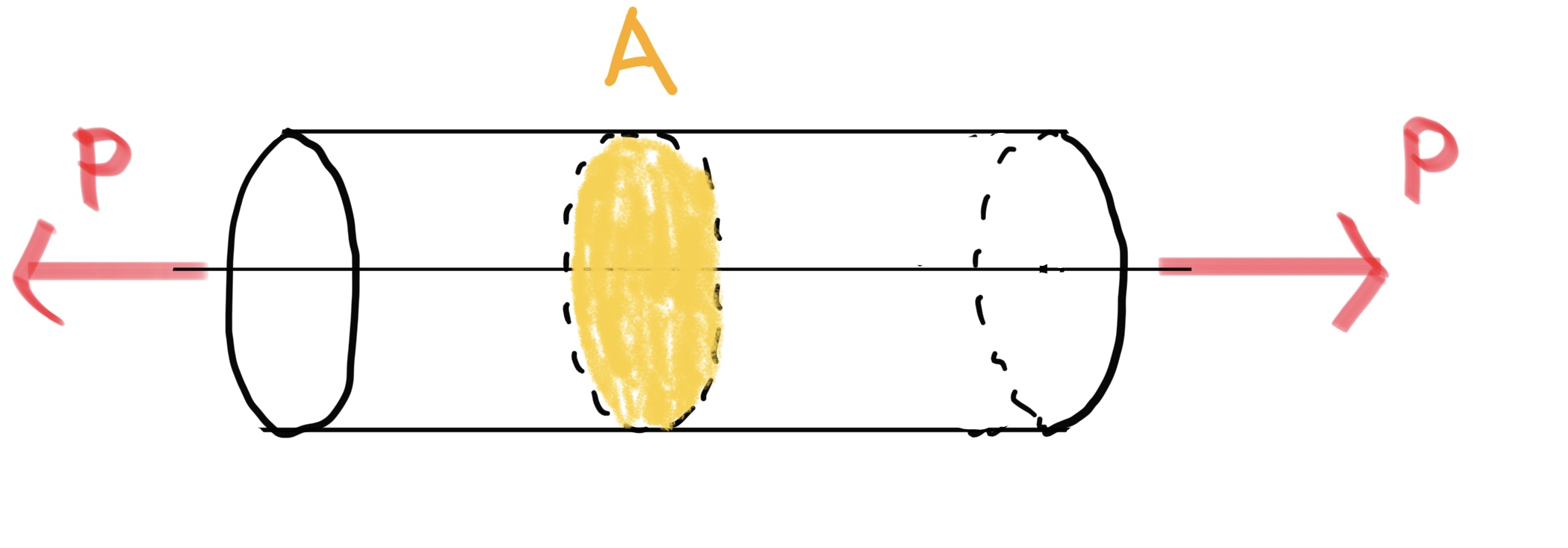
ここではPが外から受ける力になり物体の断面Aに発生する応力σは、次の式で表される。
$ σ(応力) =\frac{P(外力)}{A(面積)} $
これが応力の定義で力または荷重Pを面積Aで割った値だ。
大切なのは単位で外力Pはニュートン(N),面積Aは平方メートル($ m^2 $),応力σの単位はパスカル(Pa)だ。
ここでちょっとしたコツなのだが設計で使う単位はほとんどがmmである。
Paの単位は$ \frac{N}{m^2} $なので一見すると扱いにくい。
しかし面積は、$ mm^2 $なのでmに直すと$10^-6mm $になる。
これを分母にしてもう一度Paを見ると$ \frac{10^6N}{m^2} $になる。
この単位を書き直すとメガパスカルMPaとなり分かり易くなる。
だから力Nを面積 $ mm^2 $で割ったら数字がそのままでメガパスカル MPaになると覚えていると便利だ。
ちなみに$ 10^3 $がキロ Kで$ 10^6 $がメガ Mで$ 10^9 $がギガ Gである。
パソコンとかと一緒なので是非、覚えておこう。
応力の種類
応力の定義がわかったところで、次に応力の種類について説明していく。
まず始めに引張り応力を説明する。(円柱を例とする)

$ 断面Aの引張り応力σ=\frac{P(外力)}{A(面積)} $ 単位はパスカル(Pa)で符合は+である
ここで大切なのが符合である。
引張りが+は絶対に覚えておこう。
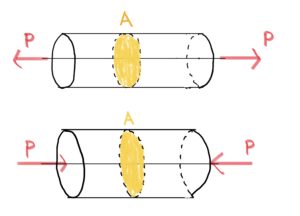
圧縮応力を説明する。(円柱を例とする)
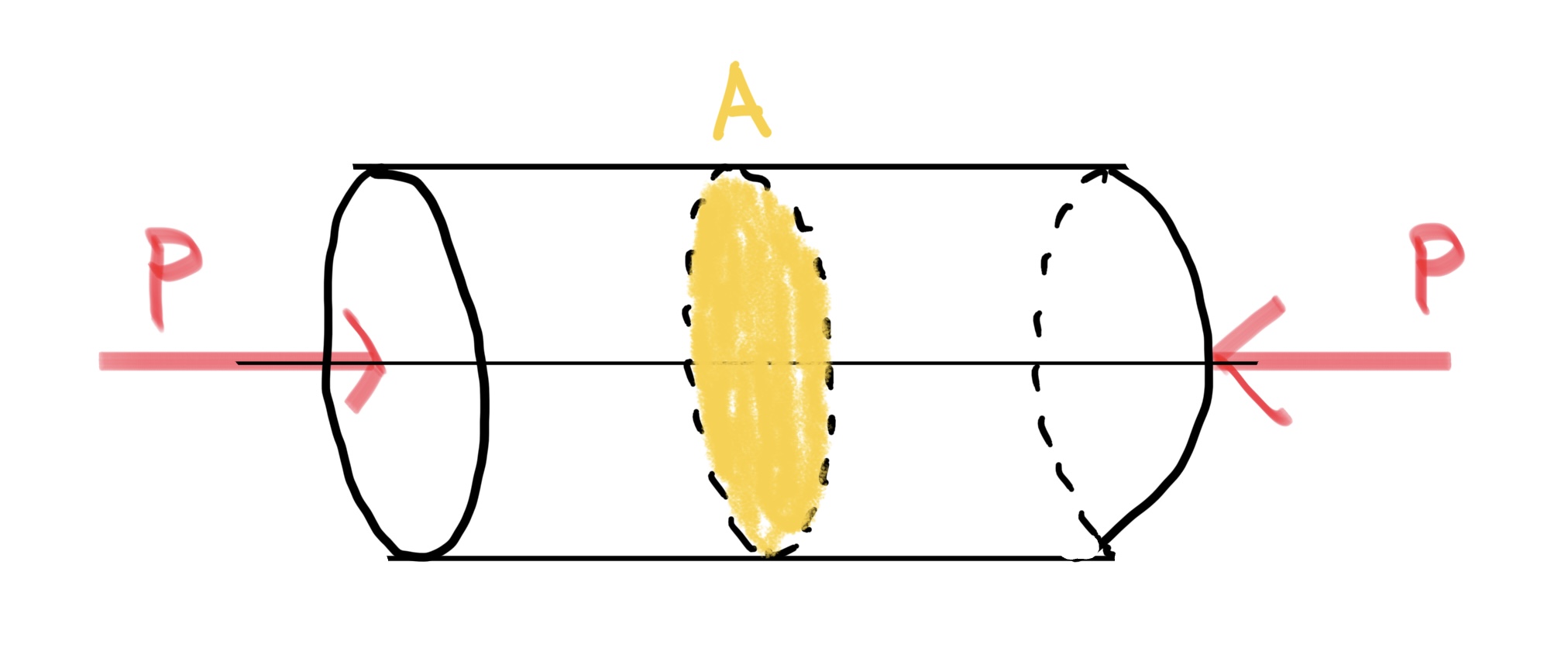
$ 断面Aの圧縮応力σ=\frac{P(外力)}{A(面積)} $単位はパスカル(Pa)で符合は−である。
ここで符合の大切さがわかってもらえると思うが
・圧縮の符号は−は絶対に覚えておこう。
後に説明するが引張りと圧縮では材料の破損形態が全く異なっており、許容できる応力も全く異なるので引張りか圧縮の区別がわかることが非常に大切なのである。
・引張が+、圧縮がーは絶対に覚えておこう。
次に応力の基本である剪断応力(せんだん)を説明する。
今度の例は板2枚に円柱状のピンが入っていて板を引張る状態を想像して欲しい。
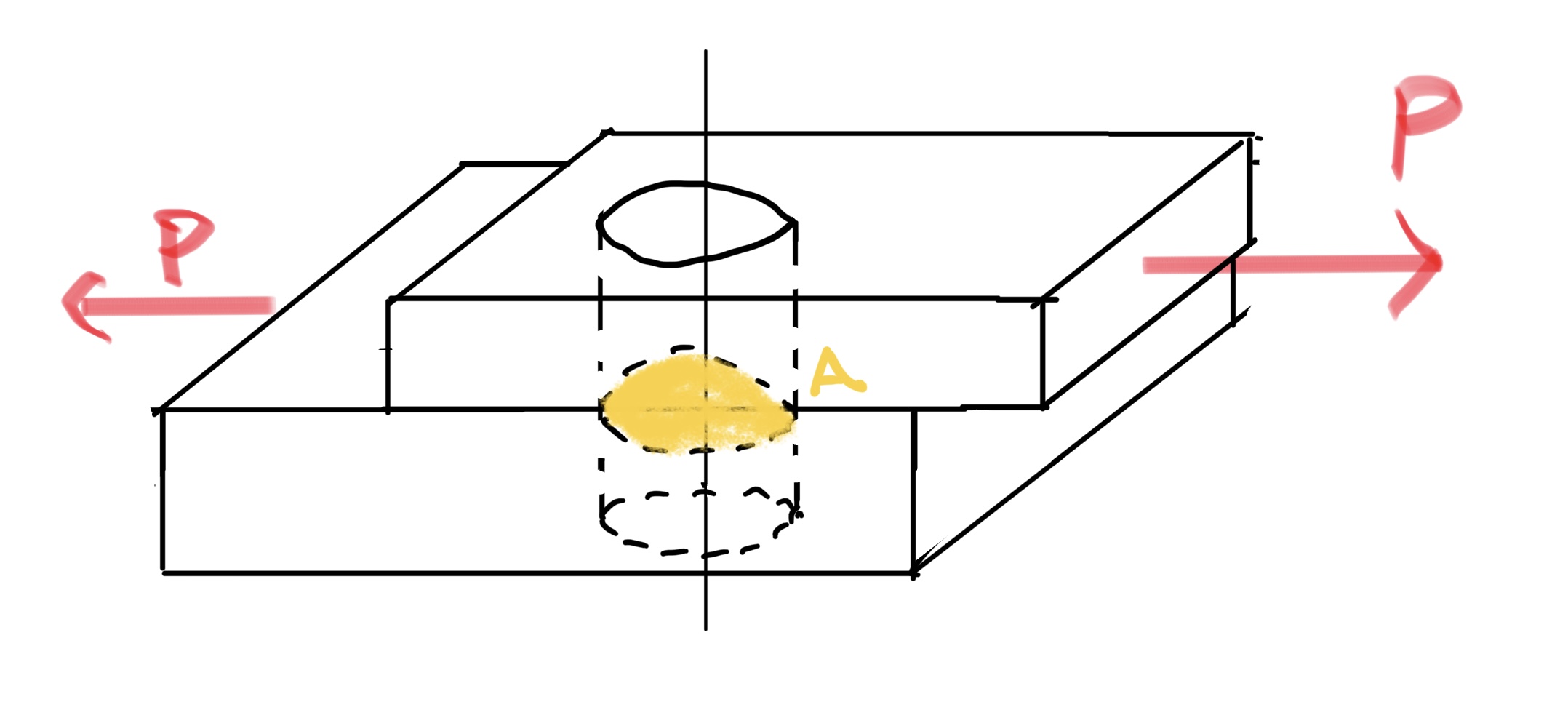
このままではわかりにくいのでピンを抜き出すと
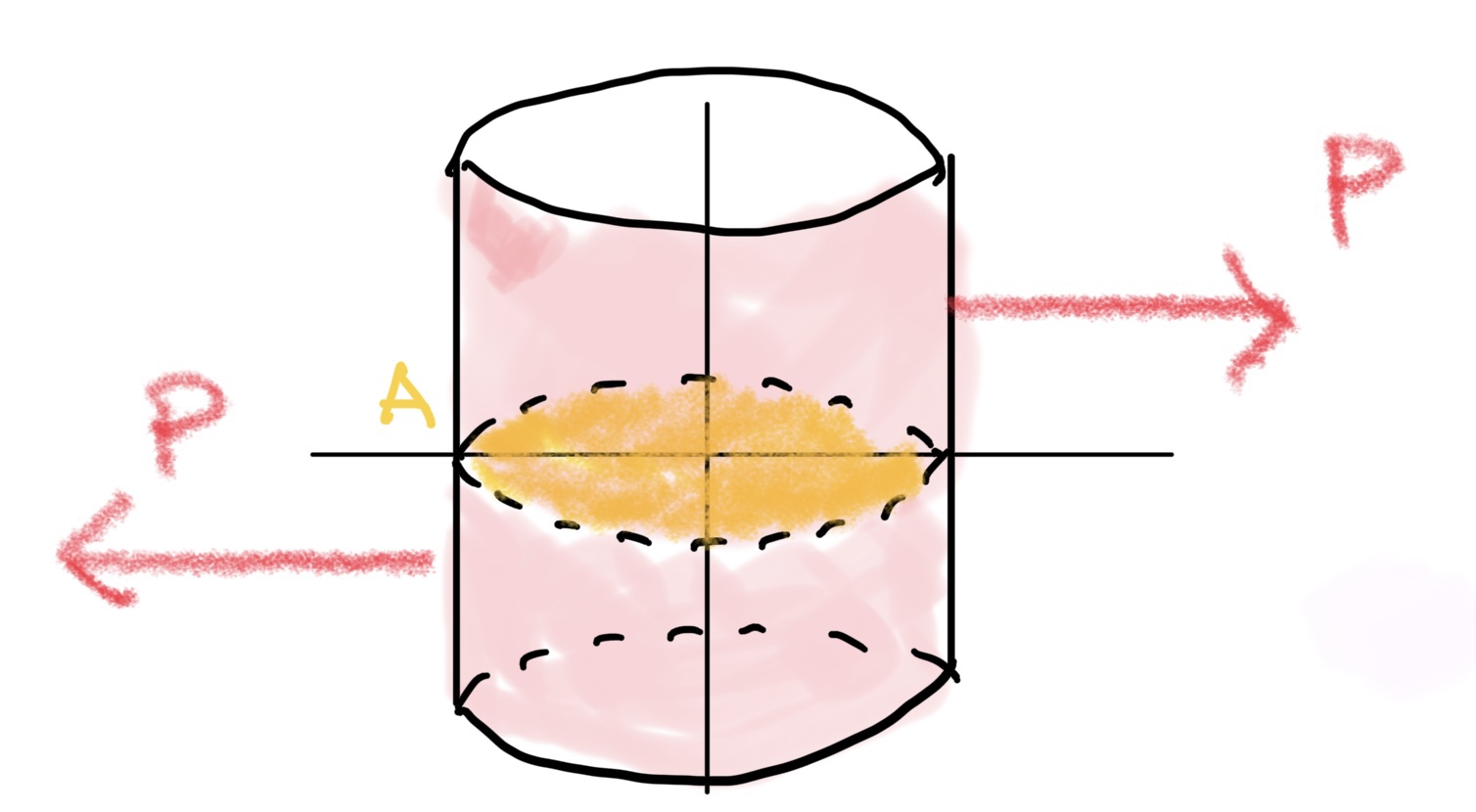
左右に引っ張られるピンを想像して
$ 断面Aの剪断応力τ=\frac{P(外力)}{A(面積)} $単位はパスカルPaであり符合は、+である。
剪断応力(せんだん)はτ(タウ)で表されて符合は+である。
筆者の経験不足かもしれないが剪断応力で−は見たことがない(はりの剪断力は別)。
あとは、捻り応力があるが少し難しいので後に解説する。
これで応力の種類は全てである。
次に材料力学で大切な概念があるので説明する。
歪み(ひずみ)
歪みについて説明していく。
これはメチャクチャ大切な概念なのである。
ではまた、円柱を例にするとまず外力Pが円柱に発生し応力σが発生する。

応力が発生すると物体は変形する。
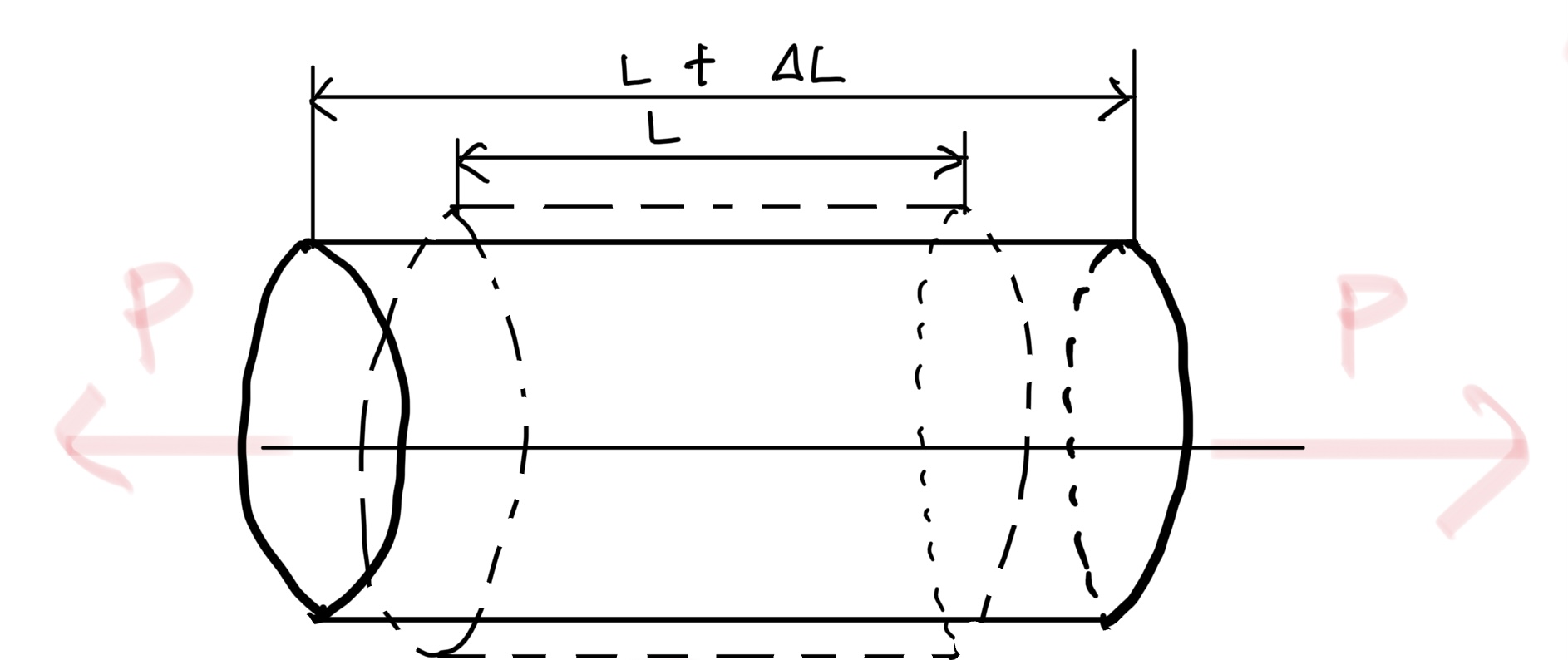
当然、引っ張れば物体は伸びるのだ。
ここで歪みの定義をする。
$ 歪みε=\frac{L+ΔL}{L} $単位は無い(無次元量)
歪みはε(イプシロン)で表され延びた長さ(L+ΔL) (Δデルタ)を元の長さLで割るだけ。
後々にメチャクチャ大切なので覚えておこう。
また単位も重要でしつこいが引張りが+で圧縮が−である。
次に少し複雑なのだが剪断歪みについて説明しよう。
またお馴染みの図で考えると

ピンを取り出すと

変形を考えると(ピンを正面から見てみると)
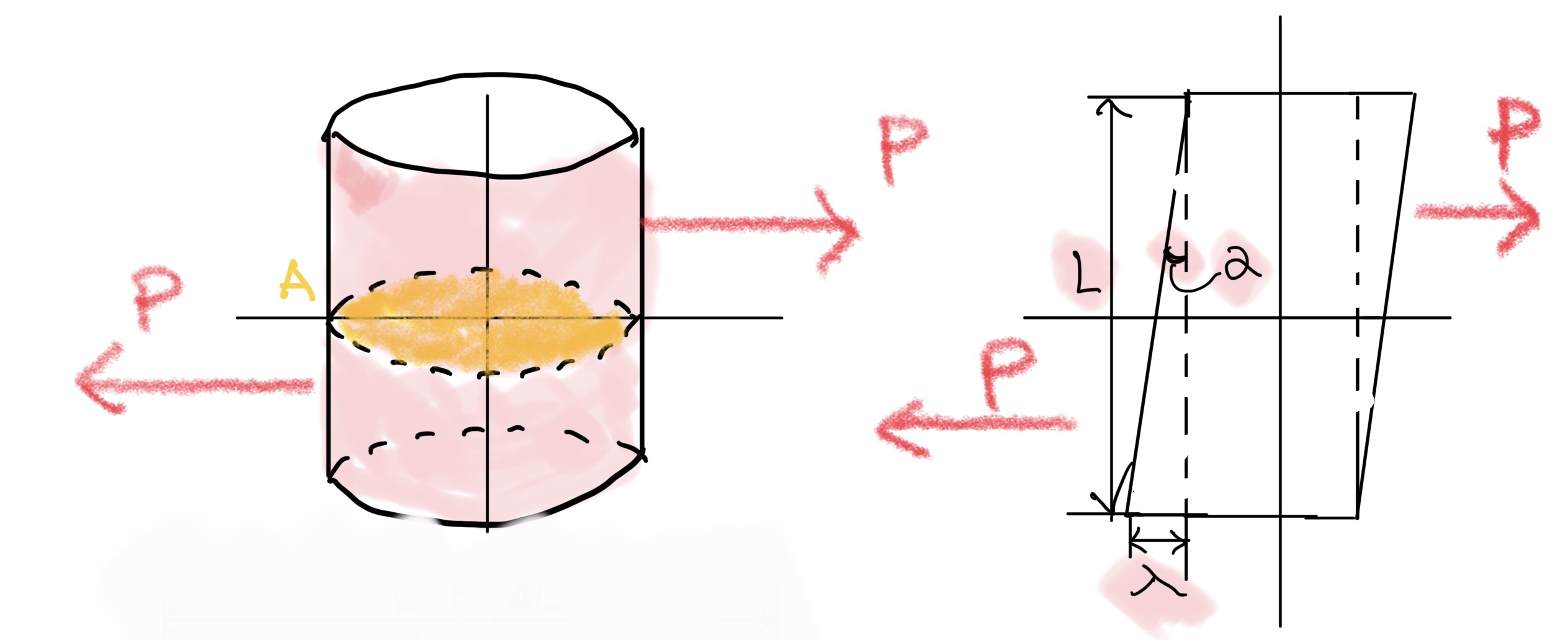
そう平行四辺形みたいな形になる。ここで剪断歪みを定義すると
$ 剪断歪みγ=\frac{λ(変形量)}{L(元の長さ)}=tan α(角度) $単位は無い(無次元量)符合が+
剪断歪みはγ(ガンマ)で表され変形量λ(ラムダ)を元の長さLで割る。符合は+。
筆者の経験不足か−は見たことがない。
これで歪みが定義できた。
この歪みを使って材料のメチャクチャ大切な物性値(特性)があるのでそれを説明する。
また再び、円柱が引っ張られた状態を考えよう。

引っ張ると物体は伸びる

お気づきかと思うが物体を引っ張ると伸びるだけでなく径方向に縮むのだ。
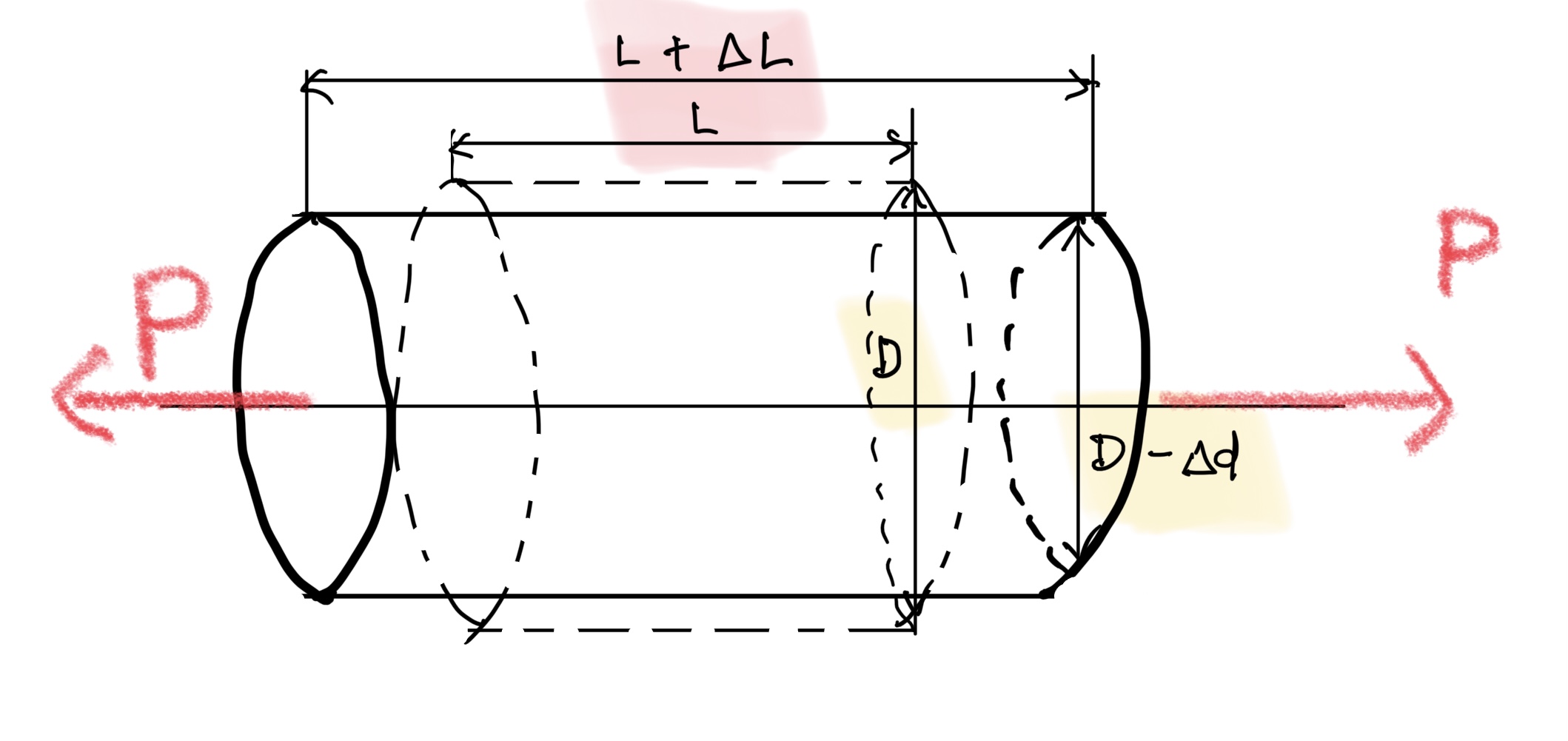
ここで伸び方向を縦歪み、縮む方向を横歪みとする。
定義で荷重方向を縦、荷重方向に対して直角方向を横とするルールがある。
ここで前の式から縦歪みεは$ \frac{L+ΔL}{L} $,横歪みε‘は$ \frac{D−Δd}{D} $になるのがわかると思う。
これで大切な値が定義される。
$ ポアソン比ν=\frac{|ε’|(横歪み)}{|ε|(縦歪み)}=\frac{1}{m} $
ポアソン比ν(ニュー)は物体にある外力を加えた時の横歪みε’を縦歪みεで割った値である。ポアソン比を$ \frac{1}{m} $と表した場合にmをポアソン数と呼ぶ
ちなみに式中の|記号|は絶対値とよび中の値から符合を取り去った値のこと表す(絶対値)。
このポアソン比がメチャクチャ大切で機械設計で言うと圧入とかギヤとかありとあらゆる機械要素の強度計算で使うので是非、覚えておこう。
まとめ
慣れないと覚えるのが大変だと思うが基本的なルールになるので是非、覚えて欲しい。
また機械設計者は学者ではないので必ずしも覚えなくていいがどこに書いてあるのか?何を調べればわかるのかが?できれば良いと思う。
つまり正しい検索能力を身につけるのが重要なのだ。
最後に繰り返すが大切なポイントは、
・外部から働く力は力や荷重(外力)、荷重で物体内部に働く力が応力である。キチッと分けよう。
・応力、歪みの符合が+の時は引張りで−の時は圧縮である。
・歪みとは、伸びた全長さ(L+ΔL)を元の長さ(L)で割る無次元量を示す(単位がない)。
・物質は、引っ張ると縦に伸びて横に縮む変形をする。
・縦と横の歪みの比の逆数であるポアソン比は、物性値で大切なことである。
筆者は学生時代に+と−の違いを単なる座標上の向きの違いくらいにしか捉えてなかったのでメチャクチャ苦労した(始めからつまづいてしまった)。
力学においては、符合は大切な意味がある場合が多いので気をつけよう。
次回の初心者でもわかる材料力学は、弾性と応力-歪み線図について説明する。
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。





コメント