今回は断面二次モーメントの実際の求め方を説明していく。
実際の設計現場で断面二次モーメントはCADがあればコマンドで簡単に求められる。
しかし新たな構造物を設計するときに検討段階で思いついた形状を全てCADで正確な断面図を作成したり3Dモデルをつくって求めていたら時間がいくらあっても足りない。
だからこそ“この断面なら断面二次モーメントはおおよそでこのくらい“とイメージが持てることが大切である。
少なくとも外力を受ける方向に対して断面二次モーメントが高いのか低いのかくらいは瞬時にイメージが沸くことが望ましい。
まず断面二次モーメントの前に断面一次モーメントの簡単な数学的な特性を説明する。
断面一次モーメントの性質
まずは断面一次モーメントの定義を思い出そう。Aは面積。
$ 断面一次モーメント=\int_{A}ydA $
ここで前回で説明した特性ではりの中心を原点とすると断面1次モーメントは0になる(断面の曲げ応力の総和は0)。
$ 断面一次モーメント= \int_{A}ydA=0 $
この特性を数学的に見ていこう。
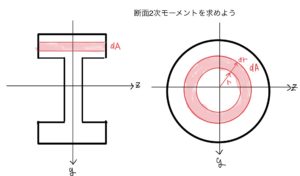
断面が四角で座標原点をはりの中心Gとすると断面1次モーメントの計算イメージは下の図のようになる。
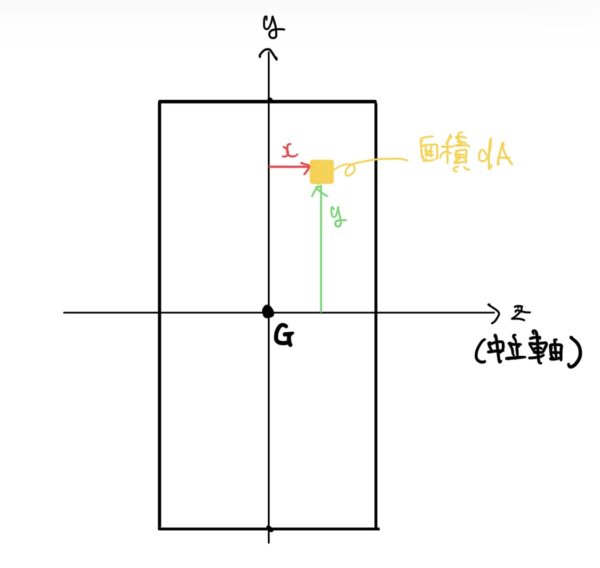
ここで四角形は原点Gを中心に上下左右対象なので面積で積分する断面1次モーメントは0になる。
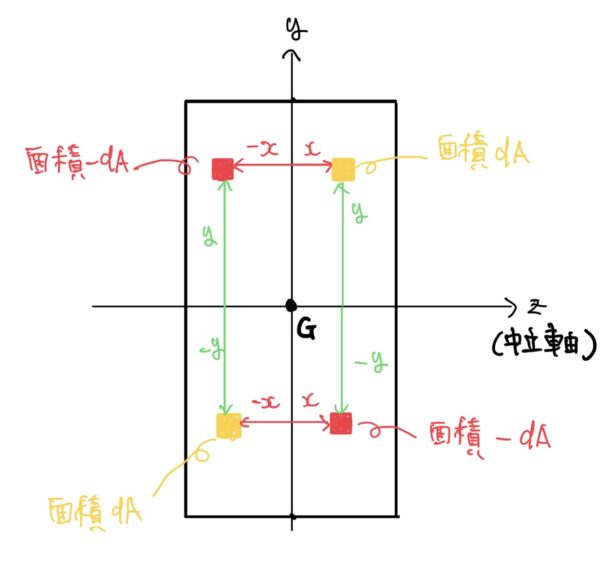
実際に断面1次モーメントを計算すると下の図のようにzy平面と-z-y平面の面積がdA、z-y平面と-zy平面が-dAでお互いに打ち消しあって0になる。
このように断面1次モーメントが0になる原点座標のことを図心と呼ぶ(図心、中立軸、中立面は重要)。
つまり図心Gを原点とした断面一次モーメントは0になる。
このように図心がわかる場合は断面1次モーメントは定義より0とわかるのだが図心がわからない場合を考えてみよう。
図心を通らない適当な座標を原点としての断面1次モーメントを考えてみよう。適当な座標の原点をOとして新たな座標系を(x1、y1)とする。
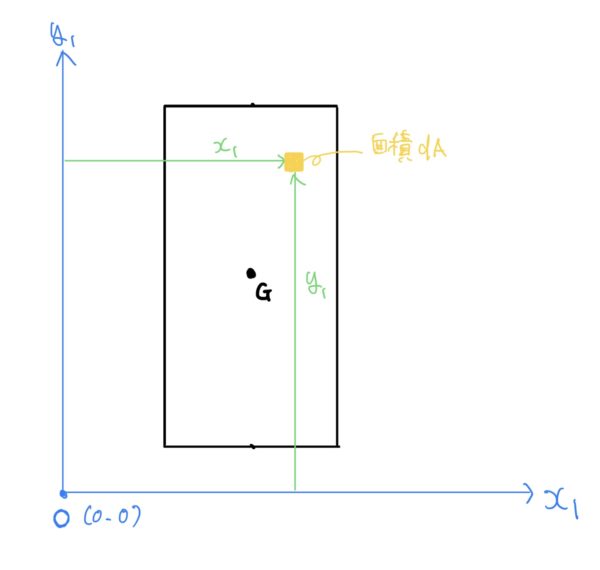
上の図の座標系に図心を仮でG(yG、xG)とし座標系(x、y)を置いてみよう。
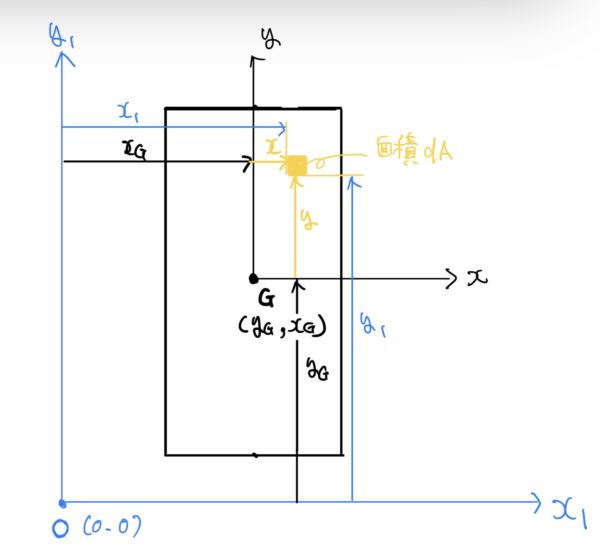
このときに図心の座標系(x、y)は次のように表せる。
$ x=x1-zG $
$ y=y1-yG $
図心の座標系(x、y)の断面1次モーメントに代入する。
$ \int_{A}x=\int_{A}x1dA-\int_{A}xG dA$
$ \int_{A}ydA=\int_{A}y1dA-\int_{A}yGdA $
図心の座標系の断面1次モーメントは0、座標系(x1、y1)での図心周りの$ \int_{a}yGdA $はyGA(Aは四角の面積)なので
$ 0=\int_{A}x1dA-xGA $
$xG=\frac{\int_{A}x1dA}{A} $
$ 0=\int_{A}y1dA-yGA $
$ yG=\frac{\int_{A}y1dA}{A} $
となり図心の座標は断面一次モーメントを面積で割ると求まる。つまり図心がわからない場合は適当な座標系の断面1次モーメントと面積が分かれば求められるのだ。
逆に図心が分かれば適当な座標系の断面1次モーメントが簡単に求められる。
$ \int_{A}x1=xGA、\int_{A}y1=yGA $
後に機械力学で説明するが物体の重心の面積バージョンだと思ってもらって良い。
物体における重心が断面の面積における図心である。
次は断面二次モーメントの求め方を紹介しよう。
断面二次モーメントを求める
まずは断面二次モーメントのおさらいをしよう。
定義では
$ y軸方向の断面2次モーメントIy=\int_{A}z^2dA $
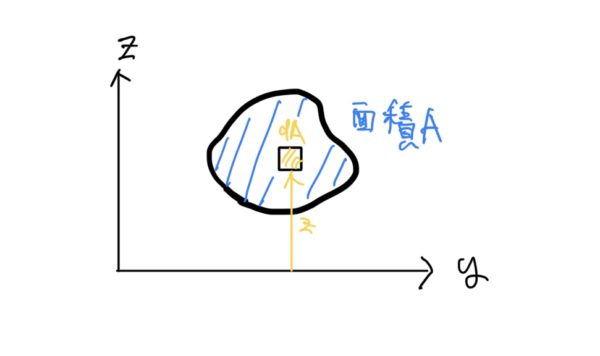
ここで面積の積分なんてどうやんの?と思われるがやり方がちゃんとある。
ではいくつか実際に断面二次モーメントを求めてみよう。
四角い断面の断面二次モーメントを求める
まずは断面が四角の場合を求める。
例として横幅がbで高さがh(半分で$ \frac{h}{2} $)で座標原点を図心とした断面でz軸方向の断面二次モーメントを考えよう。
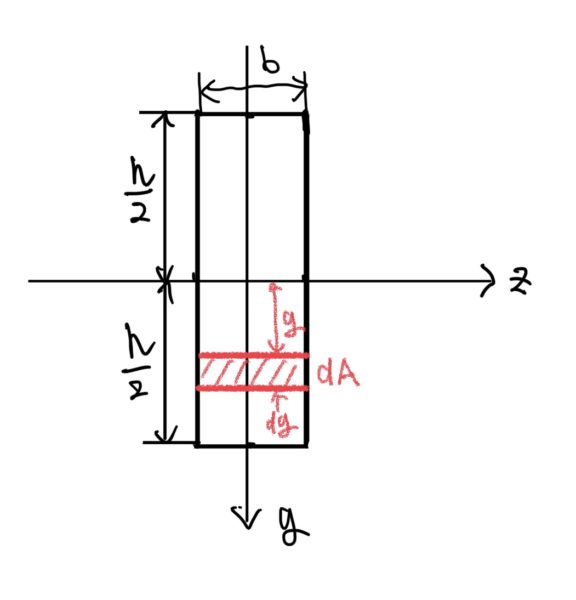
ここでポイントだ。求める軸方向の直角方向を変数として面積を定義するのだ。
この例題で求めたい軸方向はZ軸なので変数になるのはy軸、y軸を使って面積を表すと幅がbだからbyになる。だから積分する微小断面積dAは下の式で表せる。
$ dA=b×dy $
なのでこれを断面二次モーメントの式に当てはめると
$ Iz=\int_{A}y^2dA=b\int_\frac{-h}{2}^\frac{h}{2}y^2dy $
となり、これを解けば
$ Iz=\frac{bh^3}{12} $
となる。
ここでポイントなのがy軸方向に肉厚があると3乗で断面二次モーメントが増える。
3乗で断面2次モーメントが増加するのではりの断面内に発生する曲げ応力が激減するのだ(前回の内容になるが曲げ応力は$ σ1=-\frac{M}{Iz}h1、σ2=\frac{M}{Iz}h2 $)。
I形断面の断面二次モーメントを求める
次はI形断面で考えてみよう。
例題の設定は図の通りでZ軸周りの断面2次モーメントIzを求めよう。
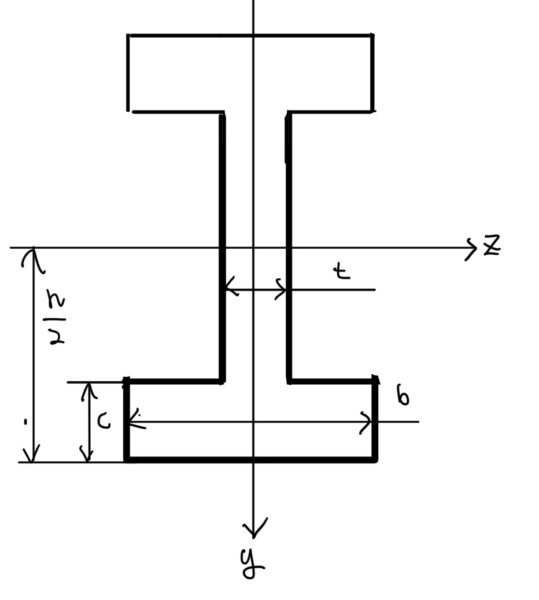
上の例題とは異なって途中で断面の幅が変化しているので少し工夫が必要になる。
断面を見ると2種類の断面があるのでそれぞれを分けて考える。
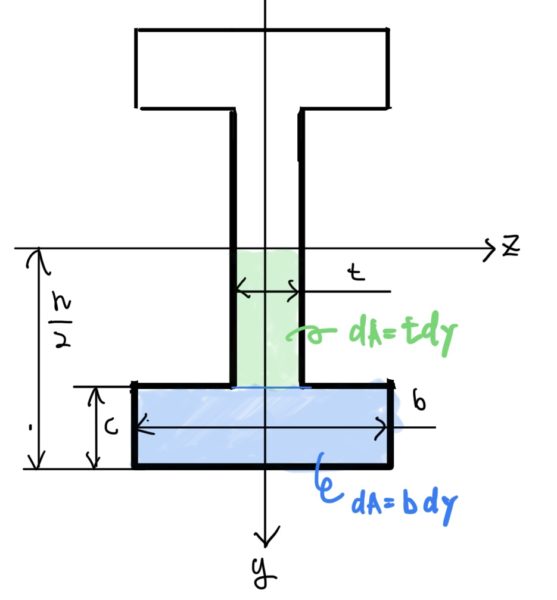
後はそれぞれのy軸方向での微小面積を定義して断面二次モーメントを求める。またここでz軸を基準に対称な形状なので半分だけ求めて後で2倍すれば良い。
y軸方向の+側の微小区間に置いて図心Gの断面積、図心G1の断面積は次の式で求められる。
$ G1の断面積=tdy(0≦y≦\frac{h}{2}-c) $
$ G2の断面積=bdy(\frac{h}{2}-c≦y≦\frac{h}{2}) $
これを断面二次モーメントの定義に当てはめると
$ Iz=\int_{A}y^2dA=2t\int_{0}^{\frac{h}{2}-c} y^2dy+2b\int_{\frac{h}{2}-c}^{\frac{h}{2}} y^2dy $
計算すると
$ Iz=\frac{bh^3}{12}-\frac{(b-t)(h-2c)^3}{12} $
となる。
このようなI型断面でものやはりy軸方向hが3乗で断面二次モーメントが増えるのでなることを認識しておこう。
断面二次極モーメント
ここまでは微小面積を求める際にZ軸方向の値は定数(bとかt)だったので計算が楽だったがZ軸方向も変化する場合は式が複雑になって計算がかなり面倒になる。そこで断面2次モーメントが持つ特性を活かして楽をする方法を考えていく。
その新たな特性は断面二次極モーメントと呼ばれているものだ。全然、難しくはない、むしろ簡単だ。
今まである梁のある断面を切り取って2軸の座標Z、Yで考えていたが座標Z、Yに直角なx軸を足して軸周りの距離rで考えてみるだけである。
数学がわかる人ならば単純にデカルト座標から極座標に変えてみたというだけである。
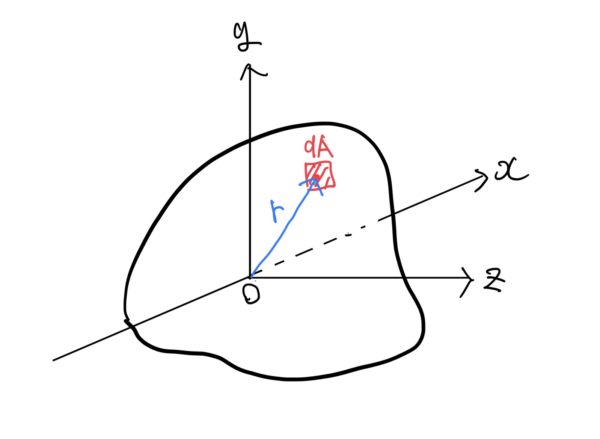
ここでx軸に関する断面二次モーメントIpを考えると
$ Ip=\int_{A}r^2dA $
となり、これを断面二次極モーメントと呼ぶ。
しかも$ r^2=y^2+z^2(rをベクトルと考える) $なので上の式に代入すると
$ Ip=Iy(y軸に関する断面二次モーメント)+Iz(z軸に関する断面二次モーメント) $
つまり任意の断面の直行する軸同士の断面二次モーメントを足せば断面二次極モーメントが求まる。
この性質を使うと丸軸の断面二次モーメントが簡単に求まる。
丸棒の断面二次モーメント
では例題を設定しよう。
直径dの丸棒の断面の図心を原点としてZ、Y、X軸を設定する。
ここで断面二次極モーメントを考えてみよう。
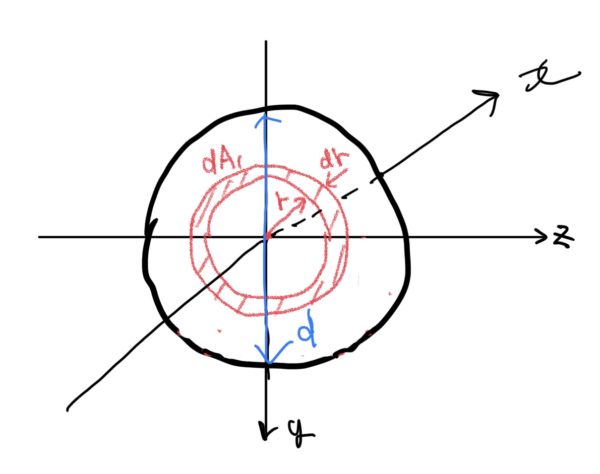
図より原点から距離rでの微小円の面積を定義すると(円の周長×幅)
$ dA=2πrdr $
から断面二次極モーメントの定義に代入すると
$ Ip=\int_{A}r^2dA=2π\int_{0}^{\frac{d}{2}}r^3dr=\frac{πd^4}{32} $
ここで断面の対称性から$ Iy=Iz $であるので
$ Iz=\frac{Ip}{2}=\frac{πd^4}{64} $
となる。
ここで重要なのは丸棒の場合、直径の4乗で断面二次モーメントが増加することである。
つまり直径を大きくすれば曲げ応力がかなり下がるのだ(前回の内容になるが曲げ応力は$ σ1=-\frac{M}{Iz}r1、σ2=\frac{M}{Iz}r1 $)。
また中空にしても断面二次モーメントはそんなに下がらない。
例えば外径をd1、内径をd2とした中空軸の断面二次モーメントは
$ Iz=\frac{πd1^4}{32}-\frac{πd2^4}{64} $
で$ d2^4≪d1^4 $なので多少の肉抜きではビクともしない。
丸棒のねじりでもそうだが曲げにも丸棒断面は直径に大きく依存し中空にしても発生する応力はほとんど変化しないのだ。
つまり軸はコストが許せば中空にした方が軽くて、そこそこ丈夫な構造物になる。
次が最後で断面二次モーメントの数学的な特性を説明する。
平行軸の定理
平行軸の定理を説明するのに例題を設定しよう。
ある断面の図心Gを中心とした座標と図心Gを通るz軸に平行で距離eだけ離れた軸z’が存在する。断面の面積はAとする。
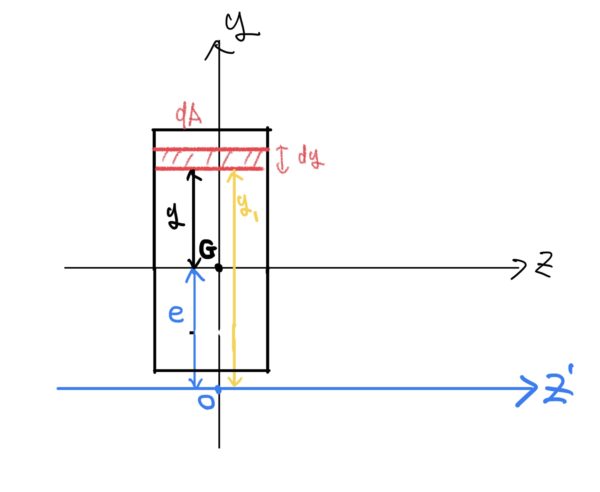
ここで軸z’に関する断面二次モーメントIz’を求めてみよう。
$ Iz’=\int_{A}y^2dA=\int_{A}(y+e)^2dA=\int_{A}y^2dA+2e\int_{A}ydA+e^2\int_{A}dA $
ここで展開した$ \int_{A}y^2dA $はz軸に関する断面二次モーメント、$ \int_{A}ydA $は図心の断面一次モーメントで0になり残った$ \int_{A}dA $はただの面積になるので次のようになる。
$ Iz’=Iz1+e^2A $
これを平行軸の定理と呼ぶ。
まあ、簡単に言えばある距離eだけ離れた平行な軸での断面二次モーメントはもとに対して$ e^2A $だけ足せば良い。
ちなみに機械力学で説明するが慣性モーメントも全く同じ特性を持つ。
では実際にどう使うのかを紹介しよう。
I形断面の断面二次モーメント、平行軸バージョン
では上で解法を説明したのと全く同じI形断面の断面二次モーメントを考える。

平行軸の定理の考え方を利用して考えると下の図の考え方ができる。
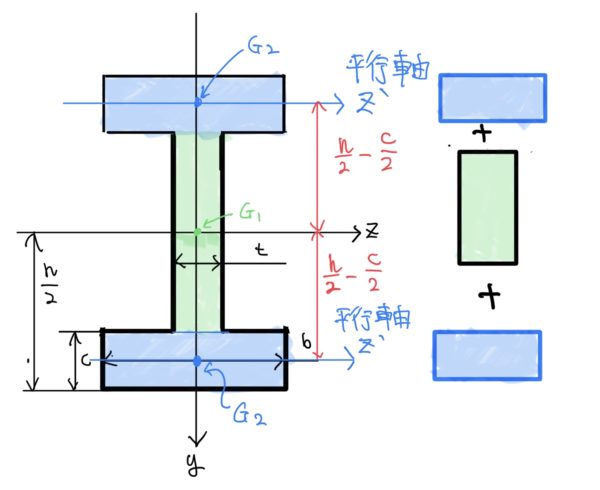
ではまず真ん中の図の緑の棒の断面二次モーメントIzは棒の断面二次モーメント$ \frac{bh^3}{12} $より
$ Iz=\frac{t(h-2c)^3}{12} $
図の青色の四角1個の断面二次モーメントIz’をz‘軸周りで考えると上と同じで
$ Iz’=\frac{bc^3}{12} $
となる。
ここで平行軸の定理を使って緑色の断面二次モーメントをz軸周りに変換する。
青の棒の面積はbc、軸間の距離は$\frac{h-c}{2} $なので平行軸の定理より
$ Iz=Iz’+e^2A=\frac{bc^3}{12}+(\frac{(h-c)}{2})^2bc=\frac{bc(3h^2-6hc+4c^2)}{12} $
となりトータルでは青い部分の断面二次モーメントと緑の部分2個分の断面二次モーメントを足すと(計算を省く)
$ Iz=\frac{bh^3}{12}-\frac{(b-c)(h-2c)^3}{12} $
で割と楽に求められる。
まとめ
ここまで断面1次モーメントの計算、図心の求め方と断面2次モーメントの計算、断面2軸極モーメント、平行軸の定理を説明してきた。
・図心(中立面)を原点とした座標軸での断面一次モーメントは0になる。
・図心は断面一次モーメントから面積で割れば求まる(逆も成り立つ)。
・断面二次モーメントは軸に関する微小面積を定義して面積で積分すれば求まる。
・四角断面の断面二次モーメントは$ \frac{bh^3}{12} $(h方向に関する)で求まる。
・丸断面の断面二次モーメントは$ \frac{πd^4}{64} $で求まる(dは直径)。
ほとんどの構造物の断面は丸と四角の組み合わせでできておりどんなに複雑でも丸と四角の断面二次モーメントを覚えておけば平行軸の定理を使って求められる。
後に別ページで代表的な断面の断面2次モーメントを紹介する。
今の時代ではCADなりで求まるので自分で計算することはほぼない。
ただし断面二次モーメントは軸方向に寸法を大きくすると3乗で大きくなる(丸軸だったら4乗)ので荷重方向と設計した構造物の断面の寸法を確認しておこう。
どんなに幅を取ってもあまり意味がなく高さ方向に大きい寸法を取ろう。
これで終わりにする。次回は梁の撓み(たわみ)を求めていく。
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
個人的なお勧めで私はエアソフト本体やパーツ関連の多くをアマゾンのプライム会員に入って購入しています。
意外と本体、パーツ共にラインナップが充実していて最安値では無いもののそこそこの低価格で安定的に購入できるので重宝しています(小物だと買いに行くのがめんどくさいので重宝)。
多くの商品が配送料無料、お急ぎ便無料になり速ければ次の日に到着します。さらに会員になると映画、アニメ、音楽、書籍なども多くの作品がフリーで見れます。
月間プランだと月600円からで年間プランだと年で5900円でかなりのお得で会員は対象商品購入(エアソフト関連も大抵、対象になっている)でポイントが還元されます。
まずは無料体験からお勧めします。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。






コメント