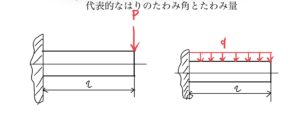
前回ははりのたわみを簡単に求める方法を解説した。
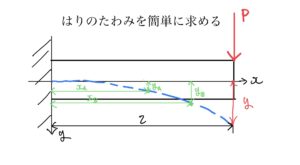
今回は以前にトラスの不静定問題のようなはりにおける不静定問題の解法を紹介する。さらに異種材料が組み合った組み合わせはりの考え方も紹介する。
今回の紹介する方法は昨今のシミレーション事情から実際に使ってたわみ量を求めることはほとんどないと思う。
ただしひレイアウト、スケッチなどの構想段階で構造物の変形量を想像するのに役に立つのでよく理解して欲しい。
また後半の組み合わせはりについては昨今では異種材料を組み合わせて強度、剛性の向上を図ることが非常に多い。よって概念はよく知っておいて欲しい。複合材は今後も利用が指数関数的に増えるはずだ。
これもシミレーションで求めてしまうので実際に計算することはほとんど無いだろうが意味を理解していないとシミレーションが正しく行えない。
いずれにせよ実際に使わなくてもわかってないと困ることは多々あるので是非、理解しよう。
はりの不静定問題
そもそも静定問題、不静定問題って何だというのはトラスでも説明したがもう一度、説明しておく。
静定とは応力、変形量を求める際に外力の釣り合い(力、モーメント)と内力の釣り合い(応力、剪断力)だけで求められることである。
一方で不静定とは外力、内力の釣り合いだけでは応力、変形量が求められずさらなる幾何学的な変形量の関係などの条件がわからないと求められないことである。
毎度のことながら名前はどうでも良いのだが要は、力の釣り合いだけで求まるかどうかの違いである。
今回ははりの不静定問題を取り扱っていく。
静定、不静定問題は以前のページで紹介しているので気になる人は覗いてみて欲しい。
はりの不静定問題
いつもながらの例題を設定していこう。
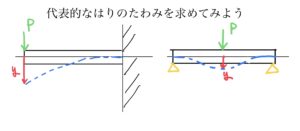
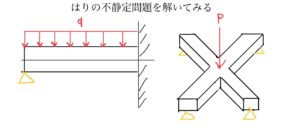
先端が台座Aで支えられて逆側が壁に固定されている長さlのはりがある。そこに一様な等分布荷重qが掛かっているはりのたわみとたわみ角を求めていく。
座標は、左端を原点とする。
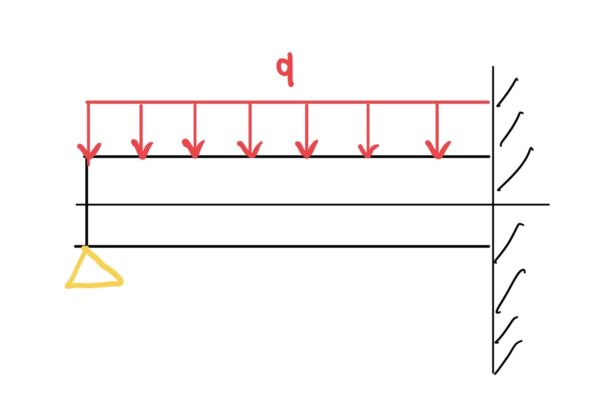
これをいつも通り力の釣り合い、モーメントの釣り合いを考えると次のようになる(RA、RB、MBは未知数)。
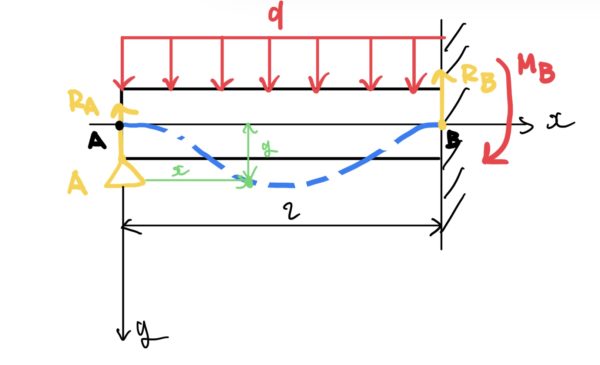
力の釣り合いを考えると
$ RA+RB=ql $
次にA点周りのモーメントの釣り合いを考える
$ MB-RBl+\frac{ql^2}{2}=0 $
ここでいつもなら未知数RA、RB、MBを求めるのだが変数3つに対し式が2つしかないので求められない。これが外力の釣り合いで求められない不静定問題になる。
求められないのは仕方がないので未知数はRA、RB、MBのまま進める。
任意の座標xでの曲げモーメントを考える。
$ M=\frac{q}{2}x^2+RAx $
上の式をたわみの微分方程式に代入する。
$ \frac{d^2y}{dx^2}=\frac{1}{EI}(\frac{q}{x^2}-RAx) $
これを解くと
$ \frac{d^2y}{dx^2}=\frac{1}{EI}(\frac{q}{6}x^3-\frac{RA}{6}x2+C1) $
$ y=\frac{1}{EI}(\frac{q}{24}x^4-\frac{RA}{6}x^3+C1x+C2) $
ここでいつも通りはりの境界条件からC1、C2を求める。境界条件ははりの左端(x=0)でたわみ量0、右端(x=l)でたわみ角が0だ。
$ C1=-\frac{ql^3}{6}+\frac{RAl^2}{2}、C2=0 $
いつもならここではりのたわみ角、たわみ量の式が求められるのだがこの例題では未知数RA、RB、MBが残っている。上記の通り力の釣り合い、モーメントの釣り合いの2つでは足りないのでたわみ量の式に境界条件のはりの右端(x=l)でたわみ量0を使うと解ける(不静定問題を解くための幾何学条件)。
$ RA=\frac{3}{8}ql、RB=\frac{5}{8}ql、MB=\frac{1}{8}ql^2 $
これをたわみ角、たわみ量の式に代入する。
$ たわみ角θ=\frac{q}{48EI}(8x^3-9lx^2+l^3)、たわみ量y=\frac{q}{48EI}(2x^4-3lx^3+l^3x) $
このように外力の変数に対し釣り合いの式が足らないのでたわみの式を利用して幾何学的な拘束をして解いて行くのだ。
ただし不静定問題だと立てる式、計算が静定問題に対し増加するので計算が非常に面倒である。そこで簡単に求められる方法を紹介する。
重ね合わせ法
先程の例題と全く同一のはりを考える。

このときにはりにかかる外力は等分布荷重qと台座Aから受ける反力RAになる。
実はそれらをそれぞれ一つずつのはりの問題として考えて後で結果を足すことができる。これを重ね合わせ法という。
qとRAではりを分ける。
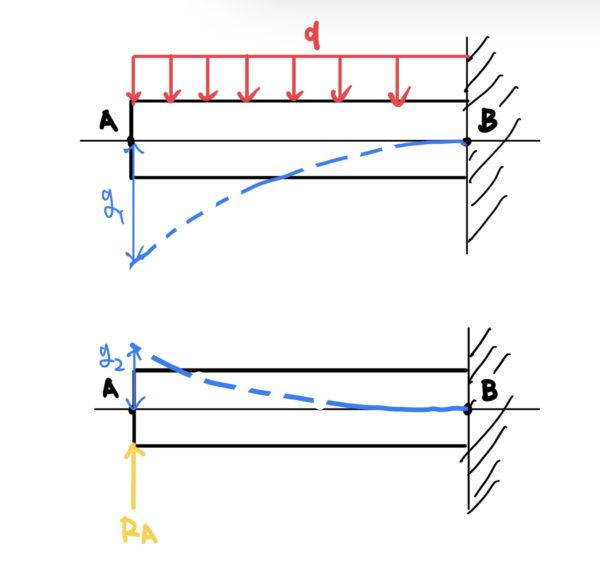
それぞれが単純な片持ちはりの問題に分けることができる。これらのたわみは以前に紹介した重積分法や面積モーメント法で簡単に求まる。
そうするとそれぞれの先端でのたわみy1、y2はそれぞれ次の式になる。
$ y1=\frac{q}{24EI}(x^4-4l^3x+3l^4) $
$ y2=-\frac{RA}{6EI}(x^3-3l^2x+2l^3) $
それぞれの単純なはりのたわみを足すと元のはりのたわみ量になる。これを重ね合わせ法と呼ぶのだ。
まだRAがわからないので不静定問題を解く条件としてはりの左端x=0の時、たわみは0になるので
$ y=y1+y2=\frac{ql^4}{8EI}-\frac{RAl^3}{3EI}=0 $
より$ RA=\frac{3}{8}ql $になり固定端Bの反力RB、MBは力の釣り合いと先端Aのモーメントの釣り合いから
$ RA+RB=ql $
$ MB-RBl+\frac{ql^2}{2}=0 $
より$ RB=\frac{5}{8}ql $ $MB=\frac{1}{8}ql^2 $よりたわみは、次の式で求まる。
$ y=y1+y2=\frac{q}{48EI}(2x^4-3lx^3+l^3x) $
そう、割と簡単に求まるのだ。
y1、y2のたわみを求めるときに割と単純な曲げモーメントになるので重積分法ではなく面積モーメント法を使うことをオススメする。

もう一例ほど紹介しよう。これは筆者が学生時代に頭を悩ませた問題だ。
はりの不静定問題2
ではまず例題を設定しよう。長さlの両持ちはりが✖️字のように組み合って交点に荷重Pがかかるとしよう。
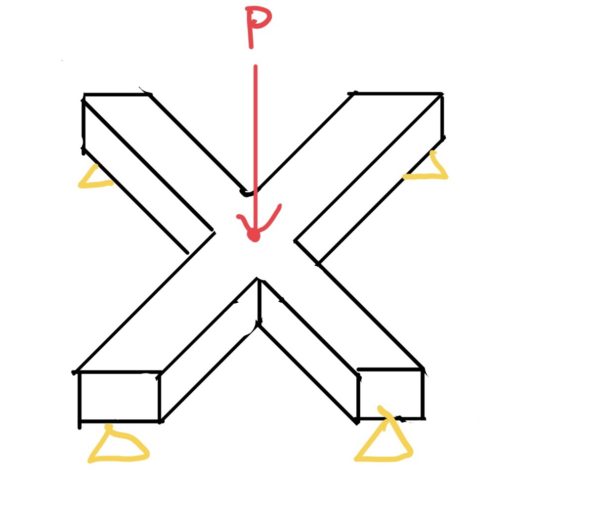
これを計算しやすい図に直すと各台座にA、B、C、Dと名前をつける。
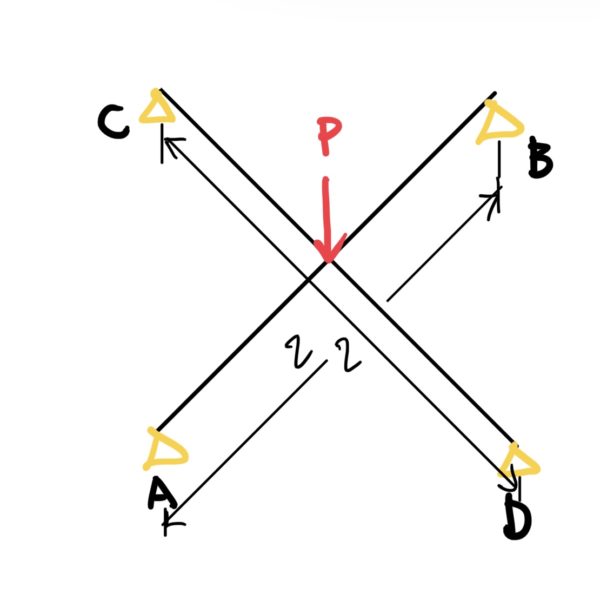
ここからは重ね合せ法を使うためにはりABとCDに分けて考える。それぞれの荷重はP1、P2と置くと(断面二次モーメントがそれぞれ異なることにしよう)
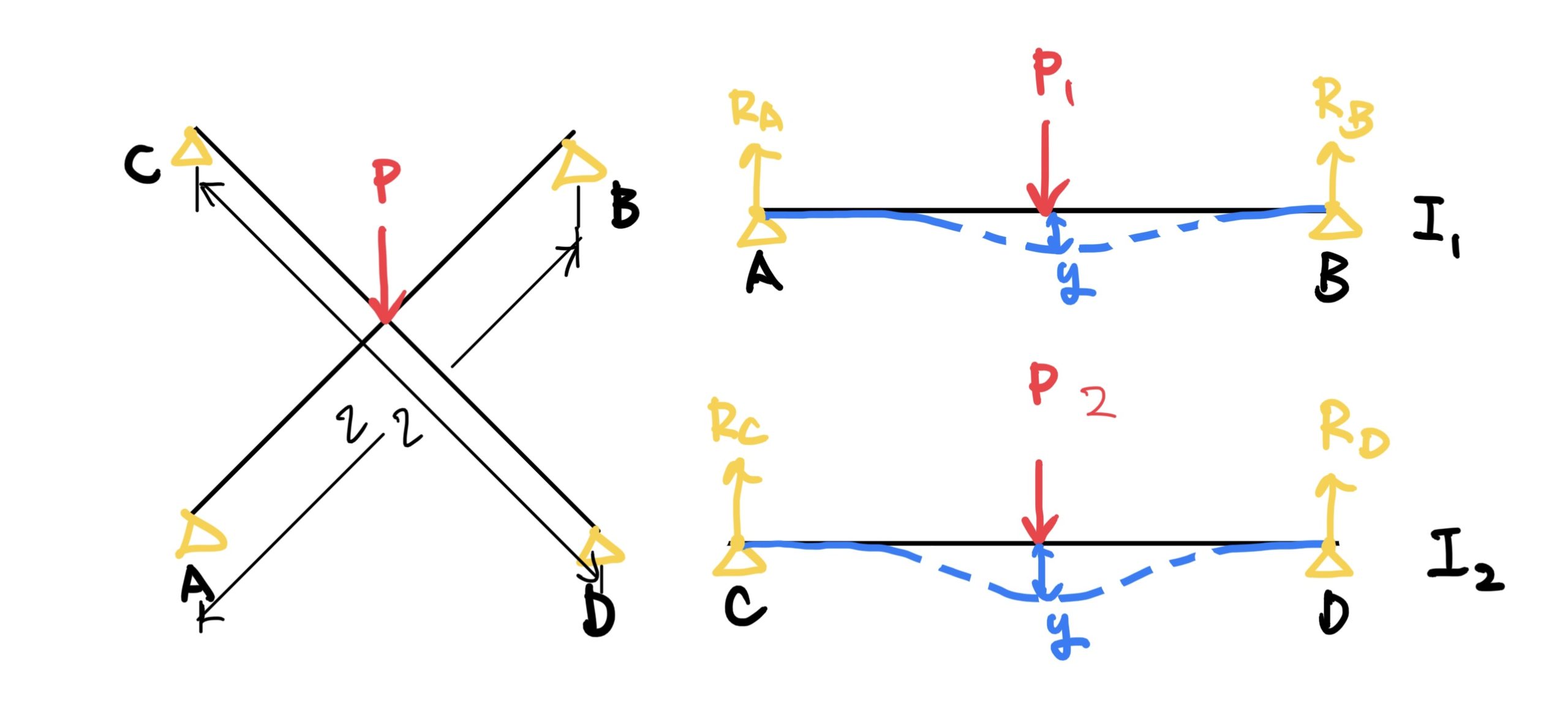
これで簡単な両持ちはりになる。ではそれぞれの最大たわみ量y1、y2を求めると
$ y1=\frac{P1l^3}{48EI1}、y2=\frac{P2l^3}{48EI2}(それぞれの最大たわみが発生する場所ははりの中央) $
ここから重ね合せの条件を考えると荷重は$ P=P1+P2 $、はりABとCDが交わっているのたわみ量は同じなので$ y1=y2 $となる。(不静定問題の幾何学的な拘束)
$ P1=P-P2とy1=y2より\frac{P1}{I1}=\frac{P2}{I2} $
$ P1=\frac{I1}{I1+I2}P、 P2=\frac{I2}{I1+I2}P$
となりたわみ角、たわみ量や各台座での反力RA、RB、RC、RDは簡単に求まる。
これではりの不静定問題の紹介を終わりにする。
組み合わせはり
ここからは異種材料を組み合わせた場合のはりを考えてみる。
実際の設計や製品では筆者の知るところではアルミと鉄の組み合わせを使うことがかなり多い。他には樹脂と銅、カーボンファイバーと樹脂(CFRPってやつ)で変わり種ではチタン、マグネシウムなどを圧入や接着などを使って一つの部品にしたり部材にすることがある。
このような材料を複合材料と呼ぶ。
上手い組み合わせ材料で複合材料を作るとそれぞれの材料が互いの欠点を消し合って非常に使える材料になることがある(高価だけど)
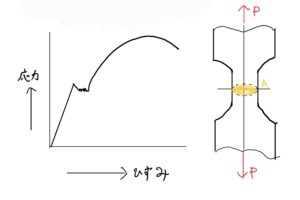
ただしあまりにも材料の物性が異なる(材料の特性 応力-歪み線図)場合は変形している途中で異種部材が剥がれるたり滑ったりして意味がなくなり。(密着性、剥離)。
このような研究は素材メーカーは、もちろんだが意外と日本の大学、企業はかなり頑張っていて世界でもトップクラスの実力を持つ。
このように複合材料は素晴らしい材料なのだが異種部材で構成されているので強度計算を実施するときに各材料毎の弾性係数、断面を考えて計算するのは非常に面倒である。
そこで複合材を一つの部材と見て仮想の断面二次モーメントを求める。
複合材の仮想の断面二次モーメントを求める
いつも通り例題を設定しよう。
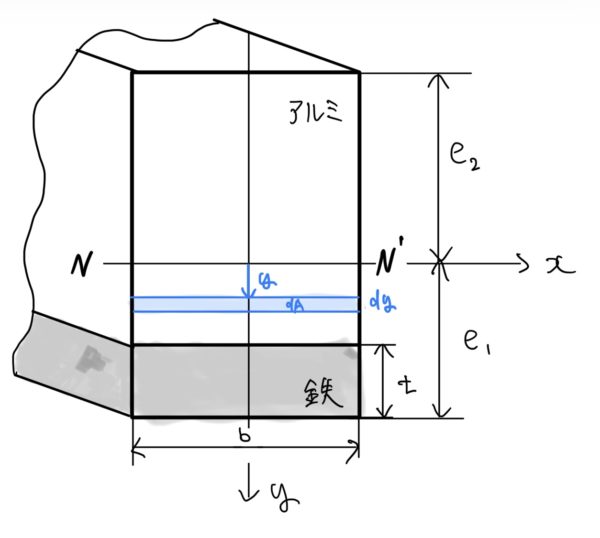
下の図の寸法の角材で主要部材がアルミ、底の厚さtが鉄のはりを考える。このときのアルミの弾性係数をEa、鉄の弾性係数をEfとしよう。もちろんアルミより鉄のが強いのでEf>Eaにも注意しよう。
ここで仮想的な断面2次モーメントを考えていこう。
断面2次モーメントを求めるので以前に紹介した初心者でもわかる断面1次モーメントと断面2次モーメントと同じようにはりの断面内の曲げ応力、曲げモーメントを考えて求めて行く。
まず例題の断面に発生する任意の距離yでの曲げ応力を考えていこう。
はりがたわんだ時の曲率半径をρとすると曲げ応力は以下のように表せる。
$ アルミ部材内の曲げ応力σa=\frac{Ea}{ρ}y $
$ 鉄部材内の曲げ応力σf=\frac{Ef}{ρ}y $
微小面積dA=bdyに働く力は、
$ アルミ部材内の微小面積に掛かる荷重dPa=\frac{Ea}{ρ}ybdy $
$ 鉄部材内の微小面積に掛かる荷重dPf=\frac{Ef}{ρ}ybdy $
となる。
ここで同一断面内での曲げ応力は総和が0、曲げ応力モーメントは曲げ応力によって発生することを思い出して欲しい。
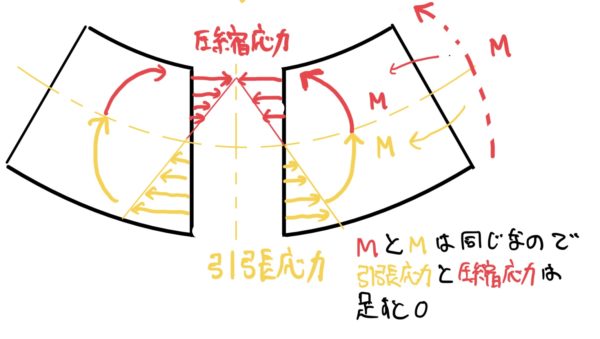
このことを式にすると
$ 曲げ応力の総和 \int_{-e1}^{e2-t} dPa+\int_{e2-t}^{e2} dPf=0 $
$ 曲げ応力によるモーメント \int_{-e1}^{e2-t} ydPa+\int_{e2-t}^{e2}ydPw=M $
上の式をそのままアルミと鉄部分を分けて計算しても良いのだが面倒なので少し工夫しよう。2つに分かれている材質を算数的なテクニックを使って仮想的にどちか一方の材質でまとめて表して行くことを考える。
今回は鉄に統一する(どちらでも良い)。アルミ部材内の微小断面積の荷重の式をアルミの弾性係数と幅を弄って無理やり鉄の弾性係数で表してみる。
$ アルミ部材内の微小断面積の荷重dPa=\frac{Ea}{ρ}(\frac{Ef}{Ef})ybdy=\frac{Ef}{ρ}(\frac{Ea}{Ef}b)ydy $
上の式の$ \frac{Ea}{Ef}b $を仮想的な断面の幅と考えるとアルミ部分は幅が$ \frac{Ea}{Ef}b $の鉄と考えることができる。
この性質を使って曲げ応力の総和の式を書き直すと
$ \int dPa+\int dPf=\int_{-e1}^{e2-t} \frac{Ea}{ρ}ybdy+\int_{e2-t}^{e2} \frac{Ef}{ρ}ybdy=\frac{Ef}{ρ}(\int_{-e1}^{e2-t} \frac{Ea}{Ef}bydy+\int_{e2-t}^{e2} bydy) $
この式の$ \int_{-e1}^{e2-t} \frac{Ea}{Ef}bydy+\int_{e2-t}^{e2}bydy $は断面を一様な鉄と見做したときの断面1次モーメントにできる。
同様に曲げ応力によるモーメントの式についても書き直すと
$ \int_{-e1}^{e2-t} ydPa+\int_{e2-t}^{e2}ydPw=\int_{-e1}^{e2-t} \frac{Ea}{ρ}y^2bdy+\int_{e2-t}^{e2} \frac{Ef}{ρ}y^2bdy=\frac{Ef}{ρ}(\int_{-e1}^{e2-t} \frac{Ea}{Ef}by^2dy+\int_{e2-t}^{e2} by^2dy)=M $
この式の$ \int_{-e1}^{e2-t} \frac{Ea}{Ef}by^2dy+\int_{e2-t}^{e2} by^2dy $は断面を一様な鉄と見做したときの断面2次モーメントにできる。
このことを図に表すと以下のようになる。
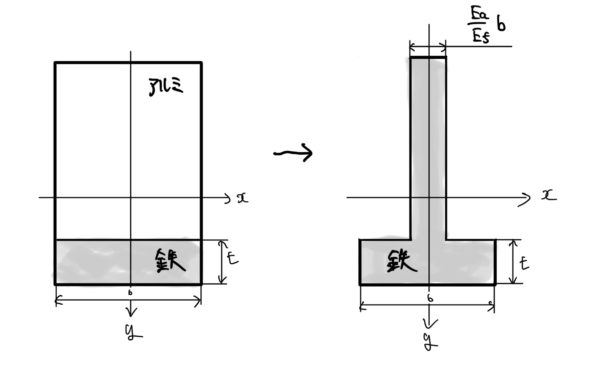
つまりアルミと鉄を使った部材を高さ方向はそのままでアルミ部の幅を$ \frac{Ea}{Ef}b $とすることで一様な鉄の部材と見做すことができるのだ。
この変換した断面二次モーメントを等価断面と呼ぶ。
ここで等価断面の断面2次モーメントをIと置いて断面二次モーメントの特性を使うと次の式で部材の上端での応力、下端での応力σ2を表せる。
$ 上端の応力σ1=-\frac{M}{I}e1(アルミ部) $
$ 下端の応力σ2=\frac{M}{I}e2(鉄部) $
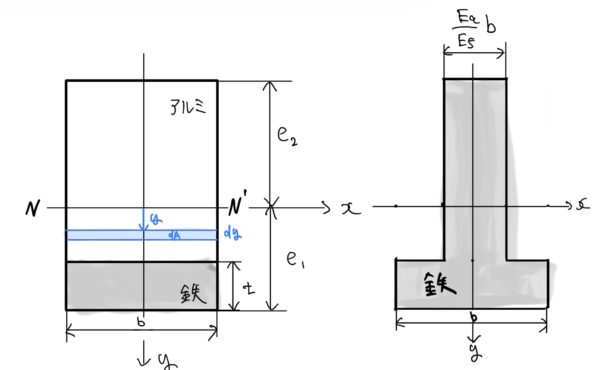
ここで注意なのだが弾性係数の違いを仮想の幅で吸収しているのではりの変形、歪みは等価として扱えるが曲げ応力に関しては元の部材に対するものを正確に表したものではない。
なので上端での応力(アルミ部)は上の式で表せないので歪みの等価を利用して求め直す。
$ \frac{σ1a}{Ea}=\frac{σ1}{Ef}(アルミ部の歪みと等価断面の歪みが等しい)、σ1a=-\frac{Ea}{Ef}\frac{M}{I}e2 $
これは複合材で断面二次モーメントを部材毎に複数計算するのが面倒なときに一つにまとめられるので楽である。また2種類ではなく何種類でもこの方法が使えるので幾重にもラミネート加工された部材に最適な手法だと思う。
まとめ
今回も設計現場で頻繁に使ううようなものではないが概念は理解しておいて欲しい。
レイアウトやスケッチなどの構想するときに役に立つ。
・はりの不静定問題を解くときは外力、ない力の釣り合いに加えてはりのたわみ角たわみ量の幾何学的な関係式も考えるようにしよう。
・はりに複数種類の荷重が加わるときそれぞれを分解して考え、後に足し合わせることができる。
・複数種類の材料が組み合った部材は、仮想の一つの断面に置き換えられる。
このくらいを理解しておけば大丈夫だ。
特に複合材は絶対に今後、採用が増加していくのでイメージできると便利である。
ここまででようやくはりのほとんどが説明できた。
次回ははりの総まとめとして代表的な断面の断面二次モーメントと代表的なはりのたわみのデータ集を紹介する。
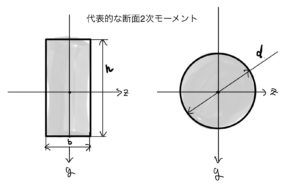
これらの次にようやく材料の破壊の入門で座屈を説明しよう。
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。






コメント