前回の円環応力、トラスの説明で案内したとおり今回から梁(はり)の説明に入る。
機械設計において梁の検討は最も重要なことの一つで頻繁に使う。
また材料力学の前半から中盤にかけての一大イベントに当たる。
様々な新しい概念が出てくるが今までの説明をしっかり理解していれば理解できるはずだ。
是非、頑張ってついてきてくれ。
梁(はり)って何?
まずそもそも梁とは何かを説明すると日本家屋に見られる梁や機械設計ではリブを梁と見立てたりする。
他には公園の遊具のシーソーとかありとあらゆる構造物に存在する。
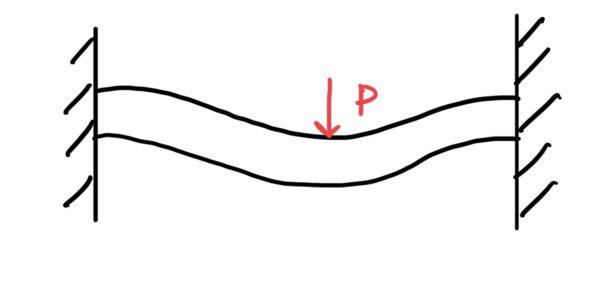
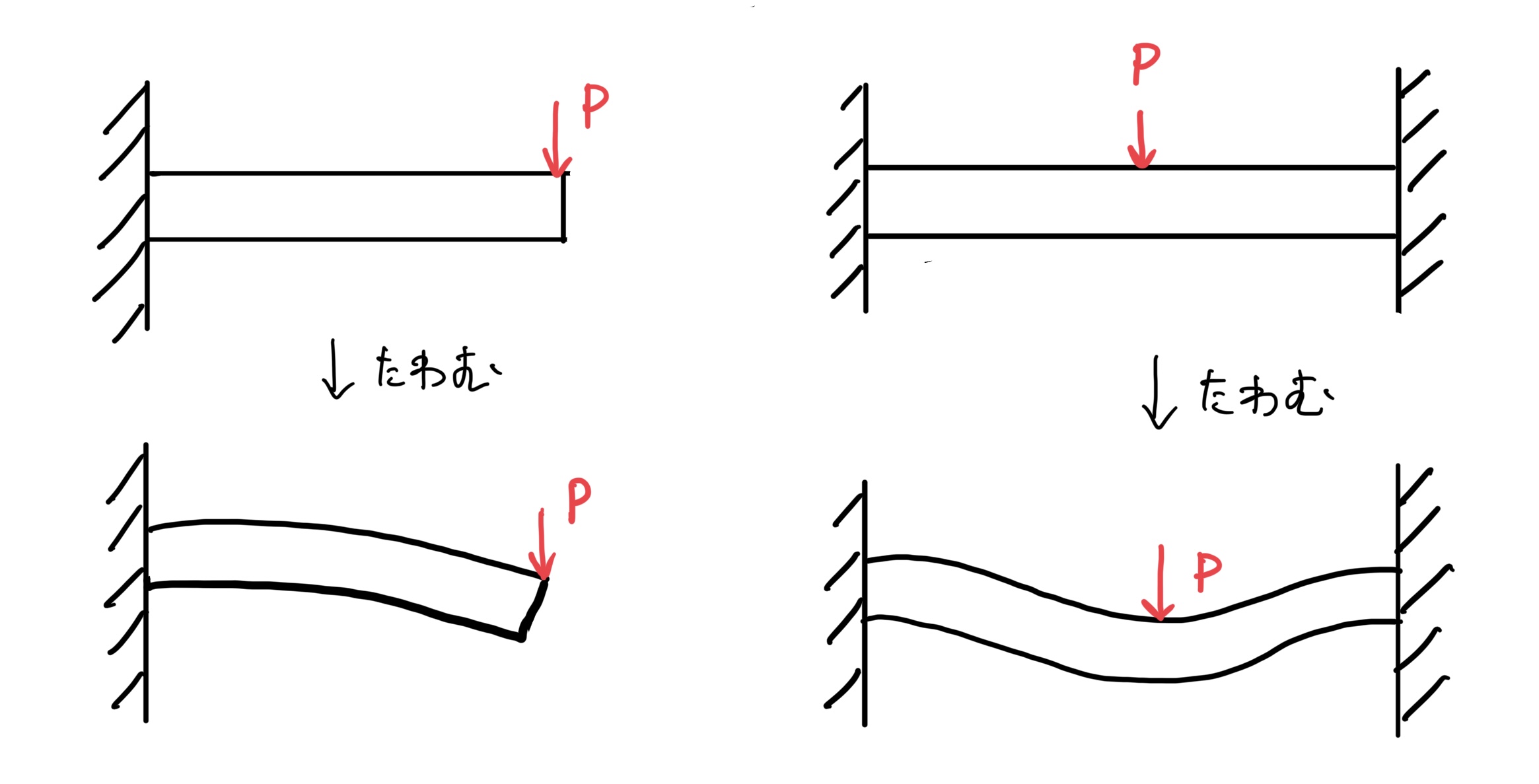
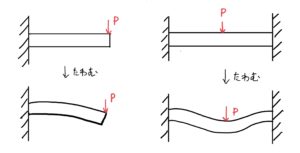
まず代表的な梁は片側で棒を支えている片持ち支持梁だ。

想像してもらうと次の図のように撓む(たわむ)。

次に代表的なのが棒の両端を支えている両持ち支持梁だ。
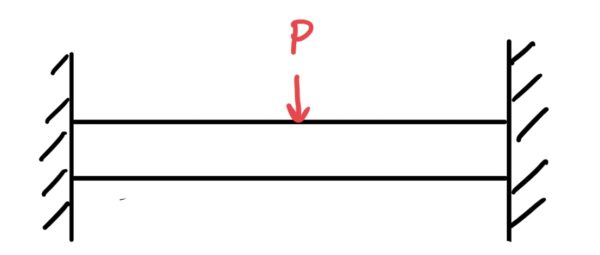
これも想像すると真ん中がへこむように撓むことが容易にできると思う。
他にも呼び方が決まっている梁はあるのだがまず基本のこの二つをしっかり理解して欲しい。
ここまで当たり前のことじゃないかと思う方が多いと思うのだが構造物を設計するとこの2パターンが複雑に絡み合った形状になりわからなくなってしまう。
逆にいえばどんなに複雑な構造物でも一つ一つ丁寧に分解していけばほぼ紹介した2パターンに分けられる。
分解したこの2パターンで考えれば多くの構造物の応力分布、変形がよくわかるのだ。
次に梁の外力と内力の関係を見ていこう。
梁に働く剪断力、曲げモーメント
ここからは簡単な片持ちはりの例題を見ながら剪断力と曲げモーメントを考えていく。
外力が片持ち支持梁の先端に荷重P、座標を片持ち梁の先端を原点として平行方向をx、鉛直方向をyと設定する。各向きは図の通り。
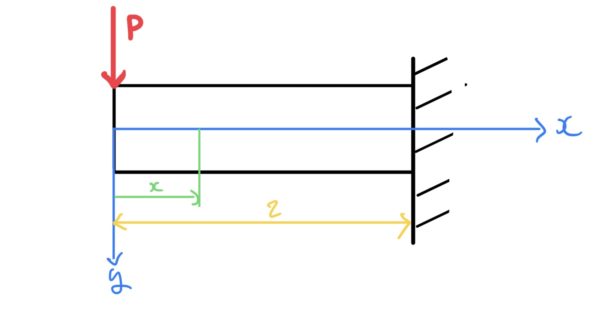
ここで任意の位置xで梁をカットした場合を考えてみる。カットした断面には外力との釣り合いから力が働く。断面に発生する力は断面に対して水平なので剪断力になる。
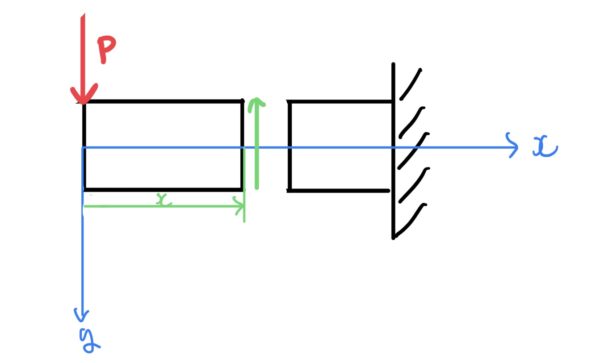
次に上と同じ任意の位置xでのモーメントを考える。カットした断面にははりの荷重Pによって発生するモーメントに対抗するモーメントが発生する(はりはたわむが回転はしない)。これを曲げモーメント呼ぶ。
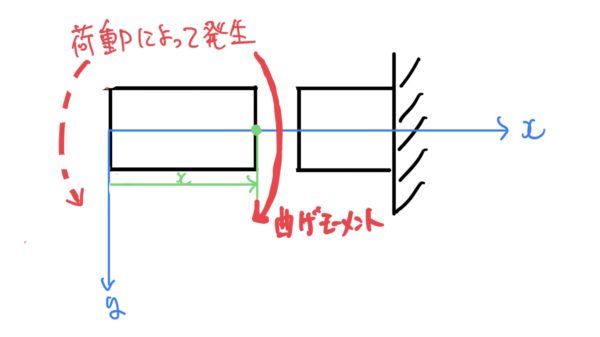
このように例題のような単純な片持ち支持はりの任意の断面内には剪断力と曲げモーメントが発生するのだ。
発生した剪断力と曲げモーメントについて具体的に考える前に一つだけ大切なことを説明する。
大切なこととは任意の断面に発生する剪断力と曲げモーメントの符号のルールだ。
はりの断面に発生する剪断力、曲げモーメントの符号のルール(超重要ポイント!!)
以前の記事で剪断力の符号は基本的に+であることを述べた。モーメントは物理学の定義では時計回りが+と定義されている。
上記のような一般常識とは異なるルールがはりの断面内にはあるので説明していこう。
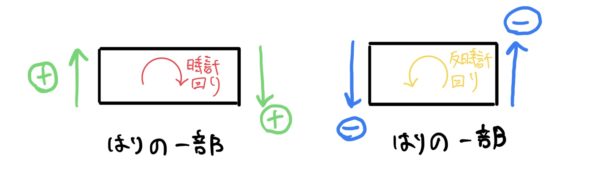
まずはりの断面に発生する剪断力の符号はその断面が時計回りに発生する方向を+とする。
言葉だけでは分かりにくいので図解しよう。
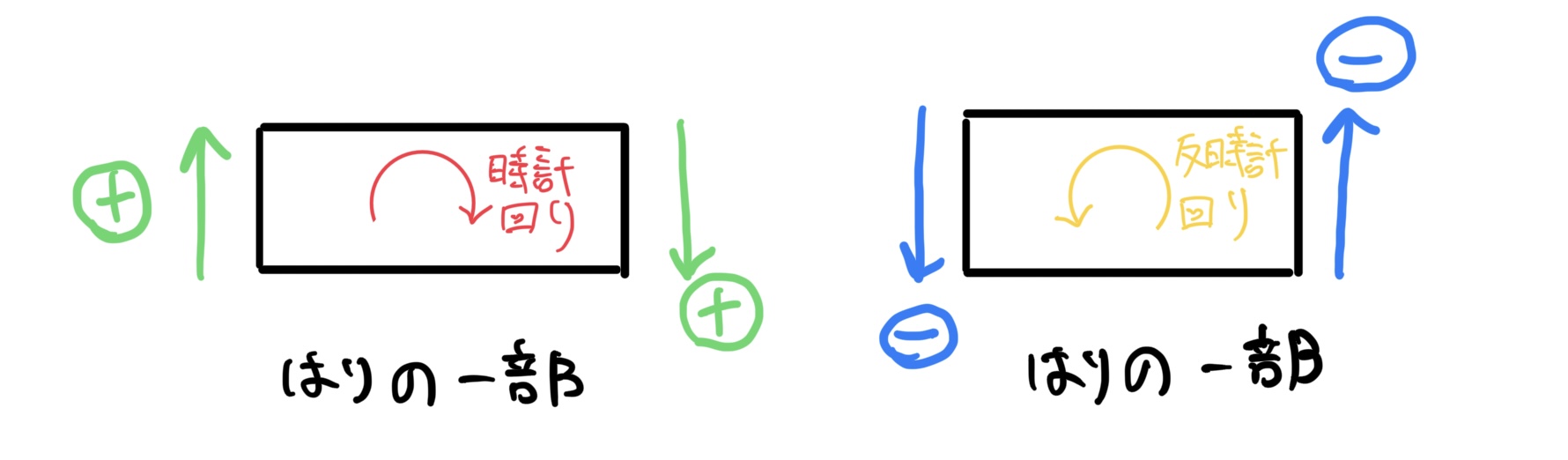
はりの断面に発生する曲げモーメントの符号はその断面が上に凹なる向きが+とする。
曲げモーメントも図解しよう。
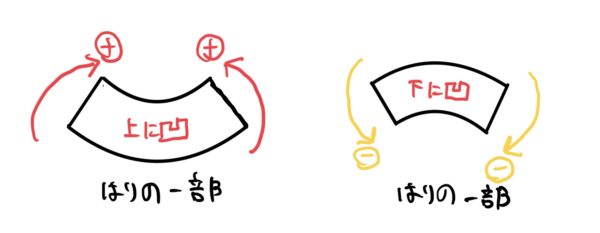
とても大切な符合なのだが物理の常識と異なるしややこしいので間違いやすいのでしっかり理解しておこう。筆者もよく間違える。
しつこいが剪断力は時計回りが+、曲げモーメントは上に凹が+と頭に入れておこう。
折角なので片持ちはりを例に任意の断面での剪断力と曲げモーメントの符号を図にしておく。
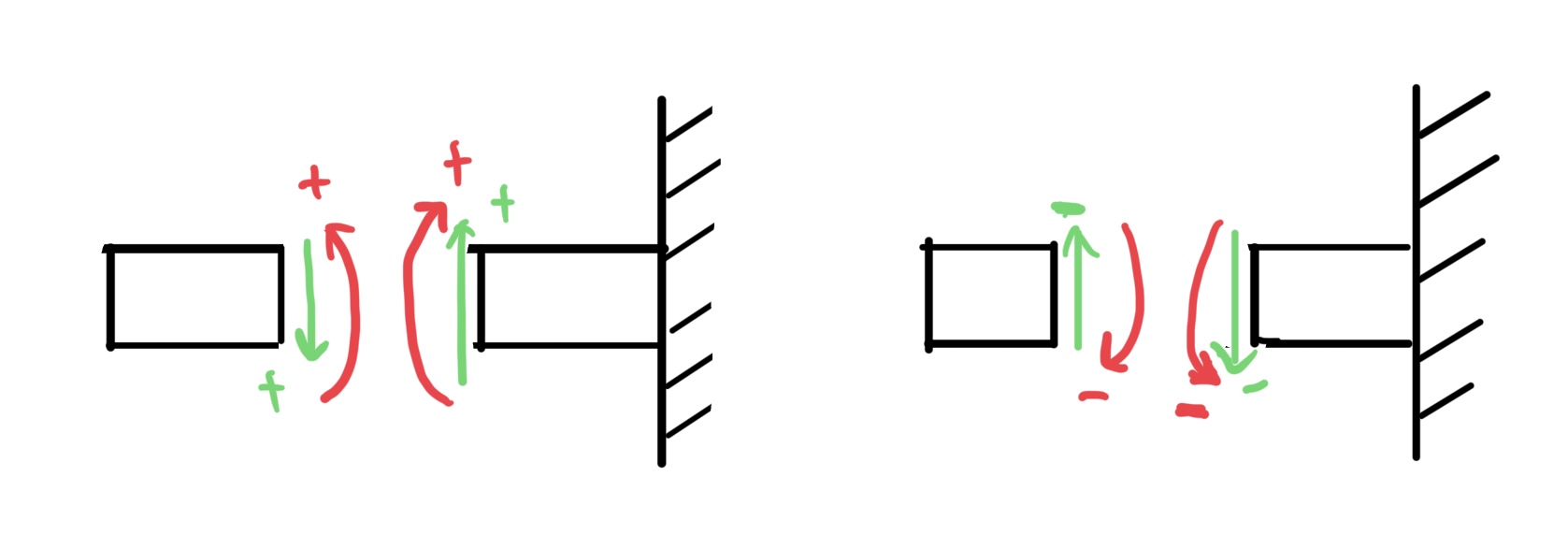
応力の説明でも符合の大切さを述べたつもりだが物理学をはじめとする工学の世界ではこの符合がとても大切なのである。
場合によっては、値より符合が合っている方が良かったりする場合も多い。筆者は学生時代に符合を舐めていて授業の単位を数多く落とした。逆に設計者になってから間違えている人もいて見てて悲惨だったのを覚えている。
このような符合の感覚はとても大切なので身につけておこう。
ここまでで定義が揃ったので力の関係式を立てていく
外力と内力の関係
ここでやっと最初に定義した片持ち支持はりの剪断力、曲げモーメントについて考えていこう。
まずは力の釣り合いを考えておこう。

外力である荷重Pが剪断力Qを発生させるので次の式が成り立つ。(符合に注意)
$ 荷重Q=-P(剪断力) $ 剪断力は反時計回り方向なのでー。
次に断面でのモーメントの釣り合いを考える。

外力である荷重Pによって発生するモーメントに対抗するから次の式が成り立つ(符合に注意)。
$ 曲げモーメントM=-Px(荷重によるモーメント) $ モーメントは下に凹なのでー
次に上記で定義した剪断力と曲げモーメントを図で表してみる。
まずは剪断力の図。
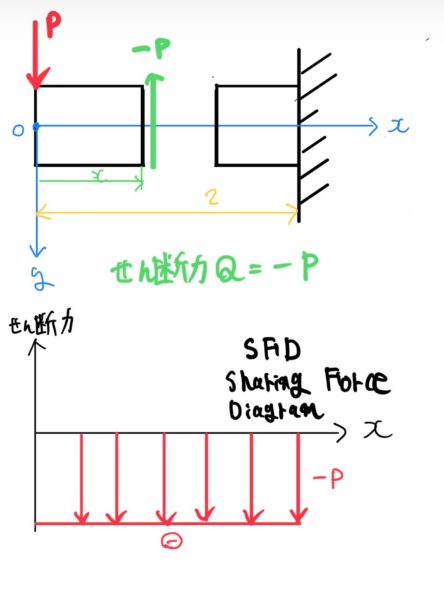
上のように剪断力を図示したものを剪断力図(Sharing Force Diagram SFD)と呼ぶ。図を見ると当たり前だが剪断力は距離に寄らず一定のままだ。
次に曲げモーメントの図を見て行こう。
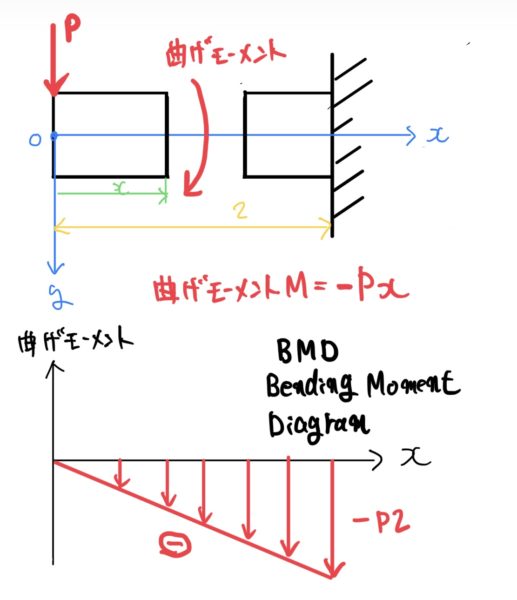
曲げモーメントを図示したものを曲げモーメント図(Bending Moment Diagram BMD)と呼ぶ。図を見ると距離によって曲げモーメント量が変化し長さlの右端部でMAXになる。曲げモーメントがMAXになる断面を危険断面と呼ぶが筆者は実際の設計現場で使ったことがない。
例題のような単純な梁では当たり前に感じてわざわざ図にする意味を感じないと思うが複雑な荷重が絡み合うと意外なところに曲げ応力が重なる場合があるので面倒がらずに図にすることをオススメする。
また撓み(たわみ)について今後、詳しく説明していくが変形量が大きいところが曲げモーメントの最大ではなく、変形量が小さい、もしくは0のところが曲げモーメントが最大だったりする。
このような感覚は設計にとって重要なので身につけよう。
ここまで片持ち支持梁で説明してきたが次に多くのパターンで考えられるように少し一般化する。
荷重と剪断力、曲げモーメントの関係
梁の力の関係を一般化するに当たって次のような例題を設定する。
とある梁の微小区間dxを切り取ってその区間に外力である等分布荷重q(x)[N/mm](圧力のような力)が掛かる。
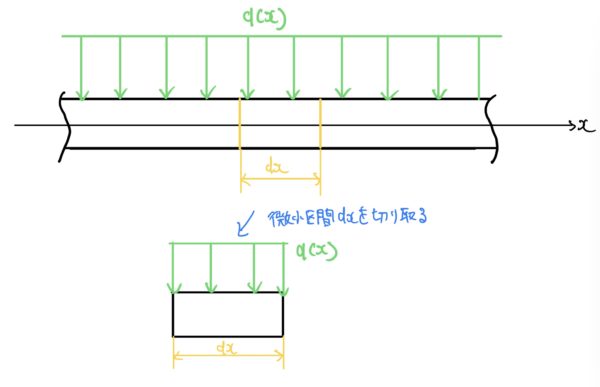
その時に発生する左断面の剪断力をQとし右断面をQ+dQ、曲げモーメントの左断面をMとし右断面をM+dMとする。
ここでもせん断力、曲げモーメントが+になる向きに仮置きしただけで実際の符合は計算で求めていく。
切り取ったはりの一部の断面に働く力とモーメントを見ていこう。
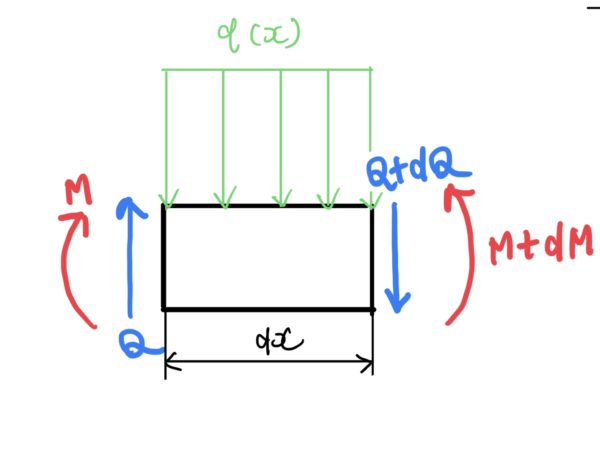
ここで力の関係式を立てる。ここでは一般的な力の釣り合いを見ているので符号ははりの符号ルールではなく物理のルールにする。
$ (Q+dQ)-Q+q(x)dx=0 $
整理すると
$ \frac{dQ}{dx}=-q(x) $
つまり剪断力Qを距離xで微分すると等分布荷重-q(x)になるのだ。言い換えると剪断力の変化する傾きは等分布荷重と同じということである。
次に右断面でのモーメントの釣り合いを考えると次の式が成り立つ。ここでの符号も物理に従いモーメントは反時計回りを+とする。
q(x)によって発生するモーメントはq(x)dxが微小区間の真ん中で発生すると考える。
$ (M+dM)-M-Qdx-q(x)dx\frac{dx}{2}=0 $
dxとdxは微小な量を掛け算しているのでさらに微小になるので0とみなすと(例えば0.01×0.01=0.0001みたいな感じ)
$ \frac{dM}{dx}=Q $
となる。
これは曲げモーメントを距離xで微分すると剪断力Qになる。つまり曲げモーメント量の変化する傾きは剪断力Qと同じということである。
数学の微分の分野の話になって申し訳ないが$ \frac{dM}{dx}=Q $から言えることはQ=0の時に曲値になる、つまり曲げモーメントの変化の傾きの符号が変わるポイントになる。なので剪断力Qが0になる座標で曲げモーメントが最大、最小値になることが多いのだ。
これが結構、見落としがちで例えばシミレーションで剪断力だけ見て0だから大丈夫と思っていると曲げモーメントがMAXに発生してたりする。危ないので気をつけよう。
文章だけではわかりにくいと思うので例題を設定して解説しよう。
両持ち支持梁の解法例と曲げモーメントの最大
では例をつくろう。
単純な両持ち梁で長さがlで両端がA、Bという台に支えられている。その梁に等分布荷重q(N/$ mm^2 $)が一様に作用している。(作用反作用の法則でA、Bに反力が発生する)
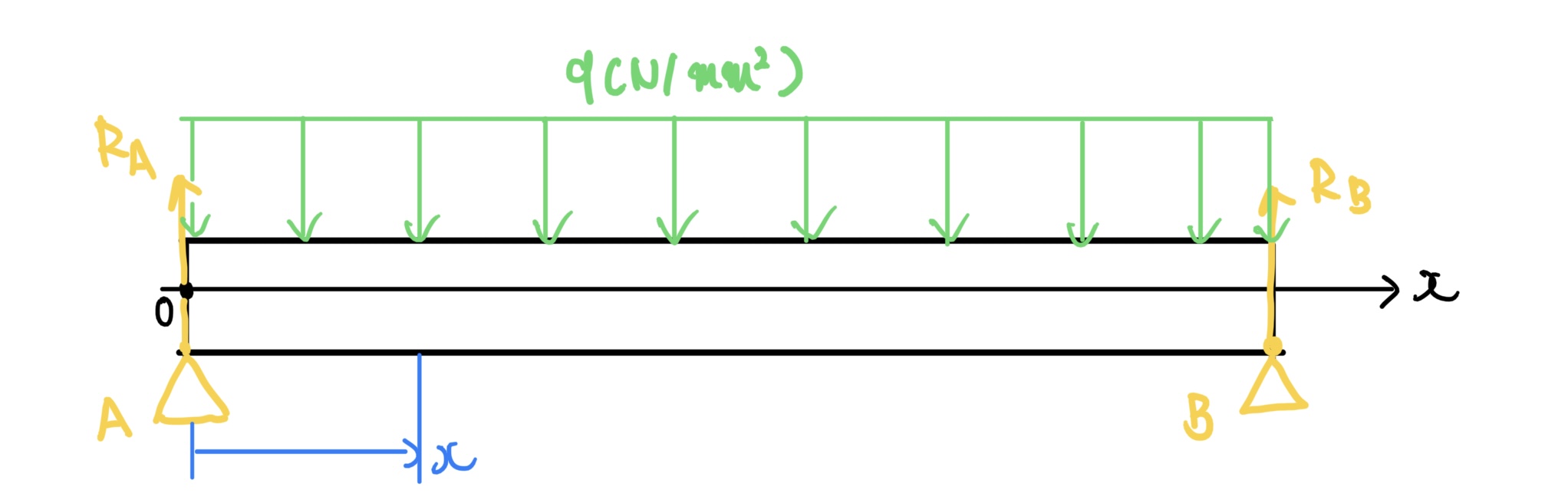
ここで力に釣り合いから次の式が成り立つ
$ RA+RB=ql $
$ RA=RB=\frac{ql}{2} $
次に先ほど説明したように任意の位置xでカットした梁を見ると次のようになる。
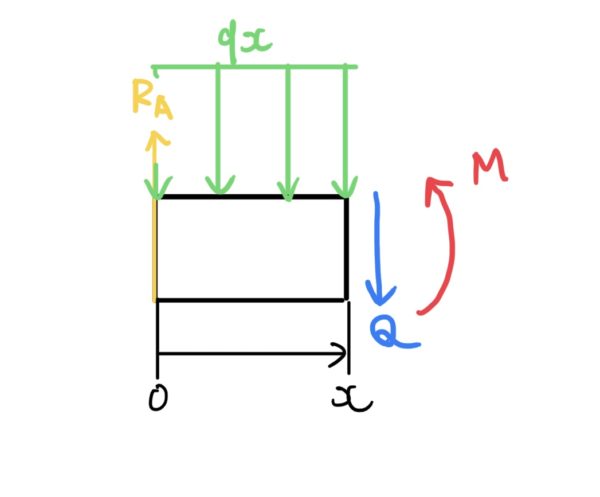
ここから剪断力Qを導くと(符合に注意)
$ Q=RA-qx=q(\frac{l}{2}-x) $
また右断面のモーメントの釣り合いから(符合に注意)
$ M=RAx-qx\frac{x}{2}=\frac{q}{2}x(l-x) $(剪断力Qをxで積分していると同じ)
これらを図示するとSFD、BMDは次のようになる。
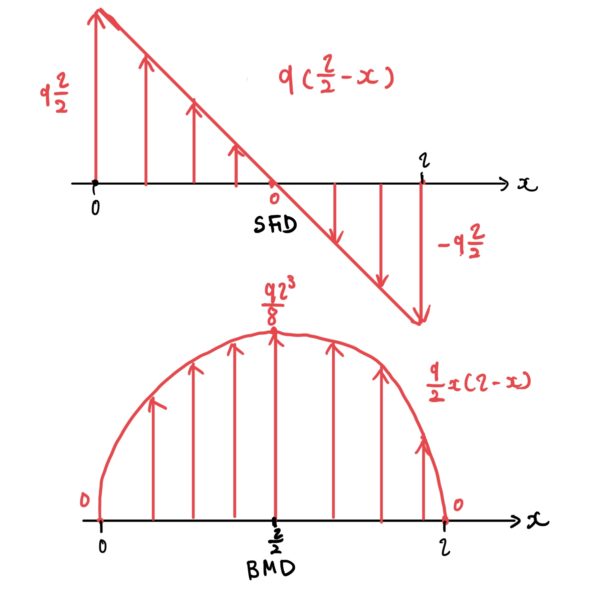
これで剪断力Qが0の時に曲げモーメントが最大になることがわかる。上で述べた剪断力Qの座標で曲げモーメントが最大、最小になることが多いことがわかると思う。
また撓みのところでしっかり説明するが梁の特性として剪断力が0で曲げモーメントが最大の場所が変形量が最大になる。
逆に変形量が0のところは剪断力が最大になっていて結構、危ない場所になる。
つまり後に詳細を説明するがよく言われる剛性が高いということは、変形はあまりしないけれど発生剪断力は非常に高いのだ。
このように変形、剪断力、曲げモーメントの最大、最小値の関係性をイメージできると実践で非常に役に立つのでSFD、BMDを書いてイメージを掴もう。
よく評論家とかが剛性があって良いとか言っているがそれは間違いでプロが唸る設計は部材を均等に変形させて剪断力、曲げモーメントをなるだけ等分布にする構造である。
どうしても寸法変化によって性能が大きく変化してしまう時だけ剛性をあげる。
無駄に剛性が高い構造は設計者のレベルが低いかめんどくさくて検討をサボったかのどちらかである。
剛性を無駄に上げると剪断力が高くなるので耐えられるように面積を増やす、つまり重くなるのだ。重いと当然、性能は落ちるし極端にいえばコストも上がる。バランスが大切なのだ。
この辺の感覚はイメージを掴んで設計することが重要だ。
まとめ
ここまでで基本的な梁の外力と剪断力、曲げモーメントの関係は理解していただいたと思う。
特に重要なのがしつこいが符合である。

これだけは必ず感覚として身につけるようにして欲しい。
符合を間違えると変形量を求めるときに真の値と逆になってしまい悲惨な結果が待っている。
またこれからシミレーションがどんどん増えていくが結果を判断するのは人間である。数字は誰でも読めるが符合の意味は学習しておかないと意味がわからないので危ない。
応力の引張りと圧縮のように梁も符合が変わるだけで材料に与える挙動が全く異なるのだ。
しつこく言うが流行りのAIだのシミレーションは計算するだけで答えは教えてくれない。結果を判断するのはあなた、人間である。だからこそ計算の意味、符合の意味がとても大切なのだ。
次回もかなり重要な断面の性質、断面二次モーメントについて説明する。
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。





コメント