今回は前回の熱応力での最後の案内の通り円環応力と簡単なトラスについて説明していく。
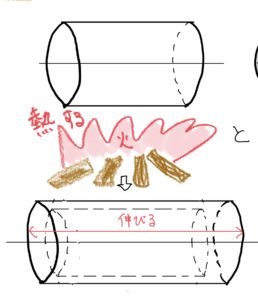
前半の円環応力は機械設計に欠かせない圧入、嵌め合いという部品同士の結合に使う代表的な手法の基礎になるので是非、理解して欲しい。
後半部のトラスに関しては、本来は曲げ応力や梁のたわみが終わってから説明するのが望ましいのだがリクエストがあったのと大学の試験でよく出るパターンがあるので解説する。
では、始めよう。
円環応力の課題設定、圧入の意味
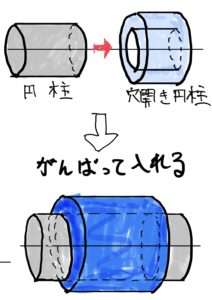
これはすごく簡単で圧入とは軸と穴の空いた円盤を用意して円盤の穴に軸を通すことである。その際に円盤の穴の径は軸の径より狭い。
つまり無理矢理、穴に軸を入れる。
そうすると多少の力では、軸は動かなく固定される。
これを圧入という。
この時の穴の径と軸の径のダブリ量を締め代と呼び、設定はJISで嵌め合い公差と言われるもので規定されている。
まあ御託は置いといて図でみてみよう。
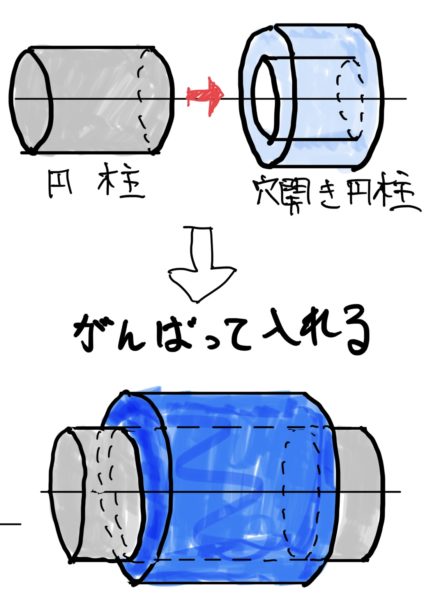
こういう感じだ。
真面目な話をすると治具を作成し円筒部品を固定してプレス機で軸を押し込むのが一般的な圧入のやり方である。
これから説明のために円環の各寸法の設定をしよう。
円環の穴とが外周の間の真ん中の半径rとし円環の肉厚はtで長さはlとしよう。この時に肉厚tは半径rに比べかなり小さい。
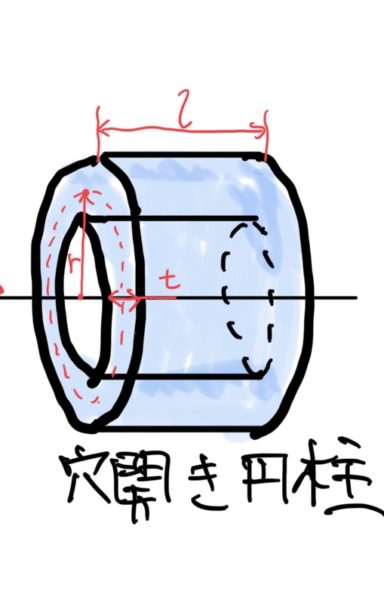
では実際に円環の応力を求めて行こう。
円環の応力
ではまず軸が圧入された場合の円環の変形を考えてみよう。
機械設計では細かい計算などに入る前に物体の動き、変形などを大まかにイメージすることは、とても大切なことなので考えるクセをつけよう。
狭い穴に太い軸を無理矢理に入れるので円環は膨らむ。膨らむ方向は、径方向と円周方向のどちらも膨らむ。長さ方向は変形しないことに注意しよう。
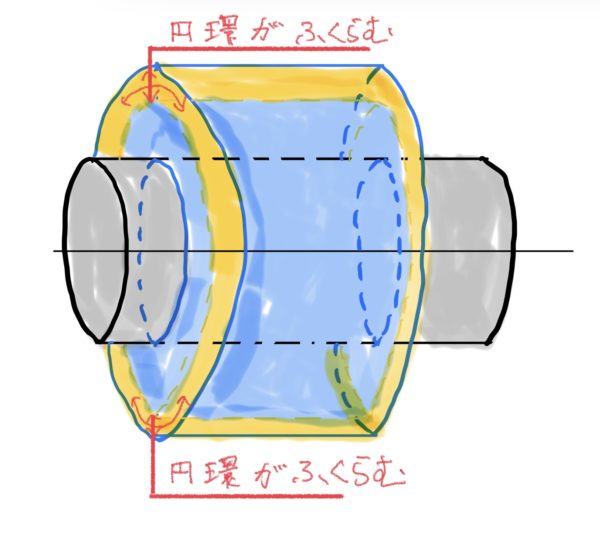
本当は軸の方に関しても潰れて圧縮されるのだが今回は円環応力の説明のために円環だけに着目する。後に別途、圧入計算という項目をつくってしっかり説明する。
変形のイメージができたところで次に円環にかかる荷重を考える。
軸は円環の穴を一様に等しく押すので円環の穴の単位面積当たり(例えば$ 1mm^2 $ごと)にq(N)かかると考えてみよう。
このような荷重を等分布荷重と呼ぶ。今回だと等分布荷重q(N/$ mm^2 $)となる。
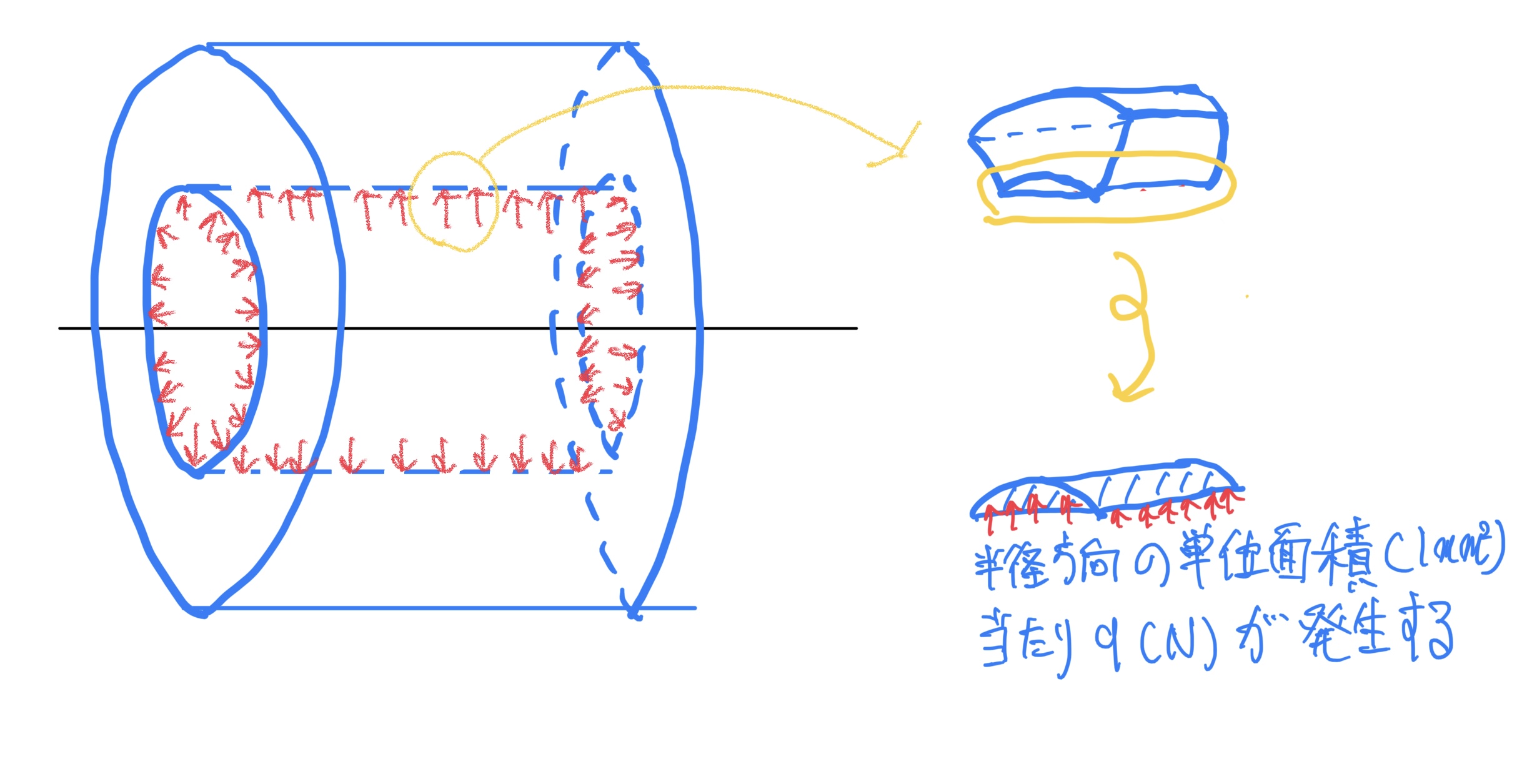
では次に力の釣り合いを考えるのが定石だが、今回みたいな荷重が広く分布していると全体を一度に考えるのは難しい。
そこでねじり応力でも使ったように一部の微小区間を切り出して考えて後に足し合わせるのだ。
では円環の一部を切り出してみよう。
まずは円環から半径rから微小角度dθ分のバウムクーヘンみたいなのを切り出す。
次にバウムクーヘンは長さがlあるので長さ1だけ切り出す。
そうすると半径rの角度dθで長さ1の超小さいバウムクーヘンができる。
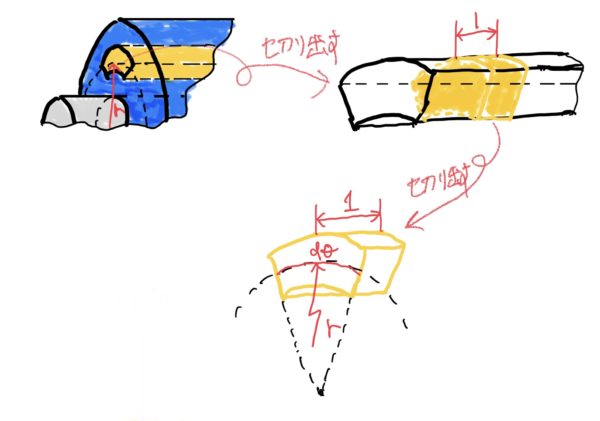
この切り取った形で力の釣り合いを考える。
まず圧入によって発生した等分布荷重qによって径方向にq×r(半径)×dθ(角度)×1(長さ)の力がかかる。
次に円周方向にも引っ張られるので円周方向の力をここでTとし考えると力の釣り合いは次の図のようになる。
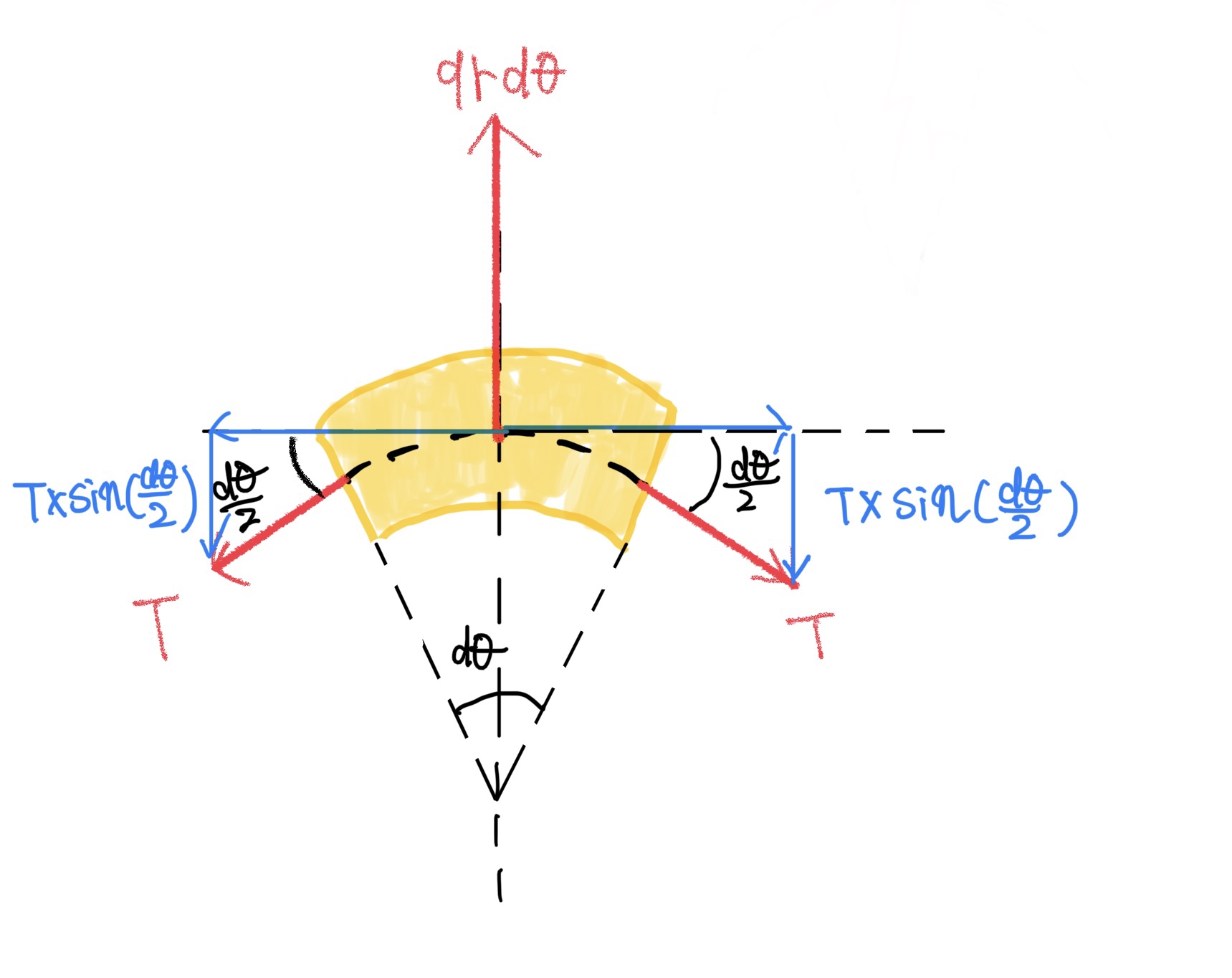
力はベクトルなのでそのままでは向きが異なって足せないので円周方向力Tを円周方向と径方向に分けると次の式が成り立つ。
$ qrdθ-2×Tsin(\frac{dθ}{2}) =0 $
ここでちょっとずるいのだが微小区間なのでdθがとても小さいので$ sin(\frac{dθ}{2})≒\frac{dθ}{2} $とする(sinは0に近いところだとy=xと見做せる)
$ T=qr $
となる。
ここまで力の釣り合いがわかったので内力である応力を考える。
力の釣り合いを見ると円周方向に引っ張られているので円周方向に引っ張り応力が発生するので次の式が成り立つ。
微小区間の断面積Aは円環の肉厚t×単位長さ1で求まる。
$ 応力σ = \frac{T}{A(断面積)}=\frac{qr}{t} $
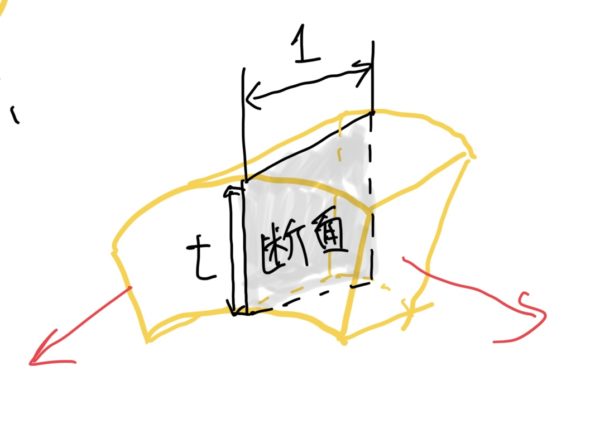
この応力をたが応力というのだが名前はどうでもよくてこの応力が円環の材料の降伏点以下でないと狙った圧入の設定で固定される力が発揮されない。
この応力が引張強度以上だと軸を入れている途中で円環が割れる。
とても重要な応力なのでよく理解しておこう。
本来では圧入の計算では軸と円環の穴の変形量をポアソン比や弾性係数を使って等分布荷重qを求める。しかしながら今回は円環応力の説明をしたいので等分布荷重qの求め方は省かせてもらった。ただし圧入計算は機械ではとても重要な項目なので別途、必ず専用ページを作成するので待って欲しい。
それはさて置き、応力が求められたので歪みも求める。
円周方向の応力なので歪みも円周歪みεと表し円環の材質の弾性係数をEとすると次の式が成り立つ。
$ 円周歪みε =\frac{σ}{E}=\frac{qr}{Et} $
また円環の変形後の平均半径をr’とすれば次の式が成り立つ。
$ 円周歪みε=\frac{2πr’-2πr}{2πr}=\frac{r’-r}{r} $
これの意味は、圧入前後で円環の寸法を計測しておけば歪みがわかり発生応力が計算できるということである。
この特性から圧入を使う場合は圧入前後で径を計測しておくと良い、というよりも絶対にしておくべきである。
以上が円環の応力、圧入の基礎の説明を終わりにする。
次にトラスの説明をする。
トラスって何だ?
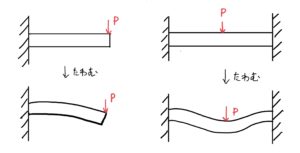
トラスとは骨組み構造のことをいうのだが次の図を見てもらった方がわかると思う。
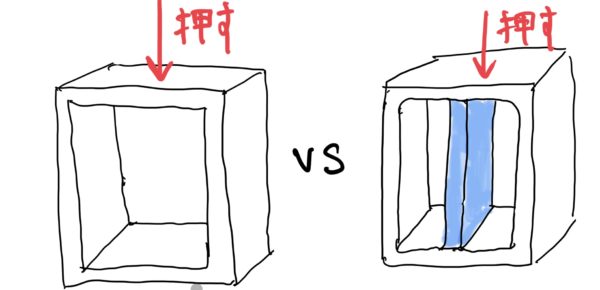
なんか箱みたいな骨組みを押すのと箱の真ん中に棒を入れるのではどちらが変形が少ないだろうか?
こんな棒みたいなのをトラスと言ったり機械設計では補強リブなんて呼ぶ。筆者の専門分野の自動車、オートバイだと昔のレーシングマシンに良く採用されていたトラスフレームが代表的だ(NASCARのトラスフレームは現役)。
では図で紹介した箱みたいなのを材料力学的に表すと次のようになる。
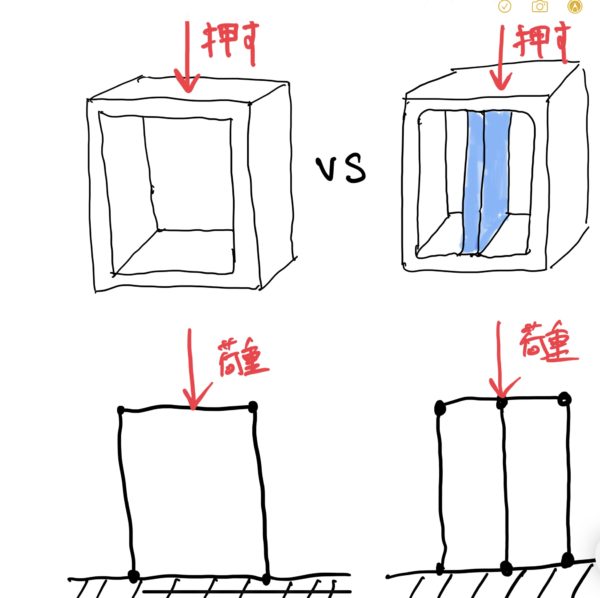
各棒と棒の繋ぎ目を節点と呼び決まった記号がある。同じ節点でも回転したり固定されたりと色々あり書き方がルールルール化されている。ただし機械設計の設計図やレイアウトでは簡略化した図を使うことがほとんどないので(全て写実に表す)さほど重要ではないと思う(建築、土木については分かりません9。
各棒にかかる荷重や応力、歪みはこれまで説明してきた知識で解を求められるが一例だけ紹介しよう。
トラスの解法例(不静定問題)
いきなり題名で見知らぬ名前、不静定問題なんて出てきたが簡単な例を解きながら説明していくので不安にならないで欲しい。
まず例題を設定する。
次の図のようなトラス構造で節点Oに荷重Pが作用する。部材AO、COの断面積をA1、弾性係数をE1とし部材BOは同様にそれぞれA2、E2とする。
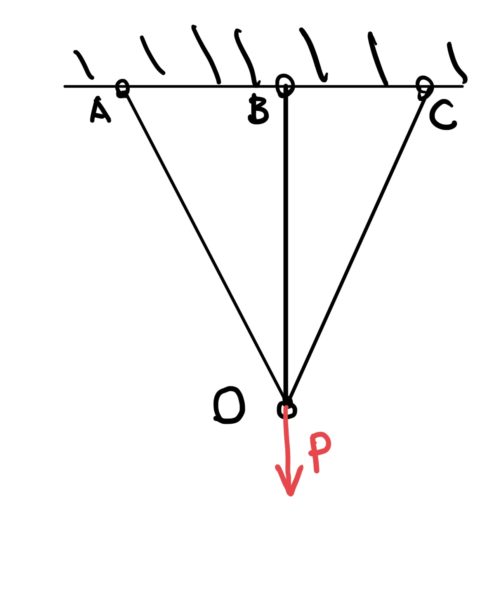
各部材の応力と変形を求めて行く。
例題はイメージできたかな?早速、解いて行こう。
いつも言っているつもりなのだがまずは変形のイメージを考えることが大切である。
式は二の次なのである。
では考えてみよう。
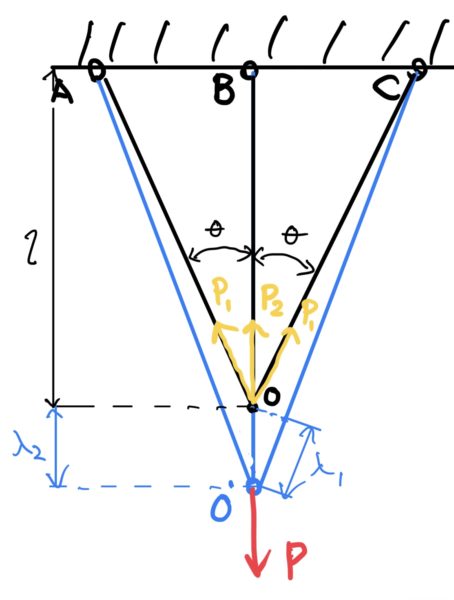
それぞれ伸びるだけである。
ここで部材AO、COに発生する引張力をP1(応力ではなく荷重)、部材BOに発生する引張力をP2とする。さらに部材AO、COの伸びをλ1とし同様にBOをλ2とする。
イメージできたらいつものようにまずは外力の釣り合いを求める。
次の鉛直方向の釣り合いの式が求まる。
$ 荷重P =P2+2P1cos(θ) $
ここから引張力P1、P2を求めたいのだが引張力は2変数に対し式は一本しかないので解けないことがわかると思う。従ってP1、P2にまつわる何らかの式をもう一つ立てる必要がある。
そこで着目するポイントは各部材の伸び量だ!
各部材の伸び量を考えて関係式を立てる(ポイント)。
$ λ1=λ2×cos(θ) $
厳密に考えると部材が伸びる前の角度θと伸びた後の角度は異なるのだが伸びが微小と考えて同じにしている。
上記のように力の釣り合い以外に物体の変形の関係式を求めないと解けない問題を不静定問題という。
基本的には外力の力の釣り合いの式を立てれば内力である応力、歪みが求まる、これを静定問題と呼ぶ(名前はどうでもいい)。
単純に力の関係だけでは解けないなとわかったら物体の変形、特に伸びの関係式を立てれば大体の場合で解ける。
慣れればすぐに静底か不静定かがわかるが最初のうちにわからないのは仕方が無い。誰だって最初はあるのだ。
例題に戻ろう。ここからは歪みから各変形量、各荷重P1、P2を求めれば良い。
まずは弾性の関係から変形量が解ける(伸び≒歪みとする)。
$ λ1=\frac{P1}{A1E1}×\frac{l}{cos(θ)} $
$ λ2=\frac{P2}{A2E2} $
これを各部材の伸び量の関係式に代入すると
$ \frac{P1l}{A1E1cos(θ)}=\frac{P2l}{A2E2}×cos(θ)、 P1=\frac{A1E1cos^2(θ)}{A2E2}×P2 $
これで力の釣り合いに代入するとP1、P2が求まる。
$ P1=\frac{Pcos^2(θ)}{(\frac{A2E2}{A1E1})+2cos^3(θ)}、P2=\frac{p}{1+2(\frac{A1E1}{A2E2})cos^3(θ)} $
ここまでくれば伸びとかは代入だけなのでここで終わりにする。
このようなトラスや応力を求めるのに静底や不静底問題とあるがさほど重要ではなく次のことを頭に入れておくことを勧める。
これで大体の問題が解けると思う。
弾性を忘れた方は、こちら。
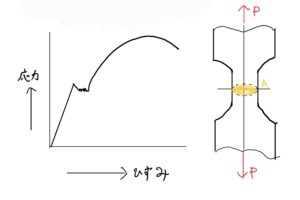
ここまで説明しておきながら機械設計において厳密解を求める力はさほど求められない。しかもコンピューターシミレーション(CAE)が発達し安価に手に入りやすいので尚更だ。
大切なことは正しい変形や外力のイメージと材料力学を理解していることである。
よって計算ができないからと落ち込まないで欲しい。意味を理解することが重要なのだ。
不静定問題
トラスの課題でいきなり不静定問題を解いてしまったがここで不静定について少し詳しく解説する。
まずは静定問題、不静定問題という言葉について説明する。
静定問題は物体に加わる外力と物体内の応力の釣り合いの式のみで応力が求められる問題のことを示す。
不静定問題は物体に加わる外力と物体内部の応力の釣り合いの式だけでは応力が求められない問題のことを示す。
なんか禅問答のような話で分かりにくいと思うので図解していこう。
下の図に似たような例題で静定問題と不静定問題を並べる。
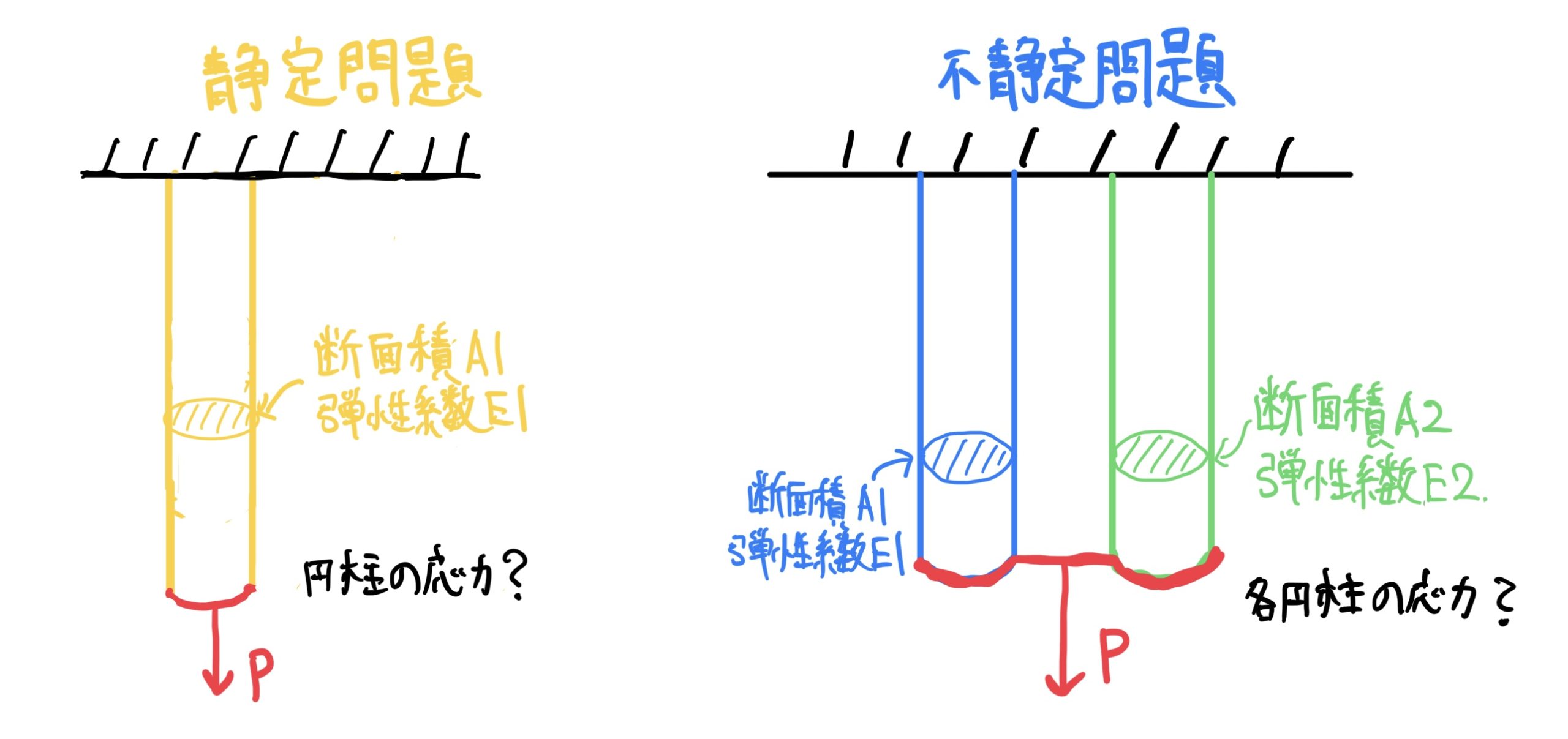
違いが良くわかると思う(不静定問題の2本の円柱はお互いがガッチリ固定されている)。
静定問題の方は簡単で断面積A1、弾性係数E1の円柱を荷重Pで引張るので応力の定義通り次のようになる。
$ 応力σ=\frac{P}{A1} $
次に不静定問題を解いていくと2本の円柱を荷重Pで引張るので各円柱には分担した荷重が掛かる。
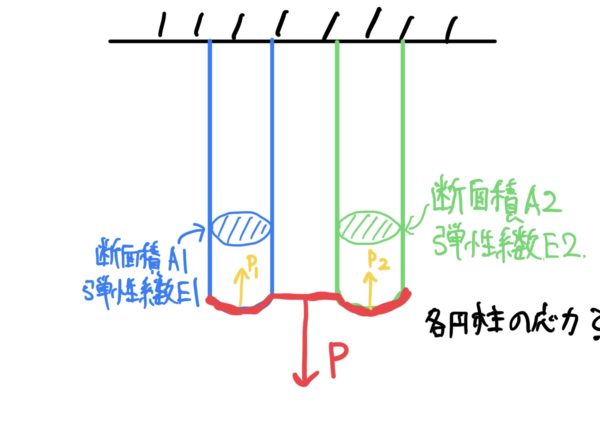
各円柱が分担する荷重は具体的にわからないので青い円柱にかかる荷重をP1、緑の円柱に掛かる荷重をP2とすると次の式が成り立つ。
$ P=P1+P2 $
当たり前だが上の式(力の釣り合い)だけでは各円柱の応力はわからない。これが不静定問題である。
ここからどうやって解いていくかというと力の式はこれ以上立てられないので円柱の伸び(ジオメトリー)で式を立てる。
2本の円柱はお互いにガッチリ固定されているので荷重Pで引いた場合の伸びは同じである(伸びをλとする)ことを式にすると次のようになる。
各円柱の伸び(伸び≒歪み)はフックの法則から
$ 青い円柱の伸び(歪み):\frac{P1}{A1E1}、 緑の円柱の伸び(歪み):\frac{P2}{A2E2} $
2本の円柱の伸びは同じなので
$ \frac{P1}{A1E1}=\frac{P2}{A2E2} $
となる。
これでP1、P2という2変数に対し式が2つ立てられたので解けるようになる(代入するだけ)。
$ 荷重P1=\frac{A2E2P}{A1E1+A2E2}、荷重P2=\frac{A1E1P}{A1E1+A2E2} $
このような流れで力の関係式以外の式が必要になるのが不静定問題だ。
算数的に考えると連立方程式で求めたい変数の数と同じ数だけ式が存在しないと解が存在しないということになるので求めたい荷重、応力の数だけ式が必要になる。必要な式が力の釣り合いだけでは満たせない場合に伸びなどの変形量(ジオメトリー)で式を補うという考え方になる。
例えば知りたい荷重がP1、P2、P3の3つだったら式が3本必要で力の釣り合いの式が1本、モーメントの釣り合いで2本で足りない分は変形量で式で3本目を成立させて解くという感じだ。
ここまでで静定、不静定について理解が深まったところで現実にはどちらの問題が多いのかを考えると筆者の経験では不静定問題が多いと思う。
筆者の感覚での見た目の違いとしては静定問題に対し不静定問題は補強するような構造物やトラスが追加されていることが多い。
言葉では分かりにくいと思うので下の図にいくつか例を紹介する。
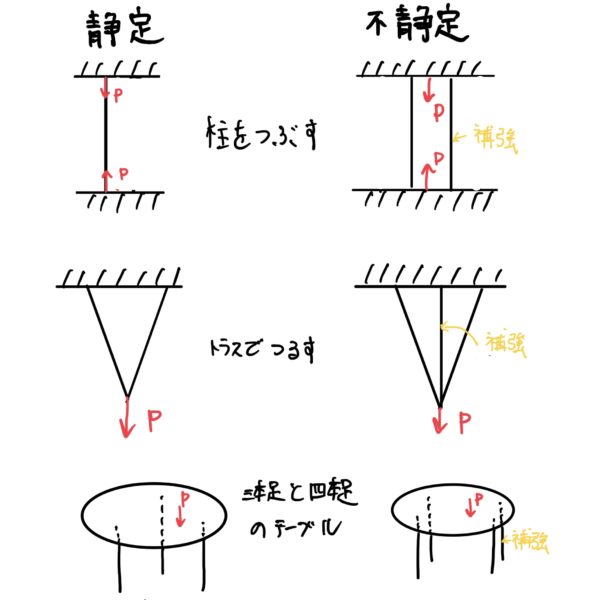
イメージが掴めただろうか?
まとめ
長くなったがまとめる。
・円環応力は機械設計で扱う圧入、嵌め合いの基礎になるので十分に理解して欲しい。
・変形のイメージは円環は膨らむこと、円周方向の応力は荷重に比例し肉厚に反比例することを理解して欲しい。
・機械設計観点では圧入の締め代が大きくて円環の肉厚が小さいと円環が割れるか塑性変形して使い物にならない。
・圧入前後で寸法は必ず押さえておくこと。後から測ろうとしても圧入してしまったらもう終わりだ。筆者は何度も痛い目に会っている。
トラスに関して今回は触りだけなのでまとめは省略する。
次回はようやく梁(はり)の解説に入る。
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。






コメント