前回の解説でRAEの再現テストでコメット墜落事故の仮説が検証された。
軽くおさらいをすると仮説は“与圧室の窓の角やアンテナの取り付け穴に応力集中が発生し、破壊が進展していって疲労破壊が発生し空中分解した“であった。
RAE(イギリス王立航空研究所)再現テストの結果は、1000万回の繰り返し荷重を想定するのに加え開発、製造会社の見積もりも5万4000回に対して実際の事故とRAEの疲労試験結果は3000回未満とで破損と桁が違うレベルなので何が起きていても不思議でないくらい危ないことがわかった。
これにより仮説は、実証されてコメットの墜落事故の原因が判明した。
今回は、コメットの墜落事故の原因である応力集中と疲労破壊の解説を中心に進めていく。
まずは、応力集中とは何か具体的に解説していく。
応力集中
コメットの墜落事故の大きな要因の一つである応力集中を説明していこう。
応力集中といきなり言われてもなんのこっちゃと思われるかもしれないので概要だけ簡単に説明する。
応力集中とは部材の断面の形状が急激に寸法変化(形状変化)をしていると,そこに力が集中することだ。
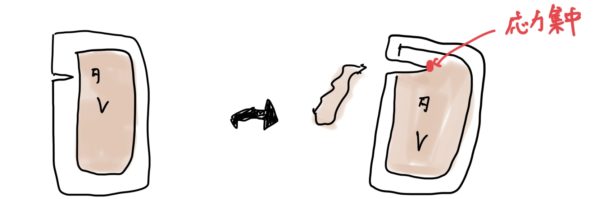
簡単に言うと生活の中で体験できる応力集中は、納豆とかフランクフルトなどを買うとほとんどの場合で個装のタレやケチャップがついてくると思う。
そのタレやケチャップを個装から取り出すときに包装の切れ目が入っている部分を手で切って取り出すはずだ。
簡単に切れるのは実は、その切れ目が急激な形状変化となって小さな力でも応力が集中して大きな力となり包装が破壊されることによって中身が取り出せる。
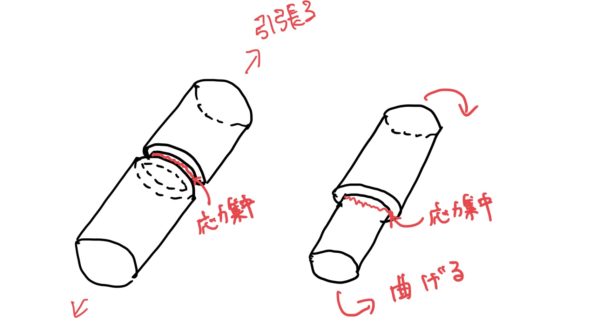
他にも経験したことがあると思うが段付き棒であれば段差のところから壊れたり溝がついた棒が溝の部分から壊れるのも応力集中が原因だ。
この応力集中は古代から知られており機械においては、応力集中を避ける工夫を必ずしている。
それでも設計上でどうしても応力集中する部位は出てくるので、その時は力の集中の度合いを最小限に抑える工夫をしている。
応力集中の詳細は、こちら
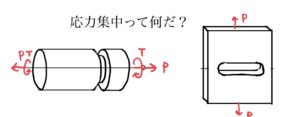
当然、コメットにもこの応力集中が発生していた。
その代表的な場所は、前回の仮説で出てきた通り窓の角に応力集中していた。
当然ながら窓の角のようなところに応力が集中するのが開発、製造会社でも解っていたので窓の角に丸みをつけて対応していたのだがそれでも工夫が足りなかったようだ。
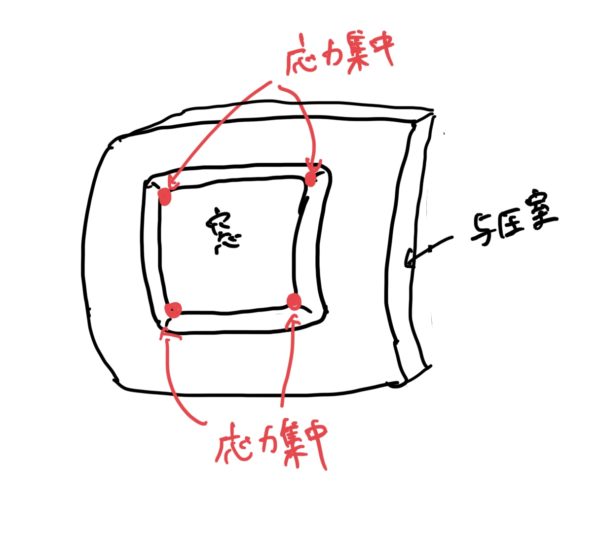
結果論になってしまうが窓の角の丸みが足りなかったことによる応力集中が発生していたのである。
次の大きなポイントが疲労破壊だ。
疲労破壊
ポイントが繰り返し荷重による疲労破壊である。
疲労破壊を簡単に説明するとあらゆる材料、部材は破壊される強度以下で使用しても繰り返し荷重を加えるとある一定回数で破壊されるのだ。
身近な例だと針金が代表的で針金をグニグニ曲げているとある回数のところで針金が折れる経験をしたことがあると思う。
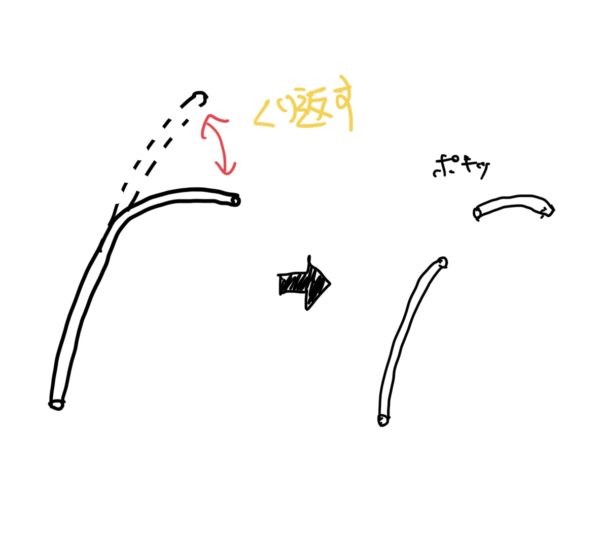
またプラスチックなんかでも繰り返し使っていると折れたりするのは、生活で良くある現象だと思う。
これを疲労破壊と呼んでいる。
この疲労破壊は、どんな材料を使っても発生するのでどのくらいの荷重が繰り返しをどのくらいの回数加えると壊れるのか材料ごとに指標があるのだ。
機械設計では途方もない数字だが$ 10^7 $回以上耐えられる荷重、応力を疲労限と呼び、これを利用して機械が寿命を迎えるまで持つように設計している。
逆に、この疲労破壊の回数を基に機械の寿命やメンテンス期間を決めているのだ。
疲労破壊の詳細は、こちら

当然、これも以前から知られておりコメットも開発、製造会社では考慮して設計し耐久試験まで行っている。
それでも結果論だが、設計での検討や耐久試験が十分でなかったようだ。
結果、この二つが主な要因となり当然ながら飛行毎に離陸ー飛行ー着陸を繰り返すので高度差による気圧変動の繰り返し荷重が与圧室に発生し、窓の角とアンテナの穴に応力集中が発生したことにより疲労破壊し空中分解して墜落したのだ。
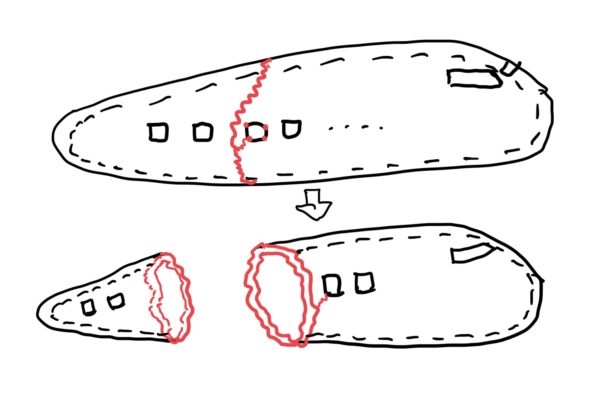
では、ここで誰もが疑問に思うのが“開発時にしっかりと耐久テストを行っていたのに何故、与圧室は疲労破壊したのか?“と“開発時のテストでは疲労破壊が発生しなかったのRAEのテストでは何故、疲労破壊が発生したのか?“になる。
この疑問を解明するために両者の耐久テストの違いを見ていこう。
開発時の疲労テストとRAEの再現テストの違い
まず開発時のテストの方法とRAEの再現テストの違いを挙げていく。
まずは、おさらいになるがRAEの再現テストでは機体を丸ごとプールに入れて水の出し入れで気圧差による繰り返し荷重を再現していた。
さらにプールの水を抜いて機体内部に水を入れることで高高度時の機体の膨張も再現していた。
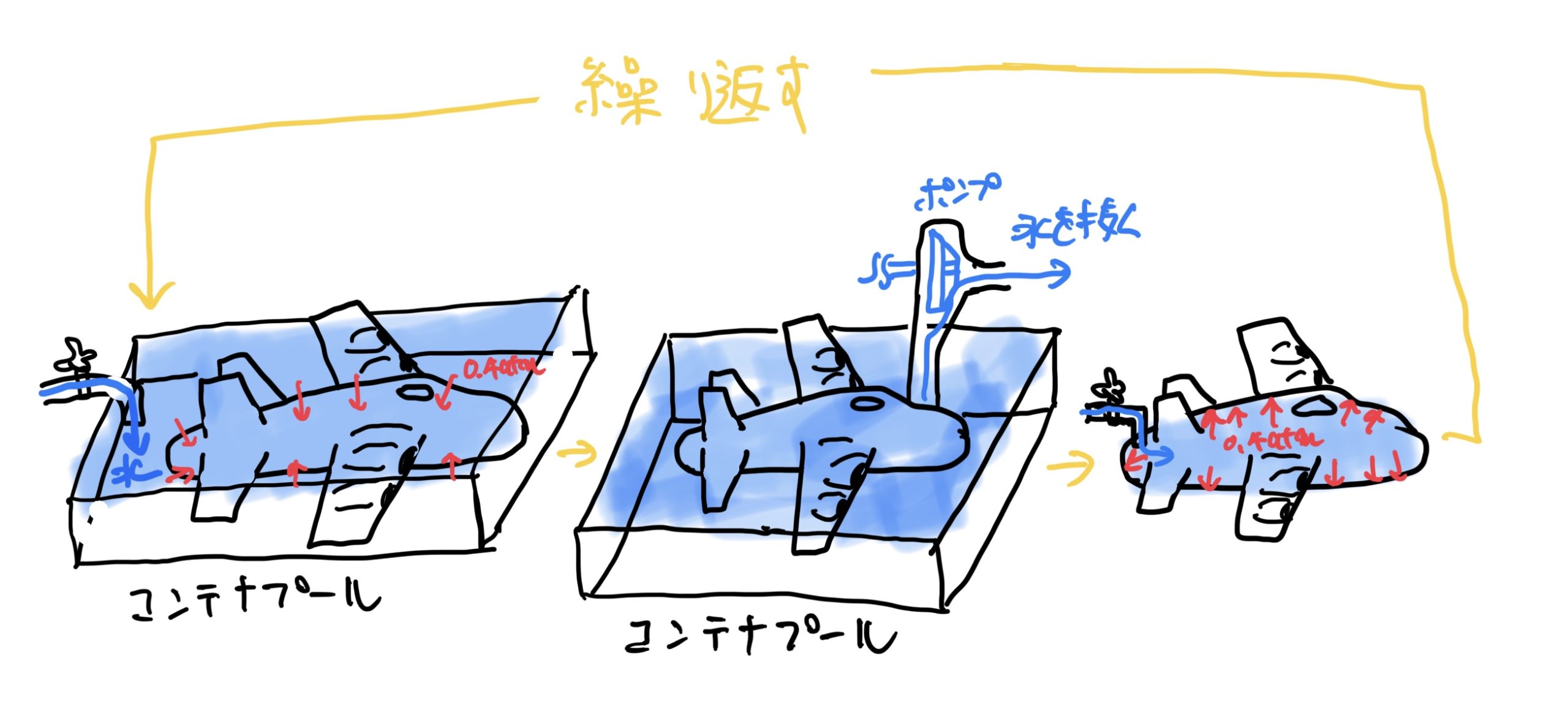
これを繰り返すことにより飛行毎の負荷を再現していた。
では、一方で開発、製造会社はどのような試験を行っていたのかを見ていこう。
試験の状態を箇条書きで書くと次のようになる。
1、機体が丸ごと入る試験の施設がなかったので与圧室を分割して耐久試験を行った(分割して部品をつくり接着して与圧室を作っていたのも大きな理由の一つ)。
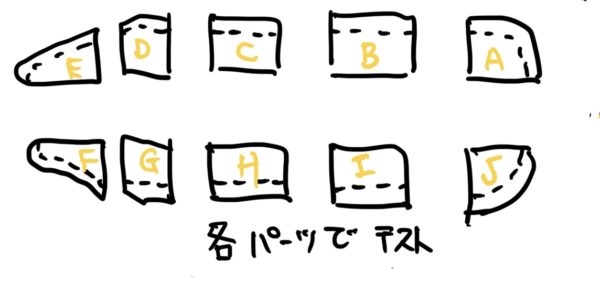
2、分割されている与圧室がどのくらいの負荷で壊れるのか(一発破壊)を調べるのに飛行で掛かる荷重の2倍の荷重を与える試験を行った。
3、2の試験で使用した分割されている与圧室を使って繰り返し荷重を掛けて疲労試験を行った。
4、疲労試験の内容が気圧差による荷重、圧力0.6atm(60kPa)を繰り返しかけるのだが念のため1000回毎に2倍の1.2atm(120kPa)を与えていた。
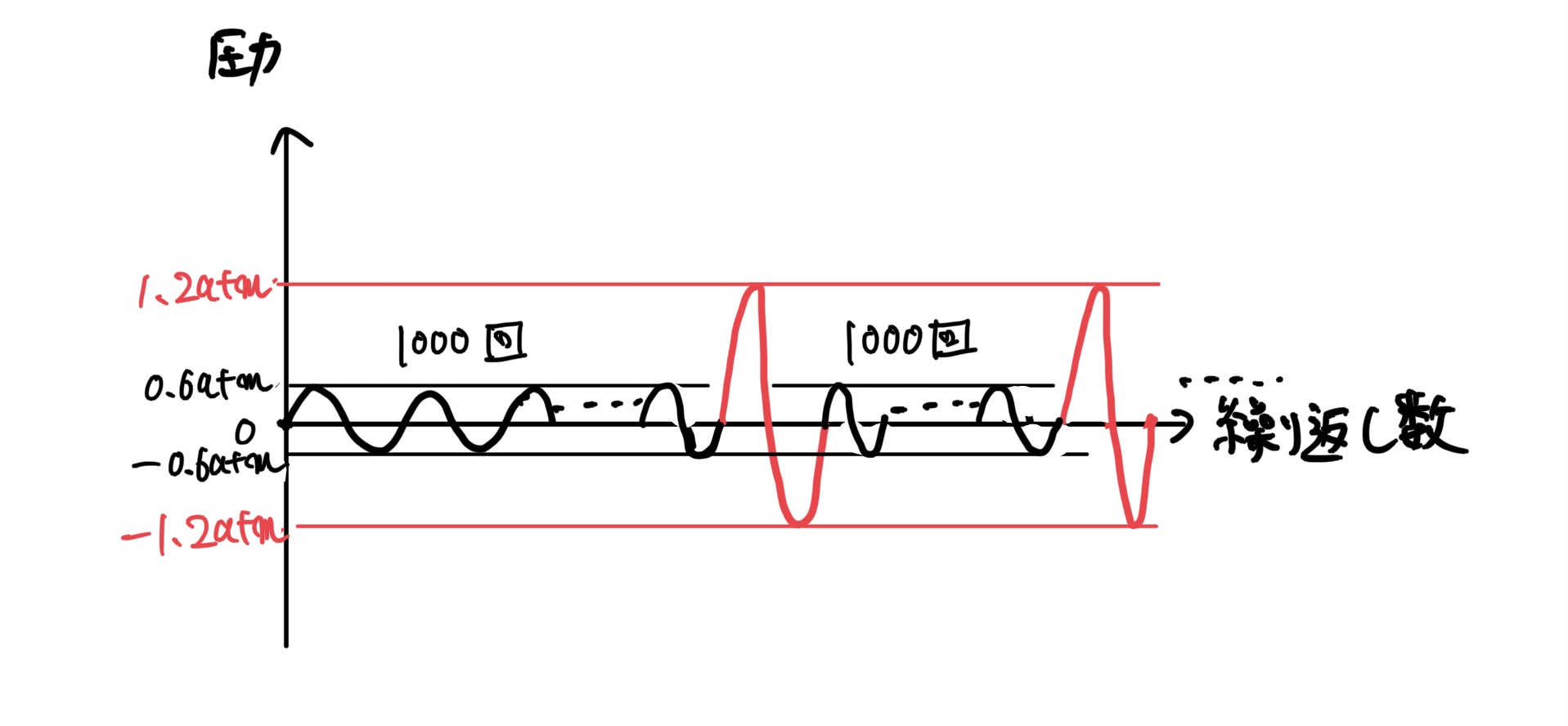
5、繰り返し荷重を与圧室に与えるのに圧縮空気を利用して与圧室に繰り返し荷重を与えた。
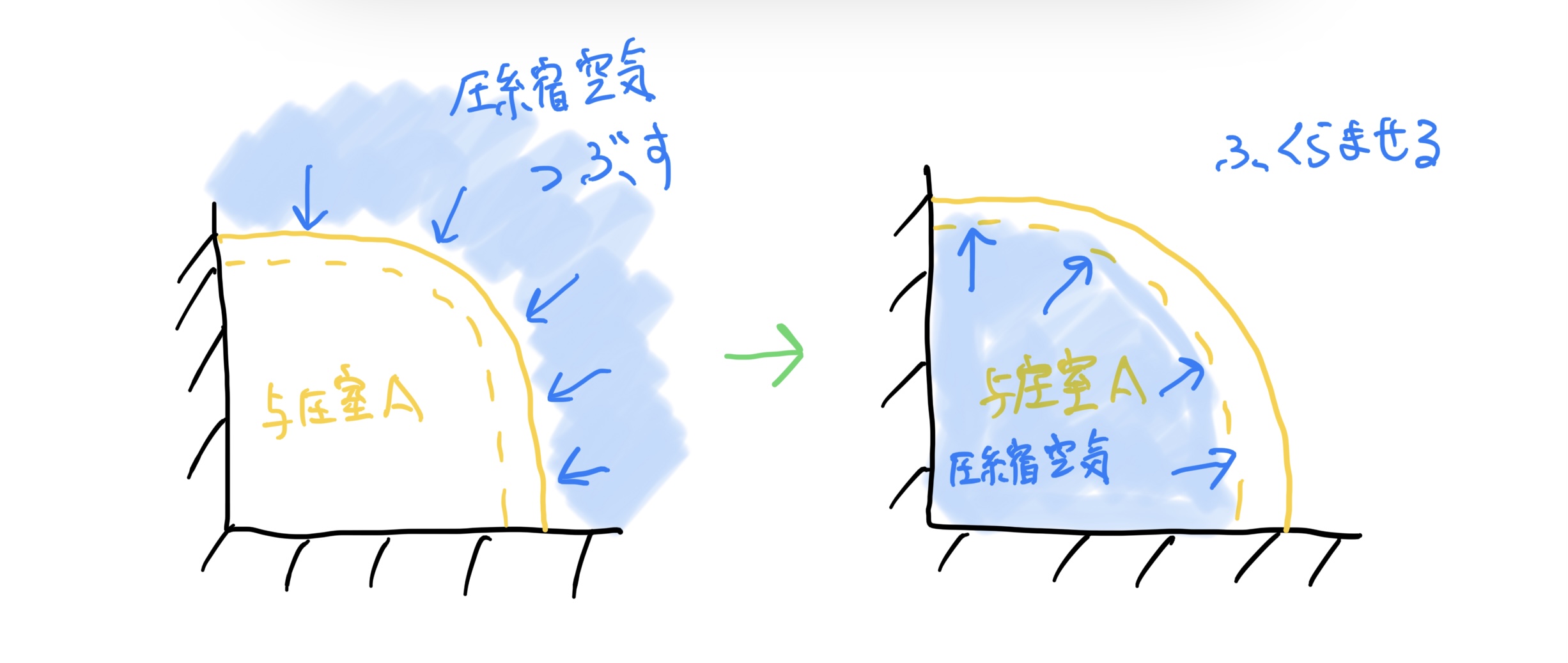
パッと見ると開発、製造会社の試験内容は、問題ないように見える。さらに世界初なので念のために機体に掛かる荷重の2倍の荷重を与えて確認しているのだ。
これだけだとRAEでの再現テストより厳しいテストを実施したように見えるが大きな落とし穴があったのである。
この試験内容の差がコメットの試験結果にどんな差を生み出してしまったのかメカニズムを見ていこう。
与圧室を分割して試験を行った影響(有限要素法)
ここから少しだけ専門的になるのだが面白い内容だと思うので、なるだけ誰でもわかるように丁寧に説明していく。
まず最初の大きな落とし穴は分割した与圧室での試験と機体を丸ごと使って試験(RAE)を実施した差である。
開発で分割した与圧室で試験をする事自体は、間違いでも悪いことでもなく巨大な部品を試験をする場合に現代でもよく使う手法の一つだ。
ただし、しっかりと試験の条件を考えないと分割した部品と完成した部品で挙動が全く異なるのだ。
まずは、簡単なはりを例にして分割した場合と丸ごと試験した場合にどんな差が出るのかを紹介しよう。
単純なはり(壁に設置したつっぱり棒)の変形
まずは、両側で固定されている長さlのはり(つっぱり棒)を考える。そこに等分布荷重q[N/m](圧力と考えても良い)が一様にかかっている。
普通に考えれば次のように変形するのが想像できると思う。
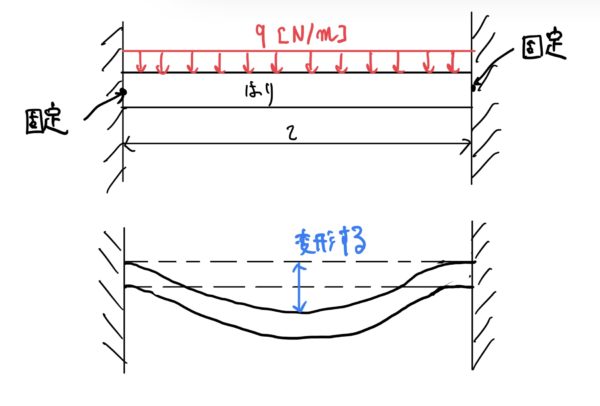
ちょっとイメージしづらい場合は、身近な例で考えると100均やホームセンターで販売されているつっぱり棒を考えよう。
そのつっぱり棒を壁に設置して濡れた超重い布団を棒の長さ一杯に2つ折りにして干すと例題と同じような条件になる。
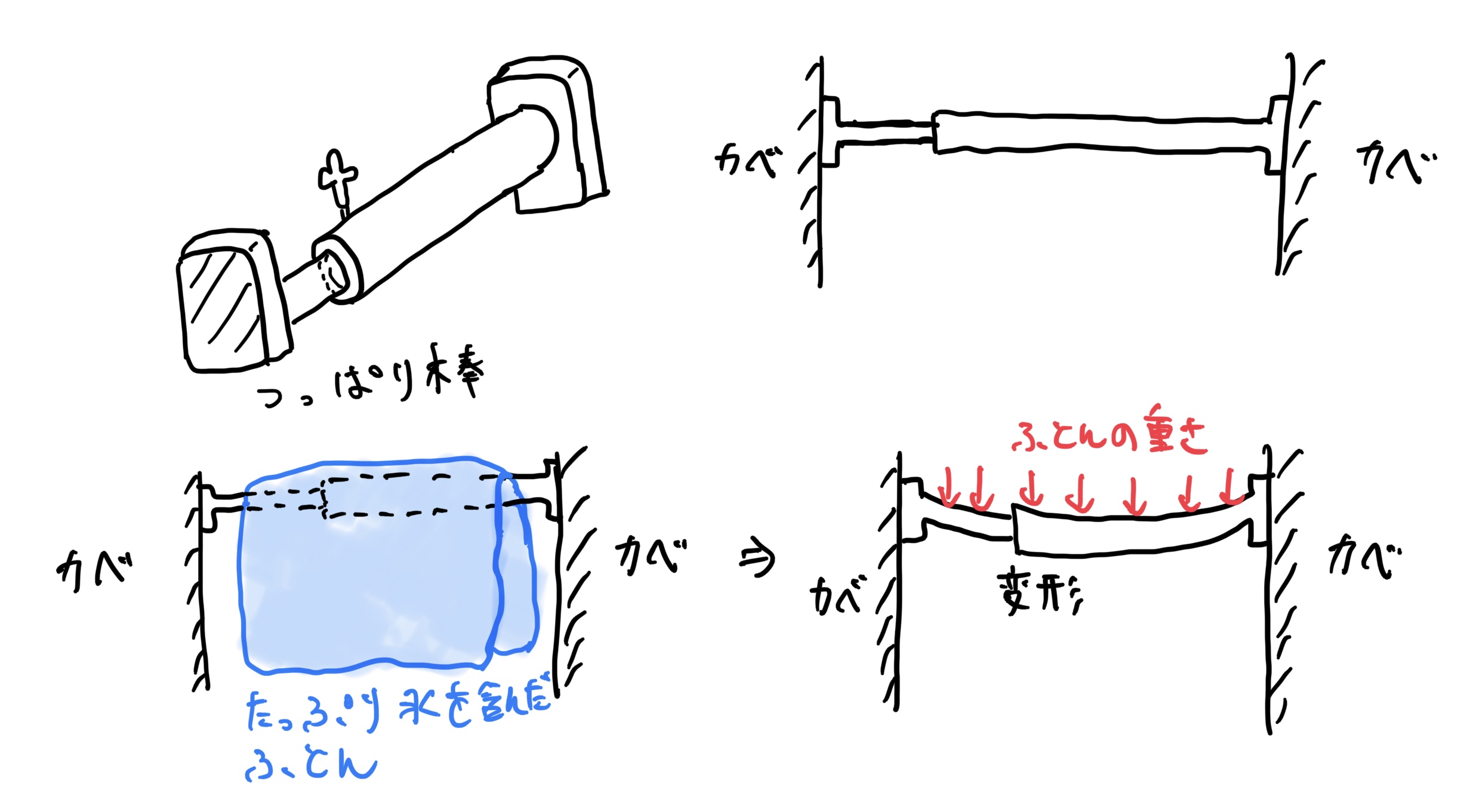
では、分割して考える場合の手法を紹介しよう。
単純なはりの変形を分割して考える
まずは、真ん中の長さ$ \frac{l}{2} $の位置で分割してみる。
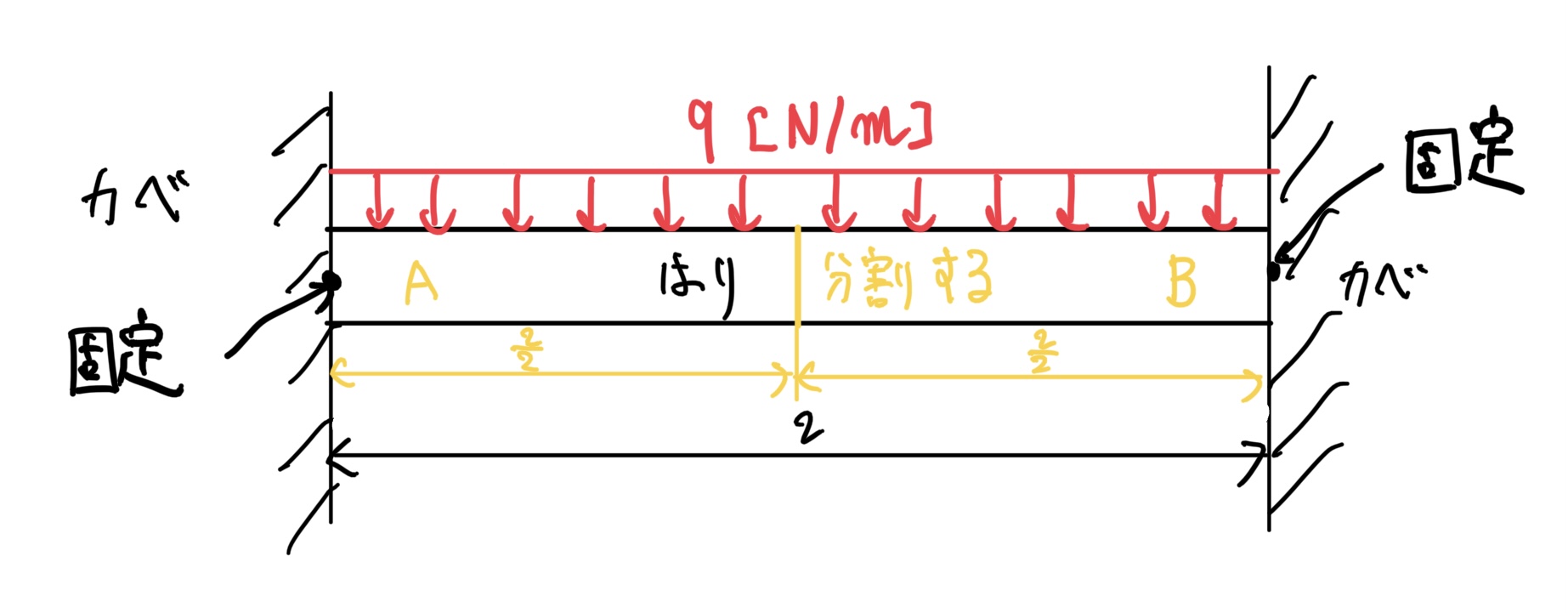
そうすると分割したA、Bは次の図のように考えられる。A、B共に片側が固定された棒で分割する。
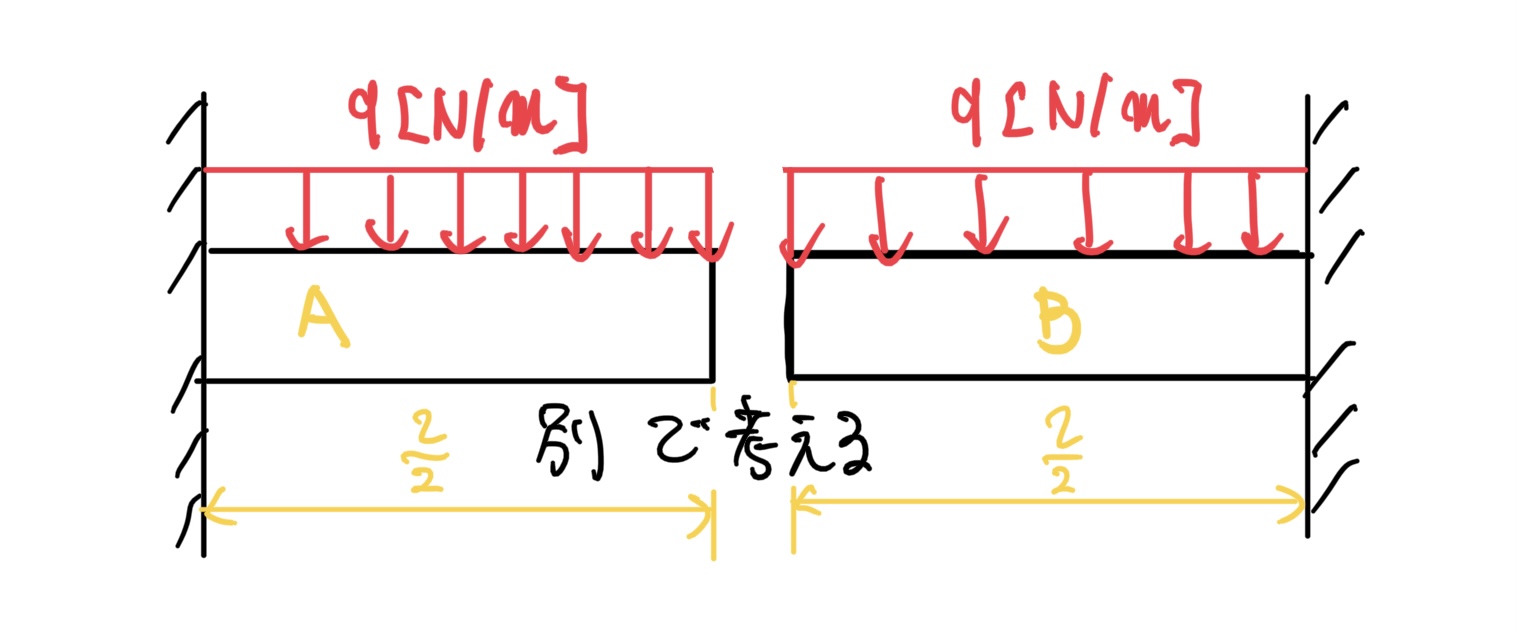
これらA、Bの変形は、簡単で次の図のようにたわむ。
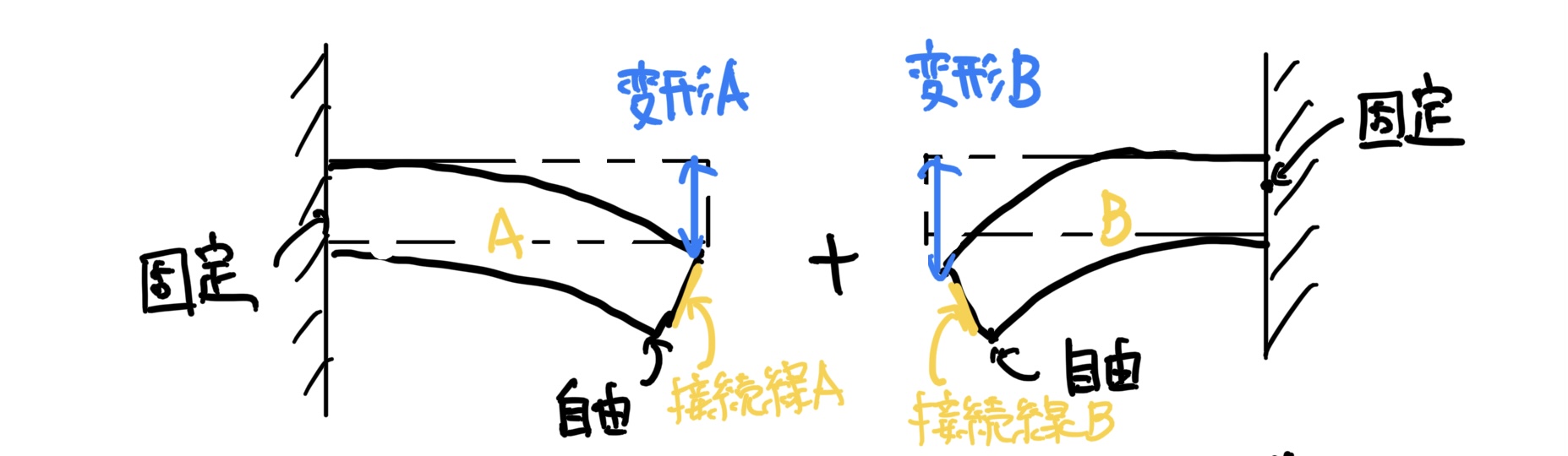
布団で考えると次のようになる。
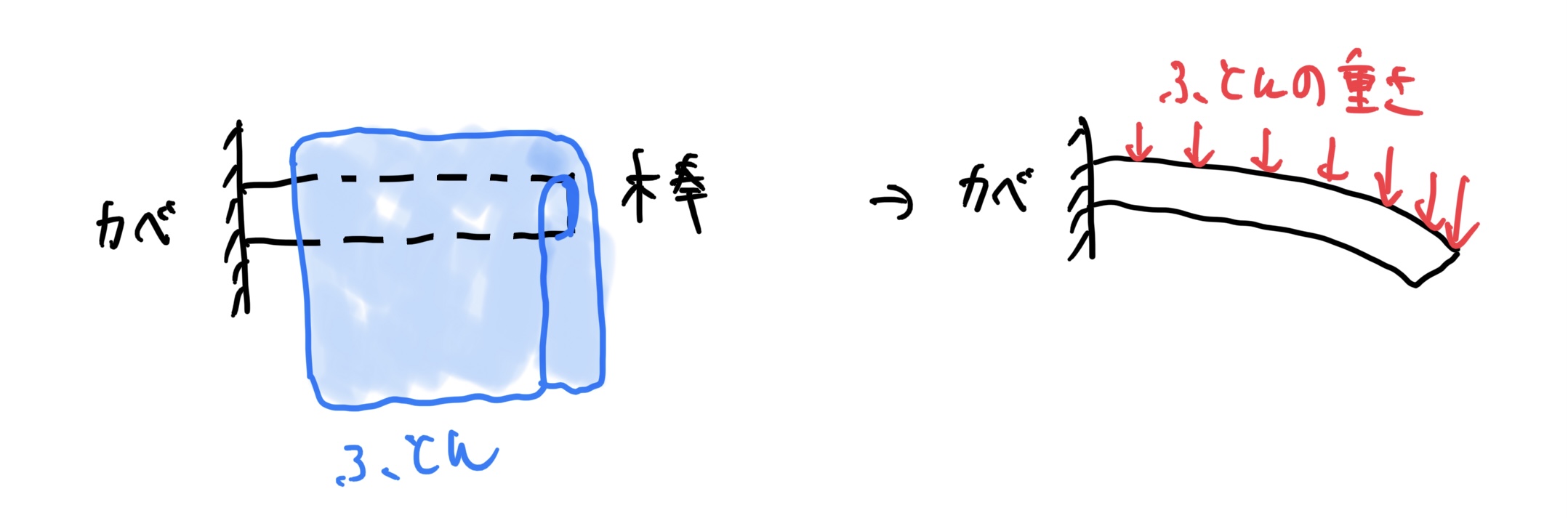
これを元の形に戻すために合体するのだ。
この時にA、Bは連続して繋がっているので接触面A、Bの変形量は等しくなることに注意だ。
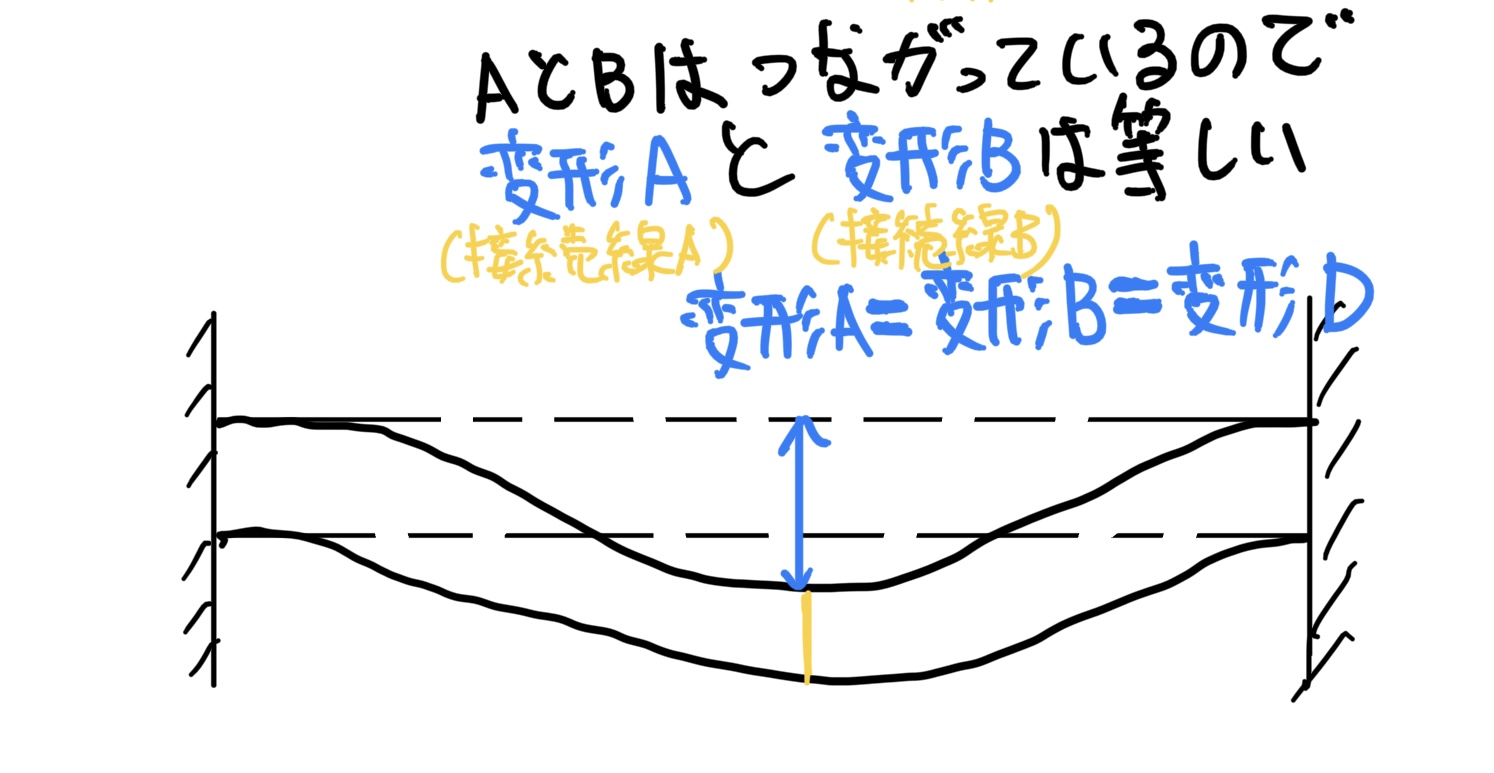
そうすると元のはりの変形と同じ結果になるのだ。
まあ、この例だと簡単なのであまり分割して計算する意味はないが、形状が複雑な場合に簡単な形状で分割して、それぞれを計算して合体すると簡単に元の形状の変形が求められる。
ただし計算は簡単になるが、計算量は増加する。
このように分割して計算やテストをする方法を有限要素法(FEM:Finite Element Method)と呼ぶ。
これは現代のありとあらゆるコンピューターシミレーション(CAE)の基本的な仕組みで超複雑な形状を何千、何万個の要素に分割して計算するのだ。
コンピューターは単純な計算を超高速で複数回、実行するのが得意な機械なので相性がとても良いのだ。
執筆時点で皆さんが見たことがあると思われるのは、コロナ関連でスーパーコンピューター富嶽を使って計算した“室内で人がくしゃみをした時の唾の飛沫の飛び方“のシミレーション結果の動画をニュースかなんかで見たことがあると思う。
あれは、流体の解析だったり時間を分割して計算していて弱冠、複雑なのだが原理は、ここで紹介したのと全く同じなのである。
ただ、分割の方法を間違えると結果が全く異なるのだ。
分割を間違えた単純なはりの変形
例えば、さっきのはりを同じように分割したとしよう。
ただし今度はA、B共に両側固定のはり(つっぱり棒)として分割する。
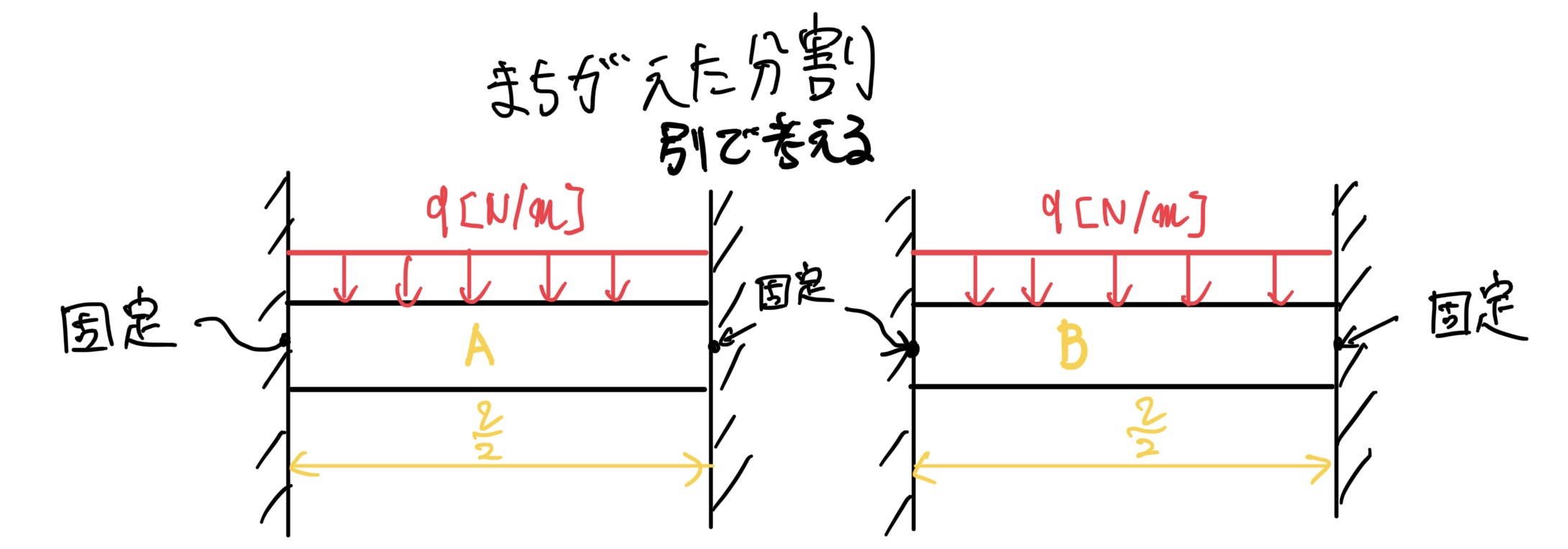
この分割したはりの変形をそれぞれ考えると次のようになる。
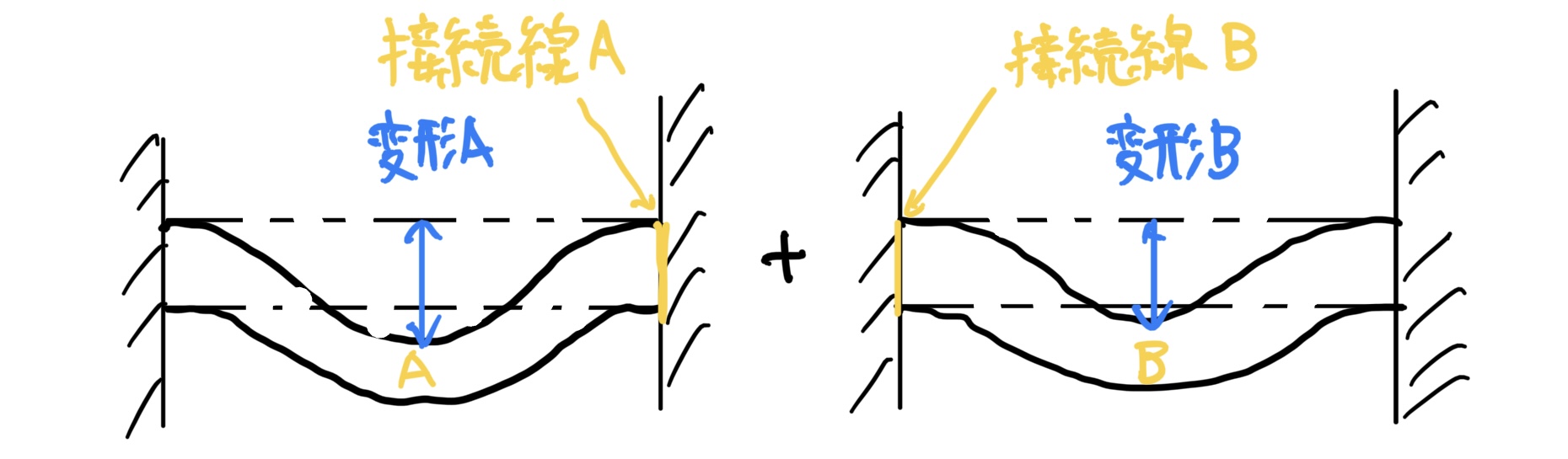
さっきと同じように元の形に合体する。この時にA、Bは連続して繋がっているので接触面A、Bの変形量は等しくなるよね。
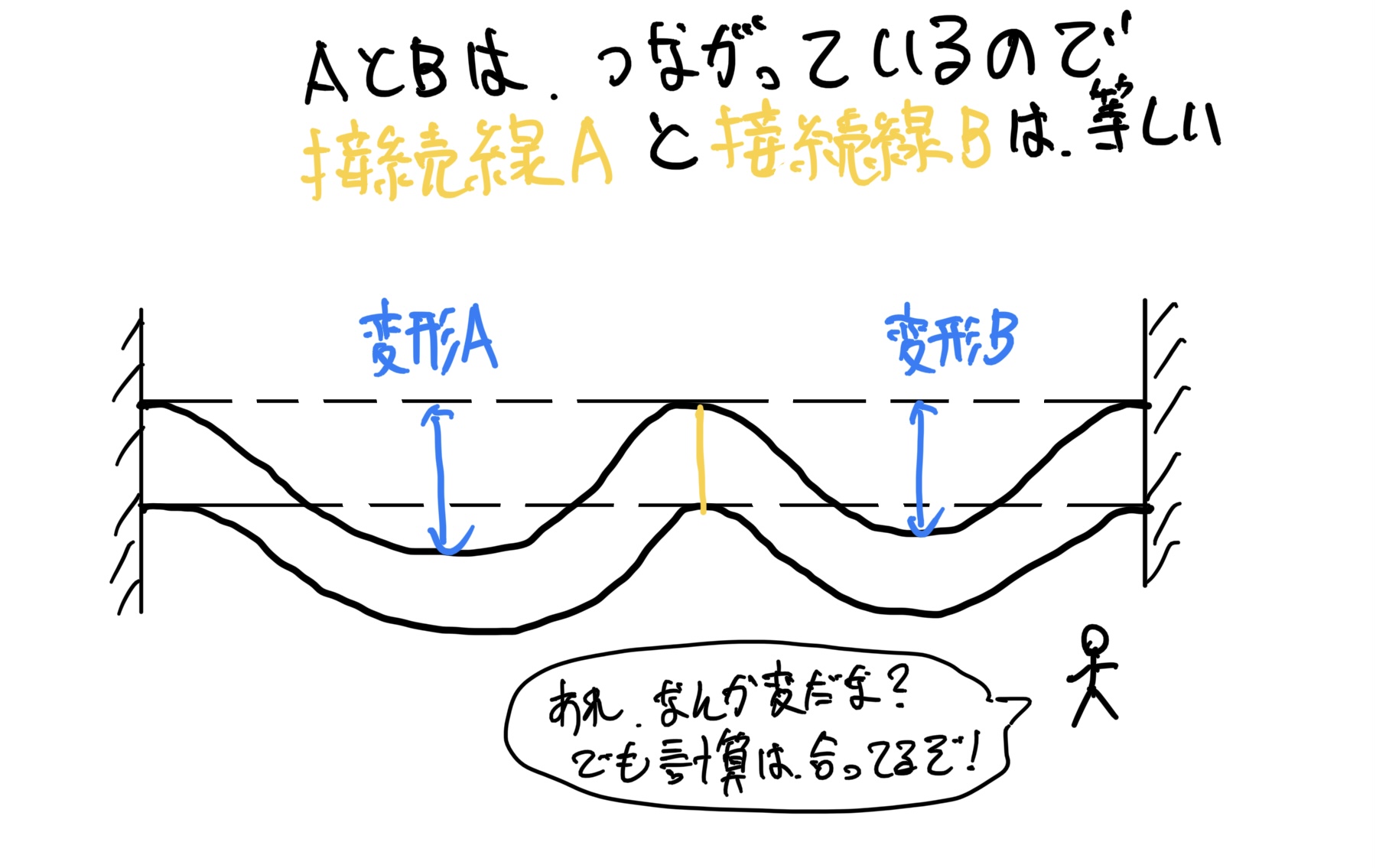
これは、誰でもわかると思うが絶対にこんな変形はしないよね。
濡れた布団を干してもつっぱり棒は、Wのカタチには変形しない。
でも計算自体は全て合っている。
間違いは唯一、分割した時の分割線の条件が自由か固定だけを間違えているだけだ。
たった一つのミスがこれだけの結果の違いを生み出すのだ。
この分割した時と合体する時の条件を境界条件(Boundary Condition)と呼び超重要な項目なのだ。
今回は、単純なはり(棒)だから誰でもこんなの間違えていると気づけるのだが超複雑な形状を何千、何万個にも分割した計算だと気づくのがかなり難しい。
つまり間違えていることに全く気付かないのだ。
じゃあ、どうやって正しい境界条件なのかを調べるのは、結局のところ最後は実機で測定するしかないのだ。
結果の正しさを判断するのは、今も昔も変わらずに地道な試験、実験の積み重ねと人間の判断力に掛かっているのだ、超重要なのである(今のAIでは、判断できない。将来は、わからんけど)。
ただし、この境界条件さえわかってしまえば次回から同じような現象であればシミレーションや分割したテストでも正しい結果がわかるので早く正確に答えがわかるのだ。
実は、この“分割方法や境界条件のノウハウをどれだけ持っているか“が経済では見えない企業の実力なのだ(いつものやつ3回目かな?)。
だからコロナ関連でシミレーション結果の動画だけ見せられても実際の現象と合ってるのか、間違えてるのか全く判断できない。
この分割方法と境界条件を教えてくれないとわからないのだ。
だからあのくしゃみの動画だけだと“大変な計算をしたんだな“くらいしかわからないのだ。
誰かが自分の金で趣味で実施するなら全く問題ないのだが貴重な税金と時間を使って動画だけ見せられてもはっきり言って困るのである。
しかも評判が良かったのかどうかわからないのだが電車の中、オフィスの室内などの異なる条件でのシミレーションばっかりやっている。
まともなエンジニアなら異なる条件のシミレーションの前に最初に計算したシミレーションと実際の現象との相関を取るテストを実施するのが普通である(仮説と検証がセットであることと同じ)。
実際の現象と相関をとっていないシミレーション結果はただの想像に過ぎず、遊んでいるのと変わらないのである。
それはさておき、これが分割方法と各分割部分の接続条件を間違えたことによる試験結果の差(シミレーションも同じ)になるのだ。
では、コメットではどんな分割方法の間違いが起きたのか極端で単純な例で示す。
コメットの分割した試験の誤った結果の例
まずコメットの与圧室は、巨大なので分割して部品を製作して最後に接着剤でくっつけて完成させていた。
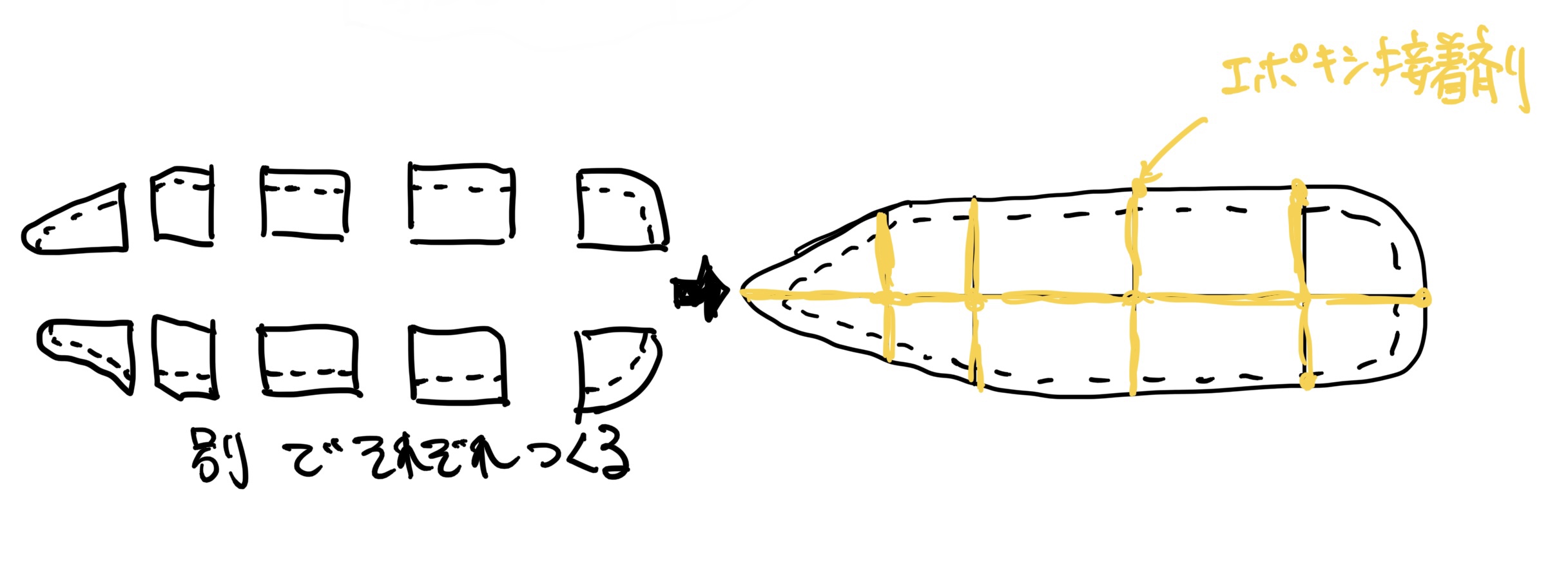
おそらくこの分割してつくったのが幸いして(結果的には、不幸だったが)そのまま分割したままテストをしたことは、間違い無いと思う。
じゃあ接着剤で完成させる前に試験をしておこうとなる。
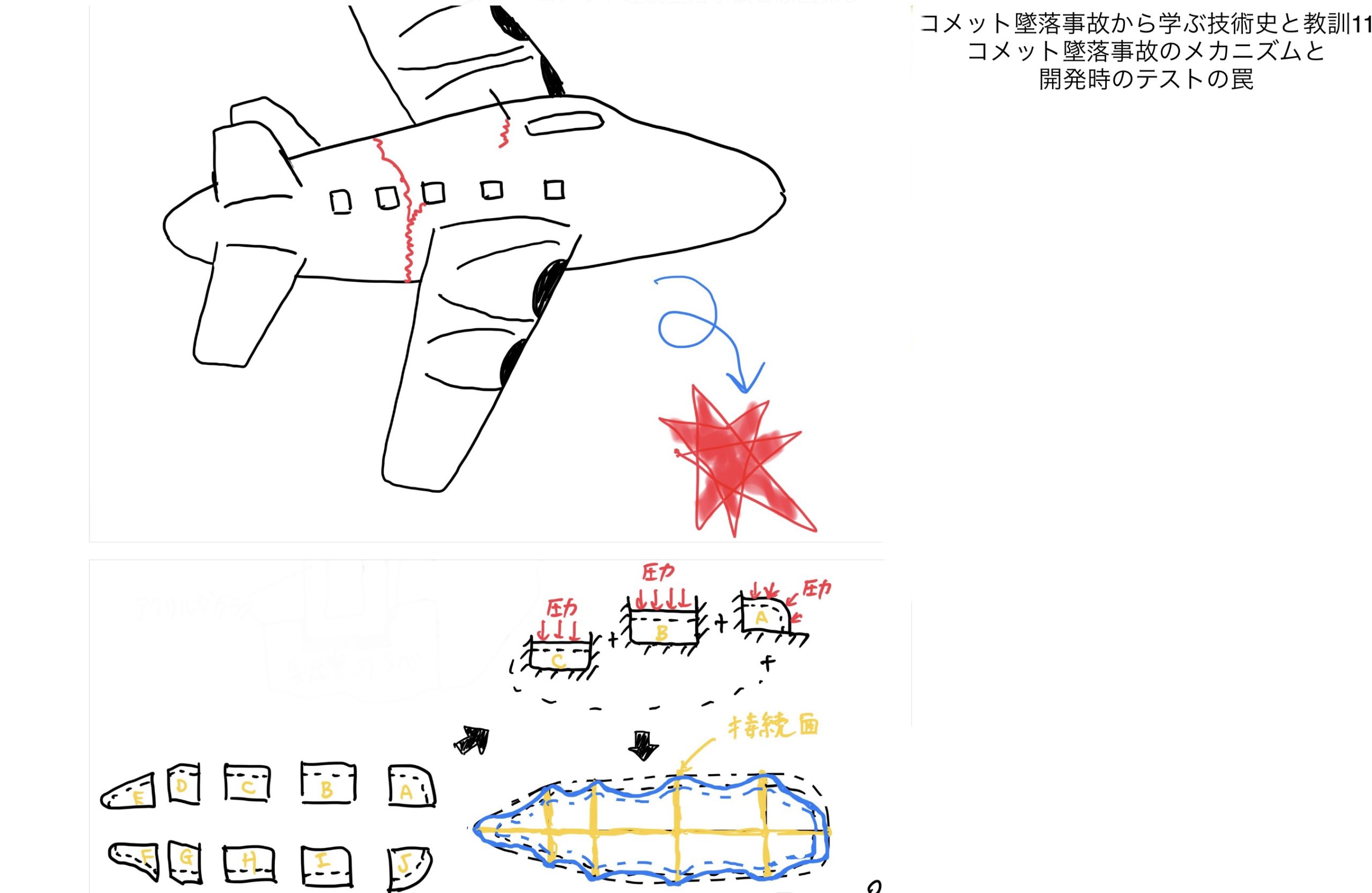
単純に各部品を固定して試験をする.
各部品の試験結果を単純に足し合わせると次の図のように与圧室は変形することになてしまう。
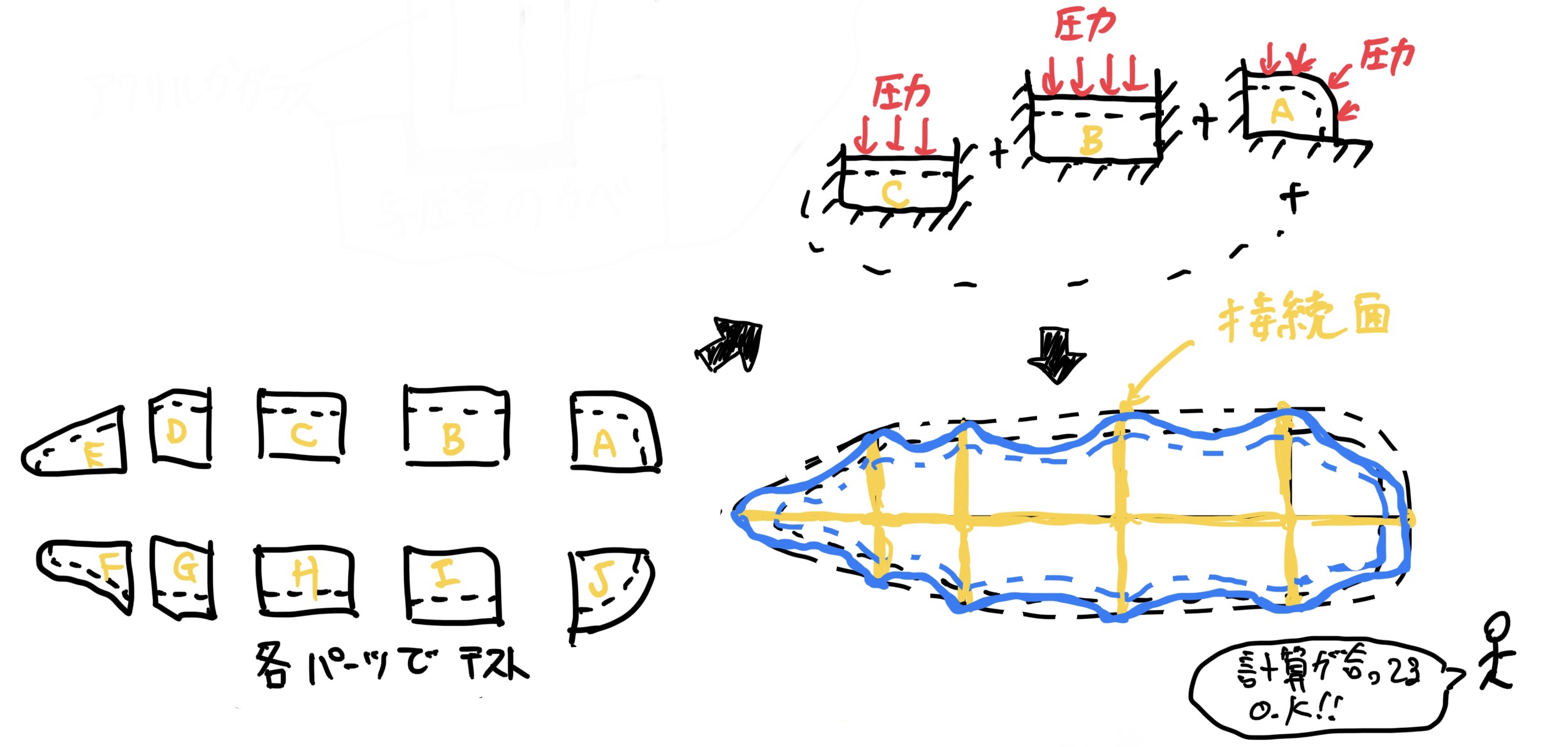
これだと絶対に間違えてるよね。この間違えだと各分割面(接合面)は、全く変形しないことになってしまうのだ。
でも当時は、与圧室全体を試験する施設もないしコンピューターもないので確認が難しい。
しかもどこかの境界条件を間違えているだけで計算自体は、合っているから全体の間違いに気付きにくいのだ。
図の例だと、たかが10部品だけの分割だが実際は、もっと分割していたと思うのでその分だけ境界条件も増える。その多くの境界条件を一つでも間違えると全体がおかしくなるのだ。
どんな天才でも人は、ミスをすることを基に考えてチェックをしないと大変なことになるのだ。
身近に潜む有限要素法の罠
先ほど現代の例で述べたコロナ関連のくしゃみのシミレーションもこのようなミスを内包している可能性が高い。
なぜならば筆者が調べる限りだと境界条件や分割方法の具体的なデータが見つからないし、どんな実験と合わせこみをしたのかわからないのだ(ちゃんと実験してる?)。
はっきりって筆者ですら、スーパーコンピューターとソフトと時間があれば、あのくしゃみのシミレーション計算と動画をつくるのは、さほど難しくない、かなりめんどくさいけど(エンジン内の油の飛沫とか燃料の混ざり方とかを計算していた)。
ただ“実際の現象とどうやって合わせるのか“が超難しいのだ(分割方法や境界条件の合わせこみ、現実との相関)。
そもそも“くしゃみの何を測定するのか“から始まるのだ(測定が超大切)。
でも動画だけを見せられると最もらしいように見えて、それを基に国家や自治体がいくつかの対策などを実施してしまうのだ。
その結果、場合によっては何の意味もない対策をして国民の労力と税金と時間の無駄になってしまう。
しかも日本のトップレベルの頭脳が集まる理化学研究所が自慢げに発表しているからタチが悪い。
このシミレーションと実際の現象の差は、シミレーション(CAE)が流行り始めた10年前から多くの企業内で多発し続けているのだ。
何も筆者は、“くしゃみのようなシミレーションを無駄だからやるな“と言っているのではなく“シミレーションをやるなら必ずセットで実際のテストをして相関を取ること“という当たり前のことを言っているだけだ。
むしろ正しい方法で日本のためにどんどん実施して欲しい。
日本のマスメディアにはせめて実際の相関が取れているのかくらいは、報道してほしいもんだ。
無理ならせめて某国営放送で検証してほしい。
筆者程度の元エンジニアでもわかるのでもっと詳しくて著名な評論家がたくさんいるだろうに。
道具や手法は、正しく使われて始めて意味があるのだ。
しつこいが超大切なので再度、述べると“仮説と検証はセット“、“シミレーションと実験はセット“、“実験と測定はセット“になり絶対にセットで必要なのである。
70年前にコメットで起きたこと(天才が国の威信をかけたプロジェクト)と全く同じことをしているように見えるのは、筆者だけなのだろうか?
歴史から学んで実行するのは、難しいのである(2回目)。
次回は残りの試験の差による結果への影響を見ていこう。
ここでオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
今回の記事で紹介したコメットの話が紹介されている名著、失敗100選などの本が安く読める。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
折角なのでさらに機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。




コメント