前回の項目でひとまず一発破壊をまとめた。

今回は、疲労破壊を説明していく。
この初心者でもわかる材料力学は疲労破壊を説明するために今までやってきたといっても過言でないくらい超重要な項目だ。
世の中のありとあらゆる製品は、この疲労破壊を考慮して耐久性が決められている。
つまり一発破壊と同様に疲労破壊の検討を行っていない製品は、存在しない。
逆に言えば製図や機械力学などにどんなに深い知識があっても疲労破壊がわからなければ機械設計は、絶対にできない。
また工業製品は、常にライバルとの競争にさらされ過酷な機能、性能を比べられる。
その機能、性能と直結する検討内容が疲労破壊だ。関係としてはトレードオフになるので悩ましい(片方を上げればもう片方は下がる)。
ギリギリまで攻めれば性能が高いが耐久性は低くなり、逆も然りだ。
つまりこの判断が製品の競争力を決めるといっても過言ではない。
では、疲労破壊の説明を始める。
破壊の一覧表だと真ん中の上から2番目、疲労破壊の全体を説明する。

材料力学的な疲労破壊の説明の前に“疲労破壊って概念的にどんな事象だ?“を次のリンクで解説しているので良かったら覗いてみてくれ。
疲労破壊ってなんだ
今まで説明してきた応力や変形はある一定の力が働いていたときの検討を説明してきた。
そのような荷重を静荷重と呼ぶ。
しかし全ての構造物は、一定の力を受け続けるということはほとんどなく受ける力は、常に変動している。
大きなものだとビルとか橋は、人が居たり居なかったり、風が吹いたり、地震がきたりと常に受ける力は、変動している。
身近な機械だとコイルスプリングなんかは、わかりやすくてスプリングが伸び縮みをする度にバネのコイルは、ねじられたり戻ったりする。

このような荷重を変動荷重、応力は変動応力と呼ばれる。一般的に横軸に時間、縦軸に力のグラフで表されることが多い。
また次にように規則的に変動する荷重を繰り返し荷重、繰り返し応力という。

では図のような引張りの静荷重と繰り返し荷重のどちらが弱い荷重で破壊するのか考えてみよう。
それはもう生活の感覚で繰り返し荷重のが早く壊れる。針金とかを何度も曲げていると折れる事象だ。
これは応力ー歪み線図の弾性域内、降伏点以下の荷重でも繰り返し掛かれば壊れる。
いくら弾性内でも荷重がかかると内部組織が変形しダメージを受けるのだ。この詳細は金属材料編で説明する。
つまり材料の降伏点以下で設計していても変動荷重が加わる場合は、いつか必ずどんなものでも破壊するのだ。
これはもはや自然の摂理だ。
物体が壊れるのは、避けられないので製品や構造物の全ては寿命(使用回数、耐用年数など)がある、というか決められて設計されている。
説明書などに記載がないのは、普通に使っていれば寿命を迎えないように設定しているからだ。
自動車みたいな変動荷重が激しい製品は、メーカーなどから厳密なメンテナンスサイクルや法律で車検を受けるなど管理されている。
気にならないのは、大抵のことはディーラーに定期的に持っていくことで寿命を迎えそうな部品は、交換されているからだ。
では疲労破壊の寿命ってどうやって検討していくのかを説明していく。
疲労限度
いきなり疲労限度と出てきたが詳しく説明していく。
疲労による破壊を管理するためには壊れる荷重、応力すなわち強度だけを見ていてもダメなので力がかかる回数も同時に考えていく。
ではどのように考えるのか説明するといある荷重を繰り返し壊れるまで材料に与えて材料内部の応力と繰り返し数をグラフにする。
また荷重も一種類だけでなく何種類も掛けて各々の壊れる繰り返し数を記録する。
また引張り圧縮だけでなくねじり、曲げ、板の回転など様々な種類の荷重を与える。

この試験を疲労試験、疲れ試験という。
めちゃくちゃ大変な試験なのだがこの結果がない材料は、設計には使えない。
ではその結果はどうなるかというと次の図のようになる。

この図をS-N線図と呼び、非常に重要なグラフになる(応力Stress-繰り返し数NumberでS-N)。
このときに$ 10^7 $回、耐えた応力を疲労限度σw、τw(ドイツ語の疲労強度Wechselfestigkeitのw)という。
さらに一発破壊と同様に引張り圧縮による疲労限度、せん断による疲労限度、曲げによる疲労限度がそれぞれ存在する。

機械設計では$ 10^7 $回以上耐えれば基本的には良いとされている。
またS-N線図の線が水平になるところを限界繰返し数と呼び、その応力を時間強度と呼ぶ。
一般的に時間強度が高い材料は高級な材料になる。
これで$ 10^7 $回耐える応力、疲労限度がわかったので設計できるかというとそう甘くないのが現実である。
実は、疲労試験での繰り返し荷重は、単純に同じ荷重の引張り、圧縮やトルク、曲げを掛けていただけで実際の構造物はもっと複雑に変動する荷重を受けている。

ではその複雑な荷重をどう考えていけば良いのか説明していく。
複雑に変動する荷重への考え方と疲労限
では複雑に変動する荷重の前に繰り返し荷重の基本の型を紹介していく。
両振り荷重、両振り疲労限
まず一番の基本は、疲労限度を求めた繰り返し応力のスタイルである変動荷重による上限の応力をσa、下限の応力を-σaとすると次のグラフになる(aは、振幅:amplitudeのa)。
横軸が時間、縦軸が応力のグラフ

そうすると平均の応力σm(平均Meanのm)は打ち消し合うので0になる。
これを両振り応力と呼びこのときの疲労の限界値はσaがS-N線図のσwになりこれを両振り疲労限度σw(要するに疲労限のこと)と呼ぶ。
片振り荷重、片振り疲労限
では次のパターンを紹介する。
ある変動荷重で発生する下限の応力を0とし上限の応力を2σaとする繰り返し応力。平均の応力はσaになる。
横軸が時間、縦軸が応力のグラフ

このような変動応力を片振り応力と呼ぶ。
この変動応力の疲労の限界の応力2σaを片振り疲労限と呼びσuで表される(なんでuなのかは、知らない)。
ここで数多くの実験より次の関係が成り立つ
・曲げによる疲労限度 片振り疲労限σu≒1.66×両振り疲労減σw
・引張り圧縮による疲労限度 片振り疲労限σu≒1.60×両振り疲労減σw
・ねじりによる疲労限度 片振り疲労限σu≒1.94×両振り疲労減
になることが知られている。
複雑な変動荷重の場合
では一見なんの法則性も見られない変動荷重の場合にどうするのか説明する。
複雑な変動荷重で発生する応力の上限をσmax、下限をσminとすると次のグラフで表される。
縦軸が応力、横軸が時間

こんな時は筆者の経験した自動車業界では、人の命に関わるので変動する上限、下限の応力の中間を平均応力σmとして次のグラフに変換される。

業界によってはもっと統計的な処理をして無駄のない平均応力σm、振幅応力σaを算出するのかもしれないが人の命に関わる製品の場合はこの方法が良いと思う。もしフーリエ級数展開を知っていればもっと細かく規則的に分けられる。
後で工業数学でフーリエ級数展開の基本を説明する。
これで不規則な変動荷重も規則性を持った変動荷重として扱える。
しかしこのような任意の平均応力σm,振幅応力σaを発生する場合にS-N線図の疲労限σwから直接、材料の寿命を求めることができない。
よって少々、細工が必要になるので紹介する。
ここまでで3タイプの変動荷重を考えてきたので一度、まとめると次の図のようになる。

疲労限度線図
では任意の平均応力σm、振幅応力σaの場合に何を使って材料の寿命を判断するのかを説明する。
基本的にはここまでで説明してきた両振り疲労限σw、片振り疲労減σuを使う。
まずは、基本の引張り圧縮の場合を考えてみる。
では横軸を平均応力σm、縦軸を振幅応力σaとしたグラフにその二つの数字(σw、σu)を使って次のような細工をする。

これを疲労限度線図と呼び、変動荷重による発生応力がこの赤線の中に収まれば$ 10^7$回持つ、つまり機械設計としては、十分に寿命があると判断して良い。
これは引張り圧縮繰返し、曲げ繰返し、ねじり繰り返しのどれにでも適用できる。
ただし材料が同じでもそれぞれの曲げ、ねじりの両振り疲労限、片振り疲労限は引張り圧縮とは異なるので間違えないようにしよう。
また引張り圧縮疲労と疲労限度線図の書き方が少し異なるのでそれぞれの書き方を次の図で紹介する。

図のように引張り圧縮、曲げ、ねじりぞれぞれの45°の青い線と交わるときの平均応力σmが曲げでは0.83σw、引張り圧縮では0.80σw、ねじりでは0.97σwであることに注意しよう。
また曲げの疲労限度線図では、振幅応力σaが0のときに平均応力σmは引張り降伏点、圧縮降伏点になることに注意しよう。
繰り返し荷重を受ける部材は必ずここまで紹介した疲労限度線図を使って寿命の計算をしよう。
ここまで検討できれば部材の強度の検討はほとんど終わりになる。
疲労破壊が発生した場合の破断面
ここまでは疲労破壊をすることに対しどのような検討をすれば寿命を考えられるかを説明してきたがここでは、疲労破壊を起こした部材の様子はどうなっているのか説明しよう。
疲労破壊はここまで説明したときに繰り返し荷重によってダメージが蓄積されると説明してきた。
実は疲労での破壊が起きた部材の破断面には次の図のような疲労の跡が残る。

その疲労によるダメージの跡は貝の貝殻が成長してできるのと非常によく似た模様になる。
それをビーチマーク(貝殻模様)と呼び非常に重要な見た目になる。
部材が疲労破壊するときは、疲労によりダメージを受け応力に対抗できる有効な断面が少しずつ減っていく。
その減った断面が入力される荷重に対し十分に小さくなると破断応力に達し一発破壊が発生する。
つまり破壊は、一発破壊のみ、疲労破壊の単体で発生することはなく組み合わせで発生する。
よって破壊の破断面には必ずそれぞれの破壊の跡が残っているので注意してよくみよう。
また疲労破壊には2種類の破壊のモードがあってそれぞれを低サイクル疲労破壊、高サイクル疲労破壊と呼ぶ。

それぞれでビーチマークの数が全く異なりビーチマークがかなり少ない場合に低サイクル疲労破壊、ビーチマークがかなり多い場合を高サイクル疲労破壊と呼ぶ。
この違いはビーチマークが数が幾つではっきりと分けられるものではないが見て誰でもわかるようなビーチマークの数が少ないのは低サイクル疲労破壊である。
この低サイクル疲労破壊が起きる条件として一発破壊ほどの大きさではないが疲労限より明らかに大きな荷重が繰り返し入力されると発生する。
まあ検討不足であることが多いが、もししっかり寿命計算してテストをしたときに低サイクル疲労破壊が発生するときは検討時には考えられなかった大きな荷重が働いているのでよく考えて対策しよう。
このように破壊は複合的に起きていて基本的な疲労破壊のメカニズムは、
になる。
この破断面をみることは超重要で筆者なんかはよくエンジンの耐久テストで壊した時にまずは掃除などは、一切せずにバラバラになった部品やカケラを全て集めてパズルのように基の形になるように集めて全ての破断面をチェックする。
その時に2次被害で一発破壊を起こしたもの低サイクル疲労破壊を起こしたもの高サイクル疲労破壊を起こしたものに分ける。
その中で高サイクル疲労破壊を起こしたものの断面をよく見て起点を探すのだ。
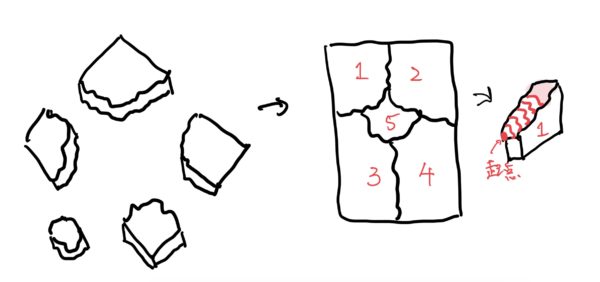
それらの解析結果からエンジン内部でどのような力が働いてどのような破壊モードで破損したのかストーリー仕立てにして正体を暴く。
このようにして破壊がどのように起きたのか犯人探しを必ず行う。
このようにしないと真の対応策が取れないのである。
また余談だが破壊した部品の破断面が2次被害で潰れて見えにくい時は、怪しい断面は少し磨くと破壊の跡が顔を出してくる。
これらの仕事を設計、テスト、材料部門などの力を総結集して解析を進めていく。
また耐久試験を行った後に明確に破損している部品がなくても亀裂(クラック)が発生していたりすることがあるのでよく見ておこう(クラックチェック)。
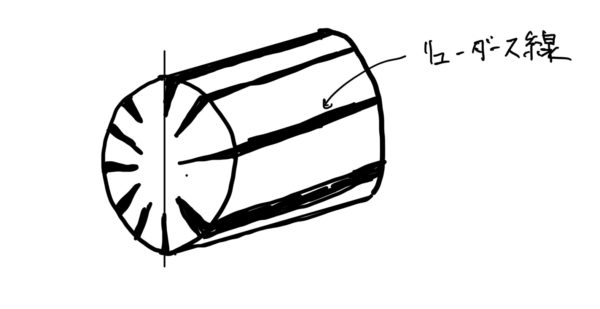
このような亀裂やリューダース線が発生していると、間もなく部品は破壊するので大抵の場合で対策が必要になる。
このように部材の寿命計算とテストは、とても大切なことなのでどんな企業でも製品開発において決して安くはない耐久試験を行い確認する。
また耐久試験の基本的な考え方は、統計的な手法によって各部品に$ 10^7 $回、負荷が掛かるように設定したりする。(色々な考え方がある。)
このように製品開発にとって寿命は、設計だけでなくテスト、品質など多くの人、部署が関わることなのでよく理解しておこう。
疲労破壊のまとめ
疲労破壊をまとめていこう。
・材料は、繰り返し荷重を受けると荷重の大きさが材料の降伏点以下でも破壊する。
・材料の疲労破壊の限界値は疲労限と呼ばれ同じ繰返し荷重が入力されたときに$ 10^7 $回以上耐える応力である。
・疲労限を表すグラフにS-N線図とものがあり、S-N線図が材料の繰り返し応力と繰り返し数の特性を表す。
・部材に入力される変動荷重には同じ荷重が同じ周期で繰り返される両振り応力、0以上の同じ荷重が繰り返し入力される片振り疲労応力がありそれぞれの疲労限度を両振り疲労限度σw、片振り疲労限度σuとする。
・S-N線図の疲労限度は、両振り疲労限度σwのことである。
・不規則な変動荷重は、変動する荷重の上限、下限をとって平均応力σm、振幅応力σaとし規則的な変動荷重に変換する。
・任意の平均応力σm、振幅応力σaの疲労限度を求めるのには、疲労限度線図が必要になる。
・疲労限度線図は材料の両振り疲労限度σw、片振り疲労限度σu、降伏点σs、一発破壊強度σbより作成できる。
・疲労破壊が発生した断面には、必ずビーチマーク(貝殻模様)が発生する。
・ビーチマークの数の多さで低サイクル疲労破壊と高サイクル疲労破壊に分けられる。
となる。
今回の解説は今までで一番、大切な内容になる。
疲労破壊の検討をされていない製品は、この世に存在しない、存在してはいけないからである。
もし今までやってないという人は、おそらく各企業で持っている計算プログラムに、この内容は必ず入っているので意識せず実施しているだけだ(知らずにやり続けると後で怖い目に会うかも)。
またこの内容は設計だけでなくテスト、品質部門などほとんどの部署が理解していなくてはならない。
製品をテストをして壊れた、市場で壊れたなど壊れたら必ず破壊の起点探し、ビーチマーク探しを行い原因を探る。
これができないと対応することができなくなるので開発を断念するか市場の製品を全て引き取るはめになる。
その時の損害は、莫大になり、時にはたった一つの部品の寿命計算を間違えただけで、そこそこ大きな企業でも経営危機や倒産までつながる場合がある(○菱自動車とか)。
最悪時は、消費者や国などの自治体に訴えられて裁判をするハメになり99%で裁判は負ける。
逆に材料屋さんも持っていない企業独自の疲労限のデータを持っていると製品開発ではとてつもなく大きなアドバンテージになる。
よって自動車会社はもちろんのこと、一見では材料に関係なさそうな企業でも材料部門を持っている会社が多い。
また何かを設計するときは材料のスペックは必ず確認して特に疲労限はよくチェックしておこう。
もし疲労限が記載されていない場合は、材料メーカーさんに聞けば必ず持っているはずだ(できればS-N線図があるとベスト)。
もしないという回答がきたらその材料屋の材料を扱うことをやめる検討をしても良いくらいだ。
そしてチェックした疲労限をもとに自分で疲労限度線図を作成しよう。材料屋さんや材料部門は基本的にS-N線図までで疲労限度線図までは作らないのでそこからは、設計が頑張ろう。
最後に急いでいてどうしても疲労限を調べる時間がない人のために筆者の経験からくるヘソクリを紹介する。
引張り強度をσbとすると
鉄鋼材料の多くは、
・両振り曲げ疲労限度σw≒0.49σb
・両振り引張り疲労限度σw≒0.73σb
・両振りねじり疲労限度σw≒0.58σb
・両振り曲げ疲労限度度σw≒0.38σb
・両振り引張り疲労限度σw≒0.33σb
・両振りねじり疲労限度σw≒0.25σb
となりここから疲労限度線図を作成することができる。
これはあくまで目安で、当然ながら鋼の種類、熱処理違い、アルミ合金の種類違い、熱処理違いで数字は変わるが多くはこのくらいになる。
これはこんなマニアアックでつまらない本ブログをここまで読んでくれた読者様へのサービスだ。
ただこの数字で絶対に大丈夫ということではないので必ず材料の疲労限度は確認しよう。
これで疲労破壊の紹介は終わりにする。少し長くなってしまったが重要な内容なので途中で区切るより良いと思って一気に行ってしまった。
基本的な破壊はこれで終わるのだが最後にたましか起きないけど、起きると最悪なクリープ破壊を次に説明する。

基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。







コメント