今回は熱応力の解説をしていく。
また熱応力だけでなく、少し関係がある残留応力も説明する。
今回は今までの応用が多く、新しく覚えたり理解するようなことは少ないと思うが、そこそこ大切なのでじっくりと取り組んで欲しい。
また初心者でもわかる材料力学を順に学びたい人はこちらの索引からどうぞ
熱応力
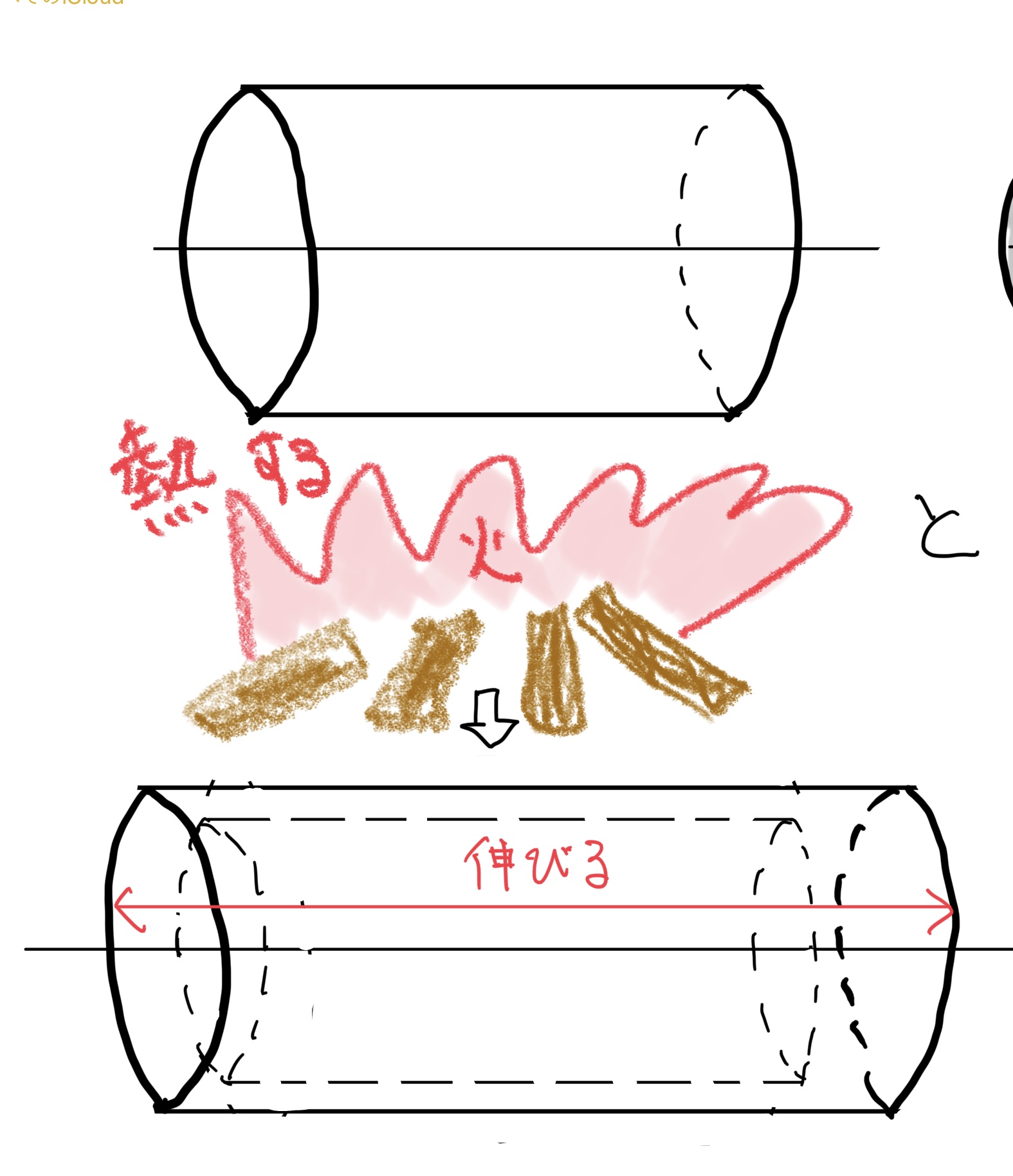
熱応力の説明の前に物体を熱すると物体は膨張することは経験上でわかると思う。
極端に言えば水は氷の状態で熱すれば液体になり、液体は熱すれば気体になりどんどん体積は増加していく。
材料力学や機械で扱う物体、材料も基本的には水と同じで熱すれば膨張する。
まずはこの膨張について考えてみよう。
次の図のような設定を考えてみる。
長さL0の丸棒の両端を壁で固定して固定部に荷重を測定するセンサー(体重計みたいなもん)を設置して丸棒の温度t0から熱を与える。
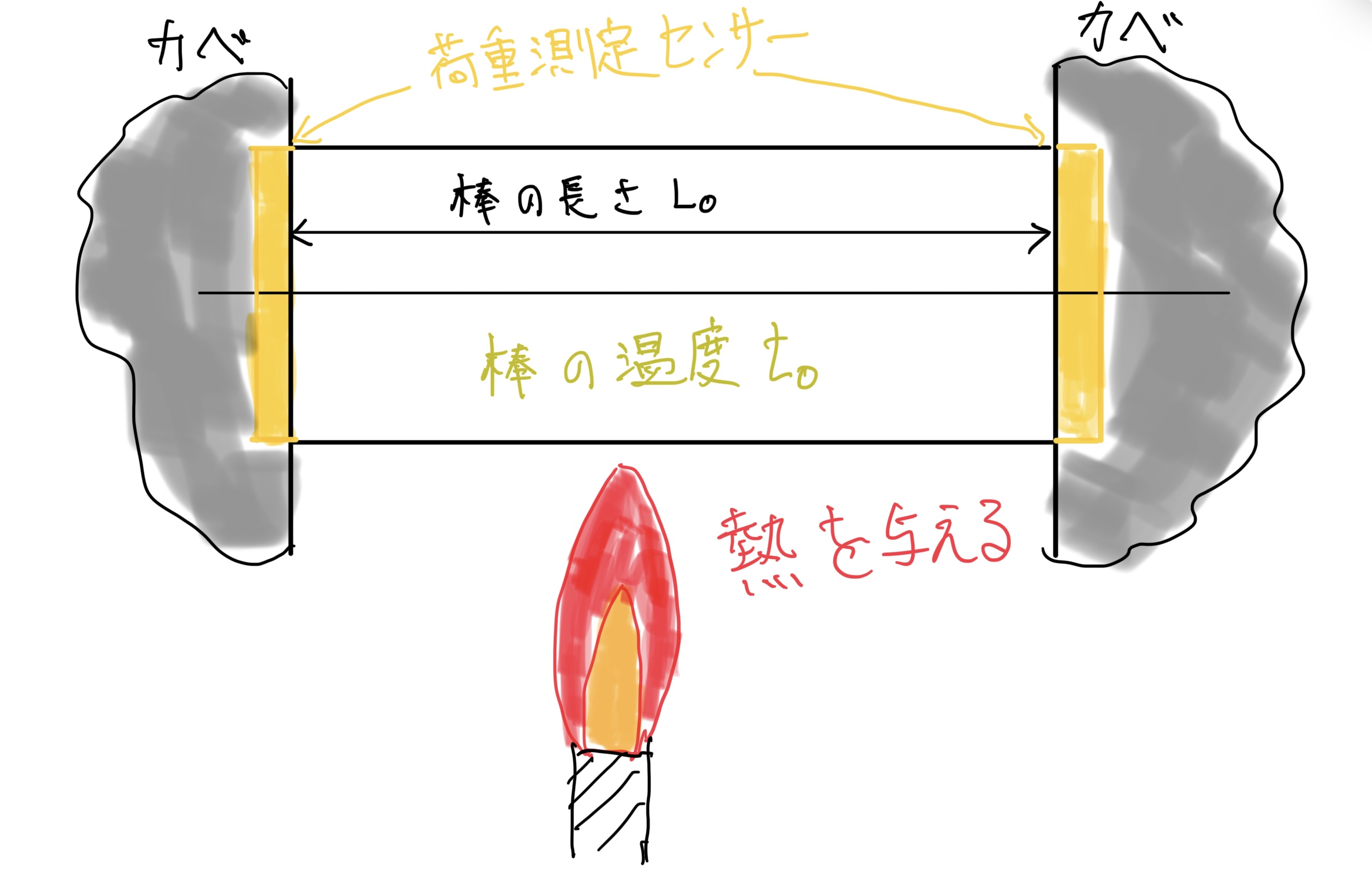
熱していくと普通に考えれば丸棒は伸びる(膨張)するのだが丸棒は壁に挟まってて物理的に伸びることが不可能だ。
だがこの伸びようとする特性が壁へ力となって働く、壁は動かないので丸棒に反力が働く、この反力によって発生する応力が熱応力だ。
文字で書くと理解が難しいので次の図を見て欲しい。
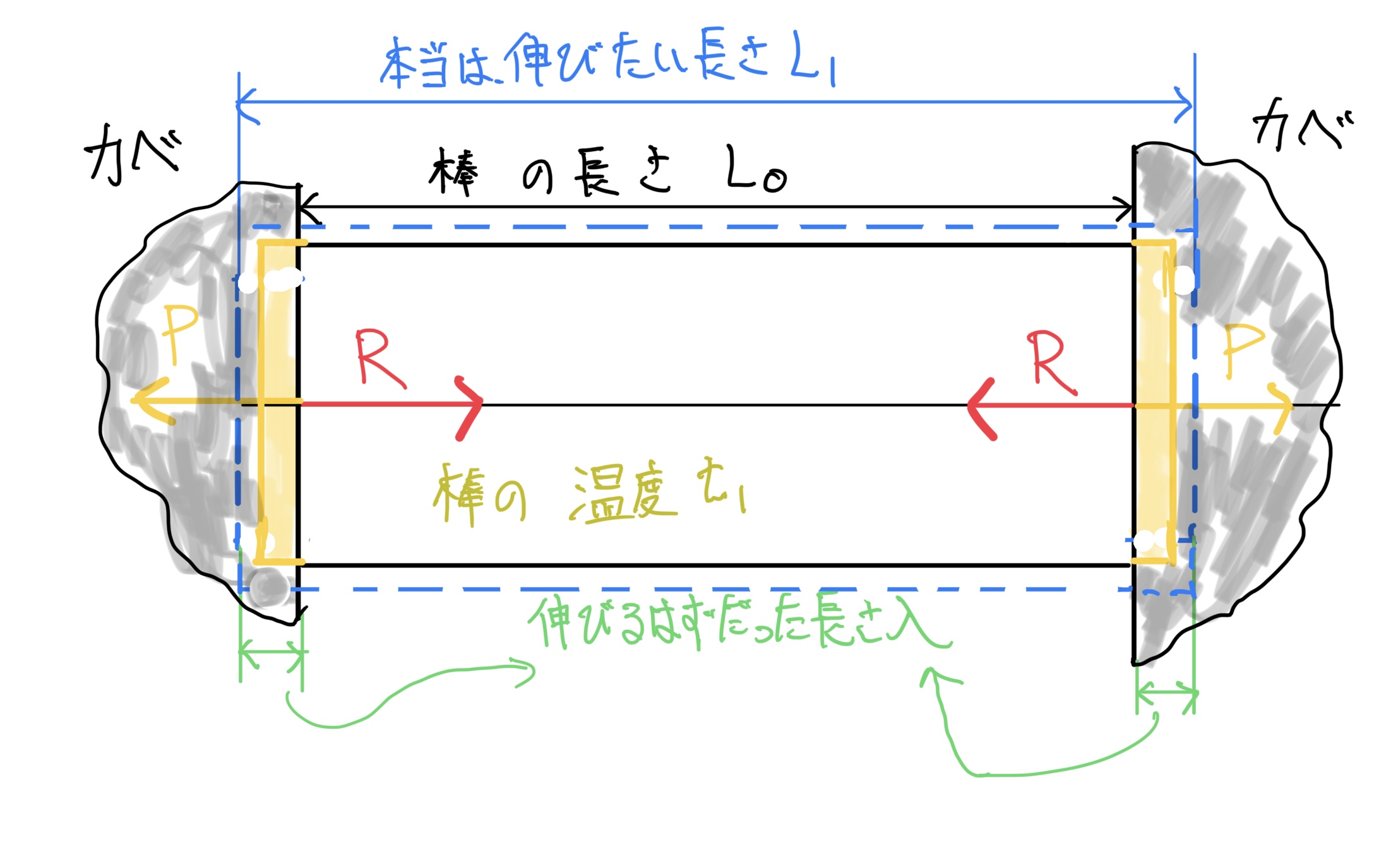
ここで一旦、状況を整理しよう。
・元の丸棒の長さ L0
・本当は伸るはずだった丸棒の長さ L1
・丸棒の温度は最初は、t0で熱した後は t1
・壁に設置された荷重測定器の荷重は P
・丸棒に掛かる反力は R = P
・丸棒の伸びるはずだった伸び量 λ = L1-L0
とする。
実はこの中で実際にわかる数字は元の長さL0と温度差がt1-t0と測定器の荷重Pからわかる反力Rの3つである。
よってこの3つを使って反力Rを求めていく。
ここで新しい概念である線膨張係数α(アルファ)という数字を使う。
これは簡単で物体の温度が上昇するとどのくらいの割合で伸びる(膨張)するかを示すのが線膨張係数αだ。割合を示すので歪みのように単位はない。
早速、式を立てて行こう。線膨張係数αを使えば丸棒の伸び量λが次のように表される。
$ 丸棒の伸び量λ=L1-L0=α(線膨張係数) ×L0(元の棒の長さ)×(t1-t0)(丸棒の温度差) $
次に伸びるはずだった量λはカベのせいで伸びることができないので丸棒が圧縮されていることになる。
これは初心者でもわかる材料力学1を思い出して欲しい。
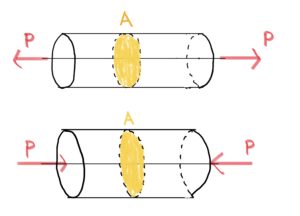
いったんカベのことを忘れてもらって上で丸棒に外力Rが与えられた場合の縮む量をλと考えればわかると思う。
ここで弾性の関係から歪みと弾性係数が分かれば熱応力が分かり、丸棒の面積がわかれば熱応力から測定された荷重P=Rがわかる。
では、順に見ていこう。まず丸棒の歪みεを求める。注意としてここで圧縮歪みと考えるので歪みの計算の分母は伸びた長さL1になる
$ 丸棒の歪みε=\frac{L0-L1}{L1}=\frac{-λ(丸棒の伸び量)}{L0+λ(丸棒の伸び量)} =\frac{-1}{1+\frac{λ}{L0}}×\frac{λ}{L0} $
ここでちょっとずるいのだが$ \frac{λ}{L0} $で元の長さL0に対して伸び量λはとっても小さいので$ \frac{λ}{L0} $は、0とみなす。
このような解釈や省略はエンジニアリングでは頻繁に発生するのだ。
なぜならば学問のような厳密解を求めるのとは違って現実に使える解が欲しい場合が多いからである。このあたりの加減は後に数値計算講座(仮)で解説する。
さて戻って式を見て行こう。結局、丸棒の歪みεは次の式になる。
$ 丸棒の歪みε=-\frac{λ(丸棒の伸び量}{L0(丸棒の元の長さ)} $
で丸棒の熱応力σは丸棒の弾性係数をEとして線膨張係数αを使うと次の式になる。
$ 丸棒の応力σ=E(弾性係数)×ε(丸棒の歪み)=E×-\frac{λ}{L0} $
$ =-E×α(線膨張係数)(t1-t0)(丸棒の温度差) $
となる。
マイナスなので圧縮であることがわかる。
ここで丸棒の断面積をAとすると測定器で測定した外力Pから丸棒の反力Rは等しく圧縮力なので次の式で表される。
$ 反力R=-σ×A(断面積)=AEα(t1-t0) $
で表される。
当然ながらこれまで熱した場合を述べてきたが冷却すると符合が逆になり引張り応力が発生する。
ただし筆者の経験上では機械材料の多くが冷却した場合の縮み量は熱したときの線膨張係数に比較しかなり小さいのであまり気にしたことがない。
最も筆者が内燃機関、エンジンの設計者だったからかもしれない。
ただエンジンも摂取−15℃から40℃の環境でも保証するように設計していても冷却による縮みは気にしたことがない。
ただしここで出てきた線膨張係数αはものすごく大切な概念なのである。
線膨張係数αは材料特有の物性値で熱応力を求める以外にも高温度化で使用される機械では必ず材料がどのくらい膨張して寸法が変化するのか必ず検討しよう。
ちなみに線膨張係数αは基本的には物性値に記載されているがもしわからなければ材料の取引先等に聞いてみよう。
まともな会社なら必ずデータを持っているはずである。
残留応力
いきなり残留応力なんて難しい言葉が出てきて驚いたかな?
これは概念自体は、簡単だけれどもとても大切な特性なので是非、理解して欲しい。
ここまで熱応力を解説してきた熱を与えれば物体は膨張するし場合によっては応力が発生していることが理解できたと思う。
また物体を放っといて元の温度に戻れば物体は元の大きさに戻り応力も無くなるはずである。
しかーし、実際には元の温度に戻っても一部の応力は発生し続けるのである。これを残留応力と呼ぶ。
代表的な残留応力が熱応力で説明したような圧縮残留応力である。
説明してきた熱応力での残留応力を図で表すと次のようになる。
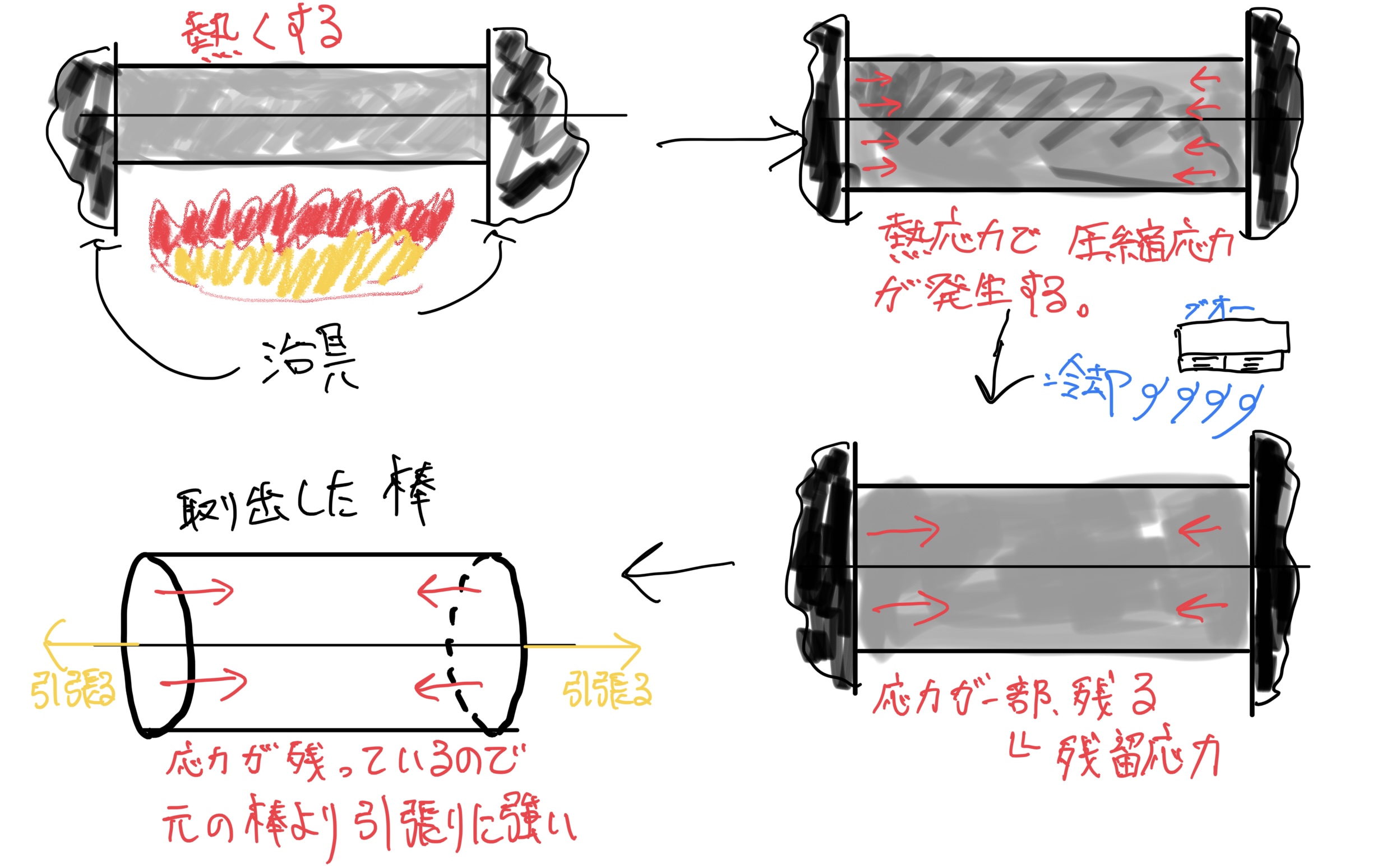
上の図の場合には圧縮残留応力が残って引張りに対し元の材料の強度に残留応力分が足される。
残留応力は熱だけでなく物体を叩いたりしても発生する。図が例だ。
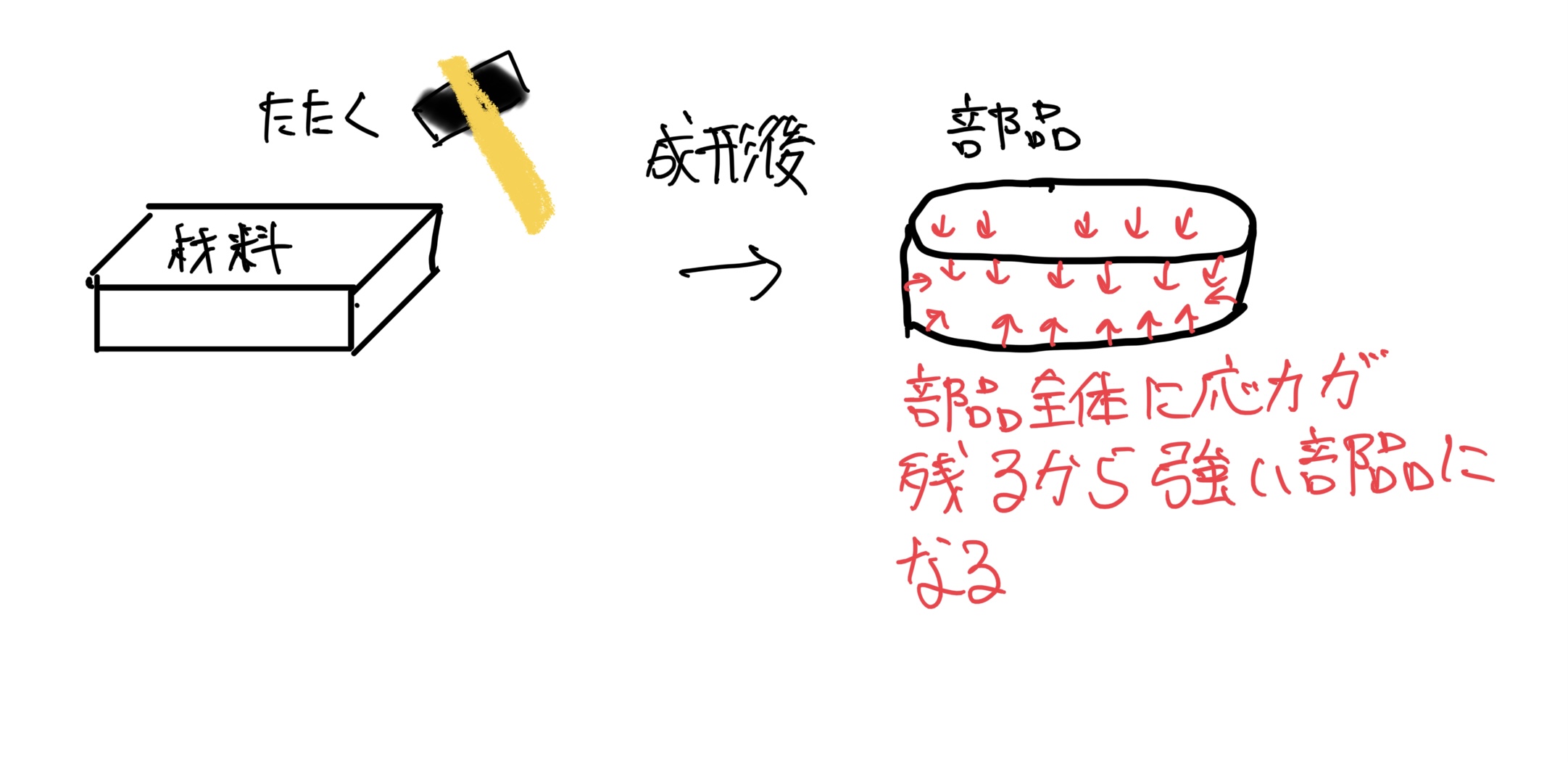
まあ一般的に鍛造と言われてる製法で造られた部品の強度が高い理由の一つでもある。
このように熱で処理する場合は焼き入れ、焼きなまし(残留応力だけではないけど)や加工硬化と製造工程で残留応力が発生することは頻繁に存在するので頭の中に入れておこう。
面白い処理だとショットピーニング(WPC処理 株式会社不二機販、株式会社不二製作所、株式会社不二WPCの登録商標でほとんど業界スタンダード)は大雑把に説明すると成形した部品に細かい鉄球を何千粒と当てて表面に圧縮残留応力を発生させて強度を上げる処理だ。
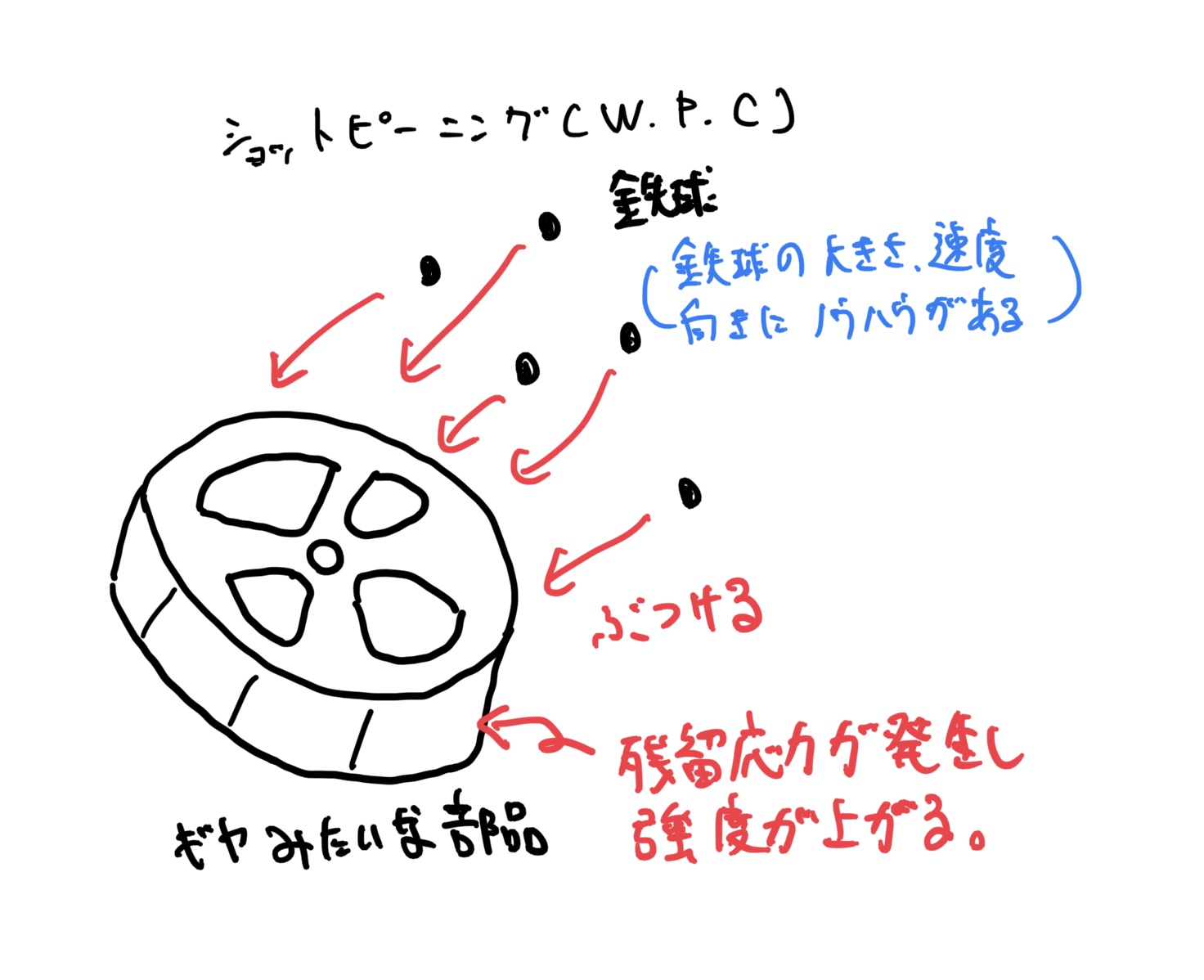
筆者の経験だと条件にもよるが疲労強度で2割くらい上がったこともある。
まあこの辺の熱処理、表面処理、金属材料、製法はのちに機械設計講座でぞれぞれ詳しく説明する。
ちなみに筆者は残留応力の理論式みたいなのを見たことがあるがよく分からなかった。一部、業務で利用したことがあるので後にテクニックとして紹介する。(マイナー則とか)
まとめ
今回のまとめ
・機械設計、材料力学で扱う物体は温度変化によって膨張、収縮する。
・物体が熱を与えられて膨張する割合を線膨張係数αで定義し物体固有の値である。
・熱などで物体に発生した応力の一部は残り続けその応力を残留応力と呼ぶ。
・機械設計するときは機械の環境温度変化を考えて線膨張による寸法変化を把握しよう。
になる。
ちょっと長くなってしまった。
次回は、機械設計でよく使う円環応力とトラスの解析を説明したい。
それが終わればやっと梁(はり)の応力が説明できてひとまず材料力学は区切れる。
基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。





コメント