今回までで一発破壊の引張り、せん断力による破壊を説明してきた。
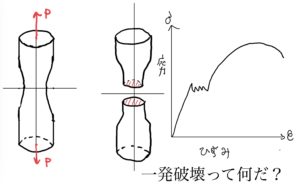

今回は、一発破壊のラストの曲げによる破壊を説明していく。
一発破壊の表で見ると一番下の部分になる。
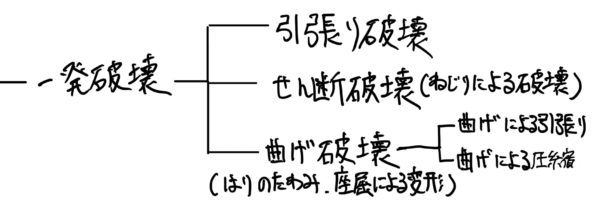
では早速、説明して行こう。
曲げによる応力のおさらい
ここで曲げによって発生する応力のおさらいを軽くしていく。
まず曲げによる変形の代表ははりのたわみと長柱の座屈になる。
では、部材に曲げモーメントを加えるとどうなるかおさらいしていこう。
断面が四角で高さh,幅bの角材の両端に曲げモーメントMを加える。そうすると図の下方向に部材はたわむ。

その時に部材の断面ではどのような応力が発生しているか考える。
例えば図の部材の真ん中でカットして考えると部材の下側は引っ張られて、上側は逆に圧縮される。
つまり下端には引張り応力、上端には圧縮応力が発生する。

図では先走ってしまったがその応力は、断面係数Zによって求められる。
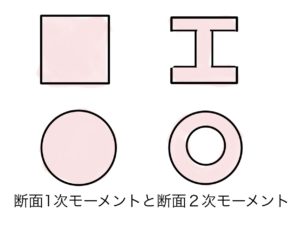
断面係数Zは$ Z=\frac{I}{h} $(断面2次モーメントI,中立面からの断面高さh)で求められ引張り応力をσp、圧縮応力σcとすると
$ σp=\frac{M}{Z} $
$ σc=-\frac{M}{Z} $
となる。
この変形は断面の中心に行くほど歪みが小さくなるので各応力も小さくなり真ん中では0になる。(中立面)
またこれらの応力は曲げモーメント(力ではない)に逆らって発生するので応力を全部足し合わせると0になる。
ただし各応力のモーメントを足し合わせると部材に掛かっている曲げモーメントと釣り合う。
こんなところが基本的な曲げモーメントによる応力の特性になる。
曲げモーメントによる破壊
では曲げモーメントによる破壊を考えていく。
曲げモーメントMBを加えた時に部材が壊れたとすると先程のおさらいから部材に働く最大引張り応力が断面係数Zでわかるので破壊応力がわかるはずである。
$ σB=\frac{MB}{Z} $
と簡単に求まる。
この式より逆に部材の引張り強度σsから破壊する曲げモーメントが算出できると思われる方が多いと思うがそうならないのである。
ねじりと一緒で最大引張り応力が引張り強度、降伏点に達しても部材の内部の応力はそれら以下のため破壊したり、降伏しないのである。
では、曲げの破壊の様子を見るために応力ー歪み線図、応力ーねじれ角線図のように曲げーたわみ線図というものがあるので見ていこう。
粘りのある材料に破壊するまで曲げモーメントを掛けていくと次のグラフのようになる。

ねじりの時と一緒で部材の引張りの降伏点から求めた曲げモーメントより大きな曲げモーメントMsでモーメント量は増加せずたわみのみが増加していく。
そう、この曲げモーメントMsが一定の間に部材内部で転位が進んでいるのだ。
部材内部、全体の転位が終わると曲げモーメントは、再びたわみに応じて増大していき塑性変形から破壊に進む。
このときの内部の応力を詳細に見て行こう。
ねじりのときと同じように曲げモーメントMsによる転位が発生している間の部材内部に発生する応力は一定であると仮定する。
ある長さの部材で断面は四角で幅b,高さhに曲げモーメントMsが掛かっていて転位が進んでいる状態を考える。

ここで応力をσsとするとおさらいより断面内部に発生する応力のモーメントの総和は、曲げモーメントMsに等しいので次の式が成り立つ。
モーメントMs=微小区間dzの力(σs×bdz(微小区間の面積))×距離zの中立面から端までの積分
$ Ms=2\int_{0}^{\frac{h}{2}}(σsbdz)z=2bσs\int_{0}^{\frac{h}{2}}zdz=\frac{bh^3}{4}σs $
$ σs=\frac{4}{bh^2}Ms $
になる。
またここでねじりと同じように降伏直前での部材の端の応力をσ0とすると曲げモーメントMsから断面係数Zを使って次の式が成り立つ。
$ Z=\frac{I}{\frac{h}{2}}=\frac{bh^2}{6}$
$ I=\frac{bh^3}{12} $
$ σ0=\frac{Ms}{Z}=\frac{6Ms}{bh^2} $
より先程のσsと比較すると
$ σ0=\frac{3}{2}σs $
となり表面応力が部材の降伏点の1.5倍になるまで降伏しないことになる。
ただしこれは、超粘りのある材料の時だけで実際にはもうちょっと低かったりする。
実際に曲げモーメントーたわみ試験を実施するとグラフは次のようになる。

このように明確な降伏点がなく、だらだら変形するので判断が難しい。
だから実際には部材によって降伏点をσsとし発生応力をσ0と置くとσs<σ0<1.5σsくらいで使う。
気の利いた材料屋さんだとスペック表に曲げ強さが載ってるので確認できる。もしデータがないなら聞けばデータを出してくるはずである。
最悪、なければ曲げーたわみ試験をやるしかない(大体の材料は曲げ強さのデータがある)。
その時は次の図のような感じでテストする。

たわみ量は、部材の計測点に歪みゲージを貼っておけばわかるし、荷重は両端の台座にロードセルを付けとけば把握できる。
そんなに難しくなく時間もかからないのでデータがなければやっても損はないと思う。
もし要望があれば詳細なテスト方法を説明する。
曲げ応力による一発破壊のまとめ
では曲げ応力による一発破壊をまとめる。
・曲げモーメントによる一発破壊は、モーメントによって発生する部材内部の引張り応力で破壊する。
・曲げモーメントによる一発破壊では材料の引張り降伏点と部材の曲げ降伏点は、一致しない。
・曲げモーメントによる変形で部材内部で転位が発生しているときは部材内部の応力は一定。
・理想的な粘りのある材料なら部材の降伏点の1.5倍の応力まで降伏しない。
・実用材料では、曲げーたわみ試験より明確な降伏点が見られないので材料の降伏点の1.5倍未満で考える。
・材料の曲げ強さはスペックに基本的には記載されている。
・材料の曲げ強さがわからない場合は、曲げーたわみ試験をやってみよう。
となる。
まあ曲げといっても考えていけば結局のところ引っ張り応力による破壊になる。
若干、特殊な発生の仕方をするだけでただの引張り応力なので難しく考えないようにしよう。
実際にこの曲げ強さだけを使って構造物の検討をすることはほとんどない。
ただしこれから説明する疲労破壊に使う重要な値の一つになるので理解しておこう。
一発破壊のまとめ
ここまでで基本的な一発破壊は全て説明した。
種類としては次の表になる。

個々のおさらいはそれぞれの項目を見てもらうことにして全体をまとめると
・材料は基本的にどんな応力に対しても降伏点以下で扱うこと
・降伏点が明確に見られない材料の場合は、0.2%耐力以下で扱うこと
・いずれの応力にせよ応力ー歪み線図、トルクー角度線図、モーメントーたわみ線図は重要なので読めるようにしよう。
・テストが終わった部品は必ず観察して一発破壊や降伏してないか必ず確認しよう。
・テストで部品が破損したら破断面をよく観察してどんな応力で破損したのか確認しよう。
になる。
普通の設計をしていれば基本的に一発破壊をすることは、まずない(材料の引張り降伏点以下で設計する)。
では、どのような場合に一発破壊するのかというとどこかが疲労や腐食で破損して想定以上の荷重が部品にかかった場合や意図しない衝撃荷重を受けたときに一発破壊を起こす。
どちらかというと副次的に発生する形態なのだ。
しかしながら一発破壊だけではないが破壊の原因を掴めないと対応、対策が取れず何も進まなくなる。
もし破壊の現場(自分の担当製品以外も気にすると良い)に出くわしたら積極的に見に行って破壊の原因を特定するスキルを身につけよう。
次回から超大切な疲労破壊を説明する。

基本的に本内容の教科書は存在せず筆者オリジナルだが筆者が学生から使っている教科書を紹介する。
もう一点、機械設計で必須の本があるので紹介しよう。
はっきり言って中身は不親切極まりないのだがちょっと忘れた時に辞書みたいに使える。このブログを見てくれれば内容が理解できるようになって使いこなせるはずだ。
またよく使う規格が載っているので重宝する。JISで定められて機械材料の特性が載っている。
多くの人が持っていると思うが持っていない人はちょっとお高いが是非、手に入れて欲しい。但し新品は高いので中古で購入を考えている方は表面荒さの項目が新JIS対応になっているのを確認することを強くオススメする。
さらにオススメしたいのがアマゾン キンドル アンリミテッドだ。アンリミテッドだと数多の本が月会費だけで読める(漫画〜専門書まで幅が広い)。
しかも流石、本屋が原点であるAmazonだけあって機械工学の専門書がそこそこ揃っていてかなり使えるサービスだ。
特に機械工学の専門書は高額になることが多いので少しだけ読みたい分野の本を眺めるのに非常に役に立つので是非、オススメしたい。
また本ブログをキッカケとしてエンジニアとしてステップアップして大きな仕事を掴む手段の一つとして転職するのも一つの手だ。
やはり予算の大きい機械設計、規模が大きい機械設計、大きな仕事をする場合は日本においては大手に入って仕事をする方がチャンスの機会が多いと思う。
私も最終的に転職はしていないが自分の将来を模索していた時期に転職活動をしていくつか内定を頂いたことがある。
折角なのでその経験(機械設計者の転職活動)を共有できるように記事に起こしたので参考にして頂ければ幸いだ。







コメント