前回までのページで一通りはりに関する材料力学を説明してきた。
今回ははりのたわみを求めるのに必要な代表的な断面二次モーメントを紹介する。
さらにただ式を羅列するばかりでは意味がないので筆者が実際に出会った例をつけながら説明していこう。
もし設計中に早見表的に使えると思うので良かったら使って欲しい。
ただし断面二次モーメントを自力のみで求める能力は必須ではないが意味は理解しないとかなりまずい。
忘れてしまった、もしくは始めて見る人はこちらを参照して意味を理解して欲しい。
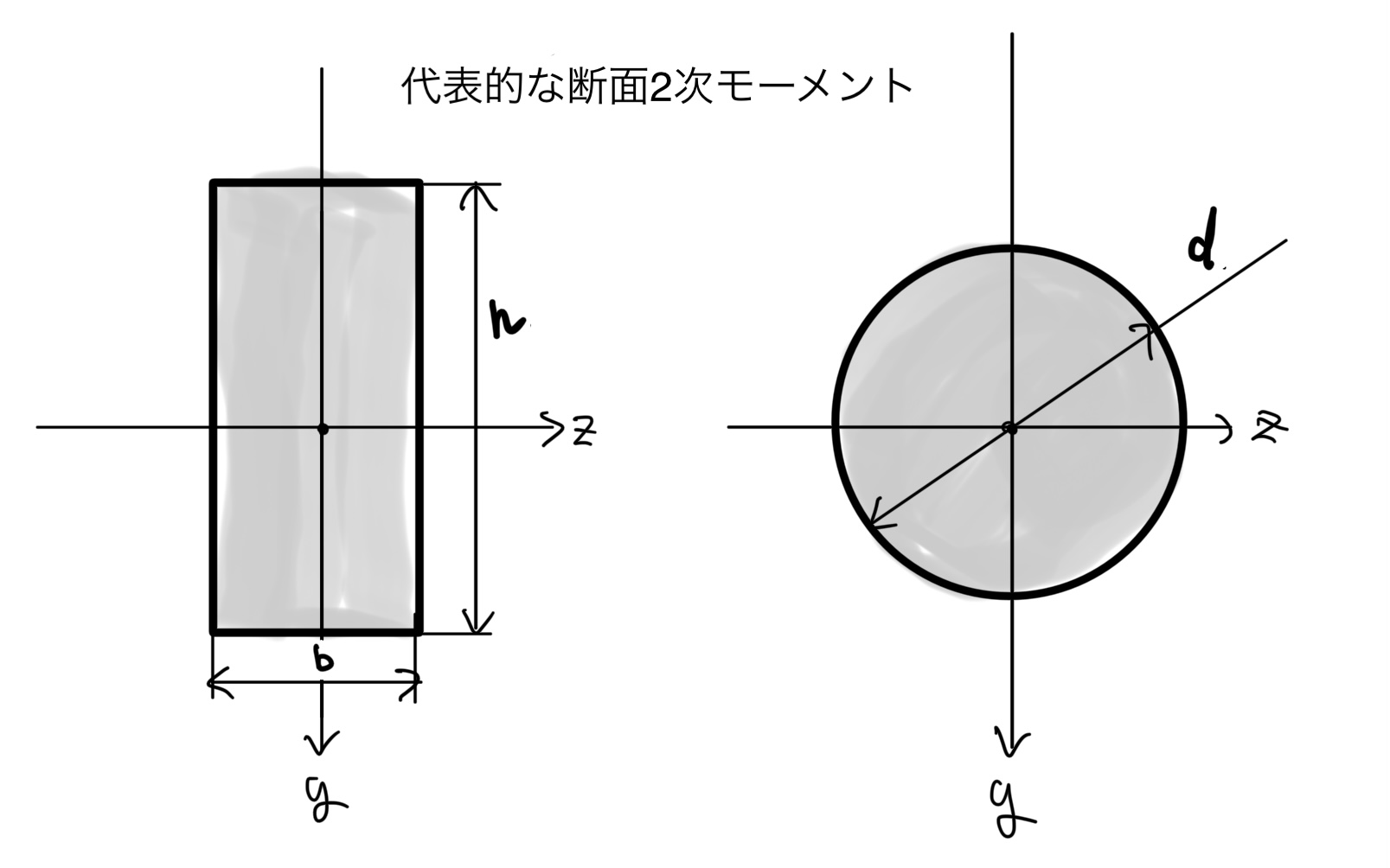
代表的な断面の断面二次モーメント
ここからは代表的な断面の断面2次モーメントを紹介していく。これから紹介する断面を組み合わせれば実際に使用されている断面の99%はカバーできるはずだ。
四角断面
幅bで高さがhの四角断面の断面二次モーメントI
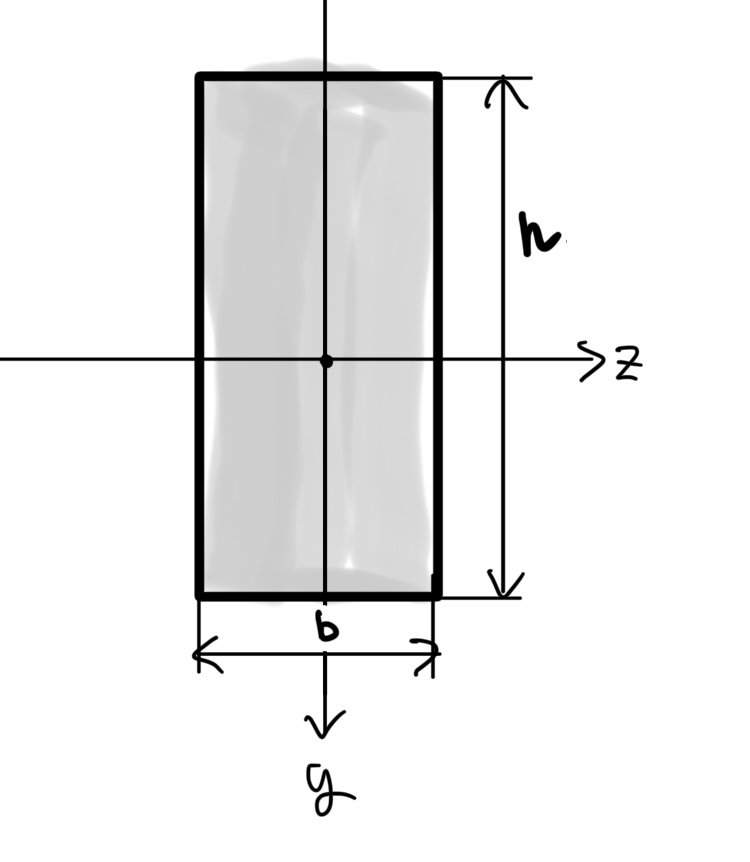
$ 面積A=bh $
$断面2次モーメントI=\frac{bh^3}{12} $
これは基本形で全てがここから始まる。
三角形断面
高さがh、底辺がbの三角形断面の断面2次モーメント
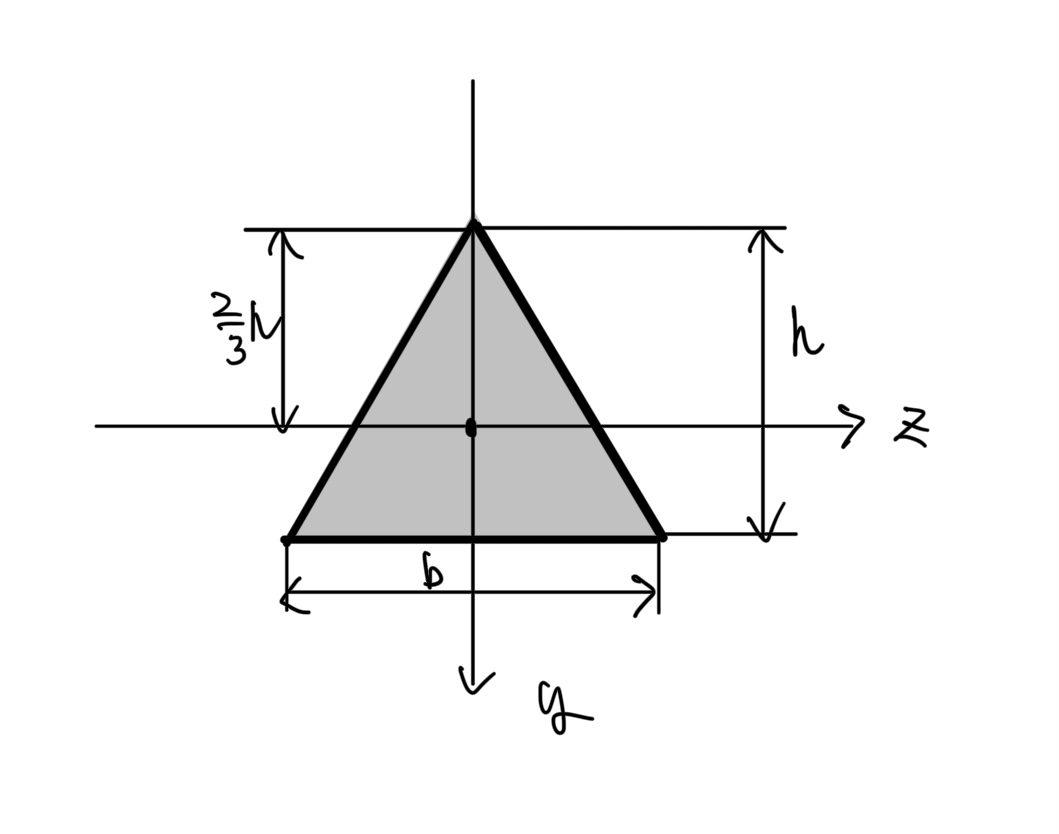
$ 面積A=\frac{bh}{2} $
$断面2次モーメントI=\frac{b}{h^3}36 $
三角形断面だけでは使わないが他の形状との組み合わせで使う。
円形断面(軸の断面)
直径がdの円形の断面の断面二次モーメントI
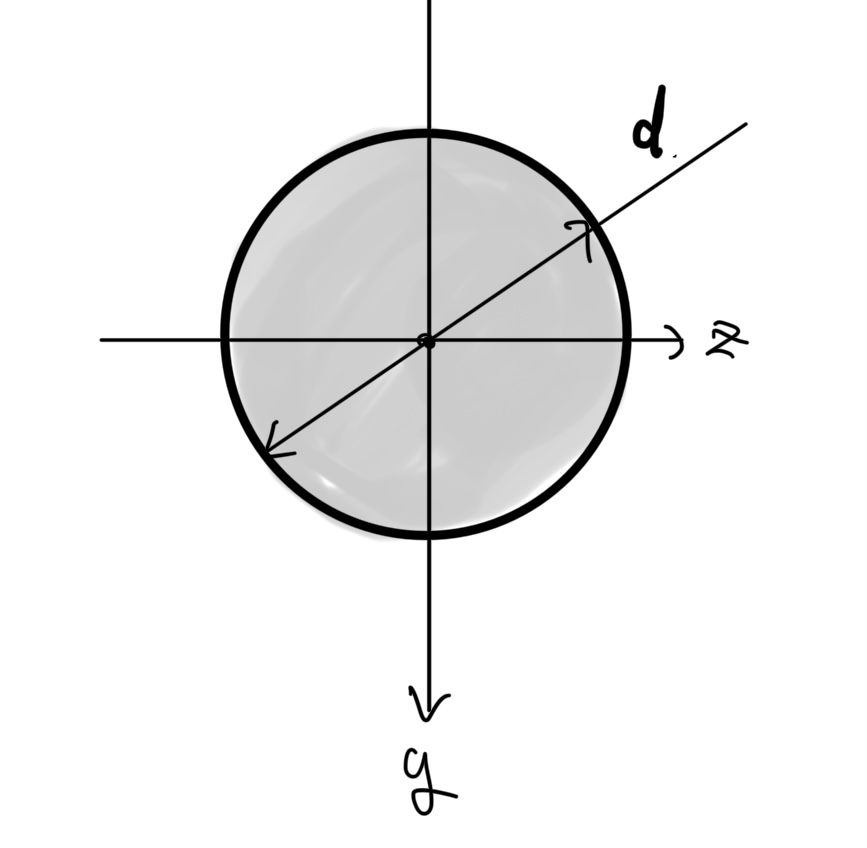
$ 面積A=πd^2 $
$ 断面2次モーメントI=\frac{πd^4}{64} $
使用例の代表は荷重が掛かる軸だ。
筆者の専門のエンジンで言えばピストンピン、クランクピンなど多数だ。
中抜き円形断面(中空軸の断面)
外径がd1で内径(中抜き径)d2の中抜き円形断面の断面二次モーメントI
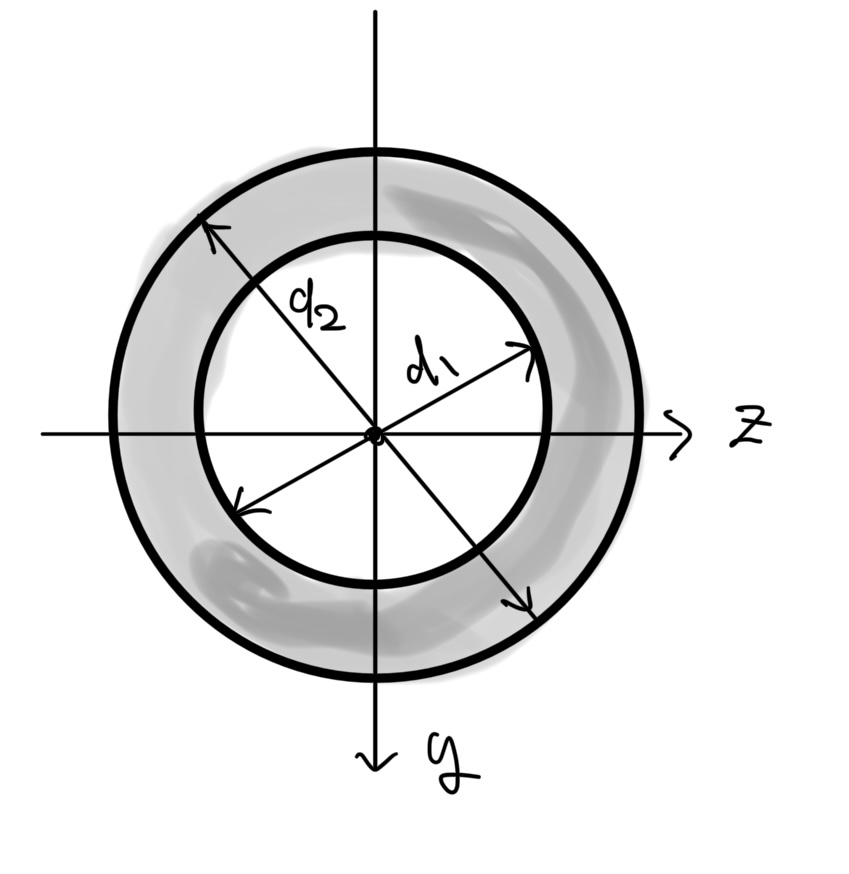
$ 面積A=π(d2^2-πd1^2) $
$ 断面2次モーメントI=\frac{π(d2^4-d1^4)}{64} $
これの使用例は少しでも軽くしたい機械の軸はほとんど中空軸である。むしろただの丸棒の軸を見たことはほとんどない。
菱形断面(アルミ冊子などの角材)
辺の長さaで全て等しい菱形の断面の断面二次モーメントI
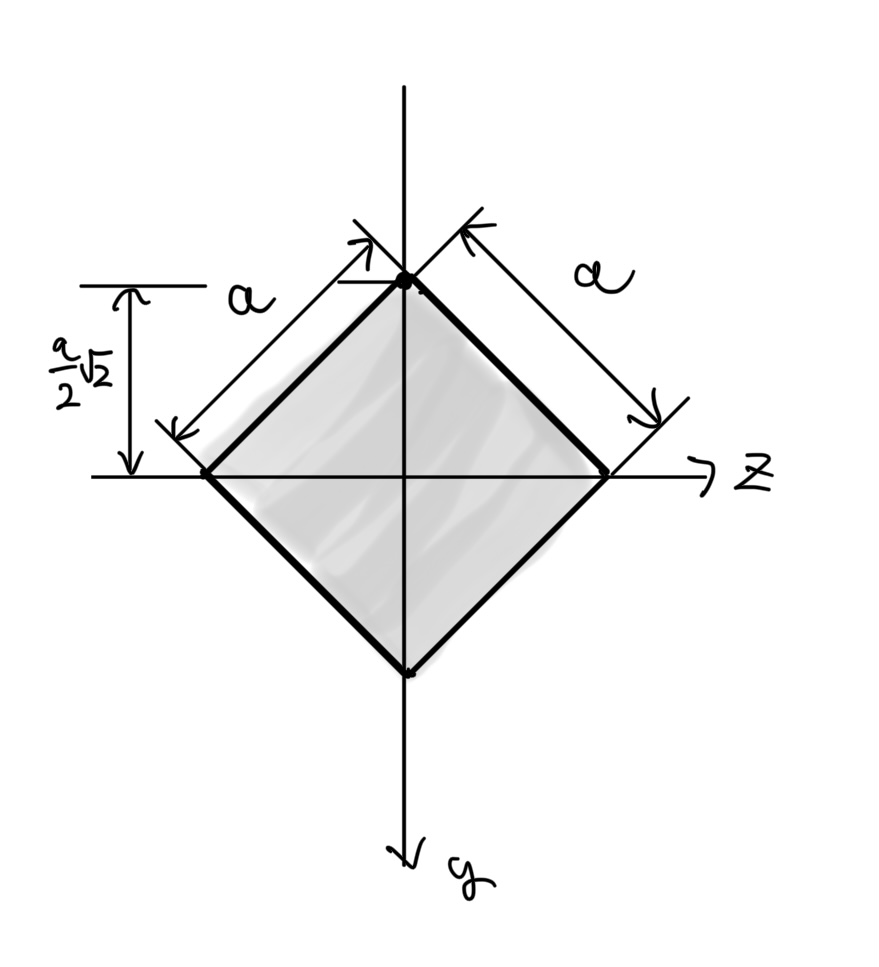
$ 面積A=a^2 $
$ 断面2次モーメントI=\frac{a^4}{12} $
これはホームセンターとかで普通に売っている角材だ。機械設計だとリブの先端の形状を菱形にして断面二次モーメントを稼ぐ。
後で説明するが鋳造で部品を作る場合に非常に成型性がよく金型も長持ちする形状になる。
I型断面(建築系に多いのかも)
分厚い幅をb、薄い幅をt、全高さがhで分厚い部分の高さがcのI型断面の断面二次モーメントI
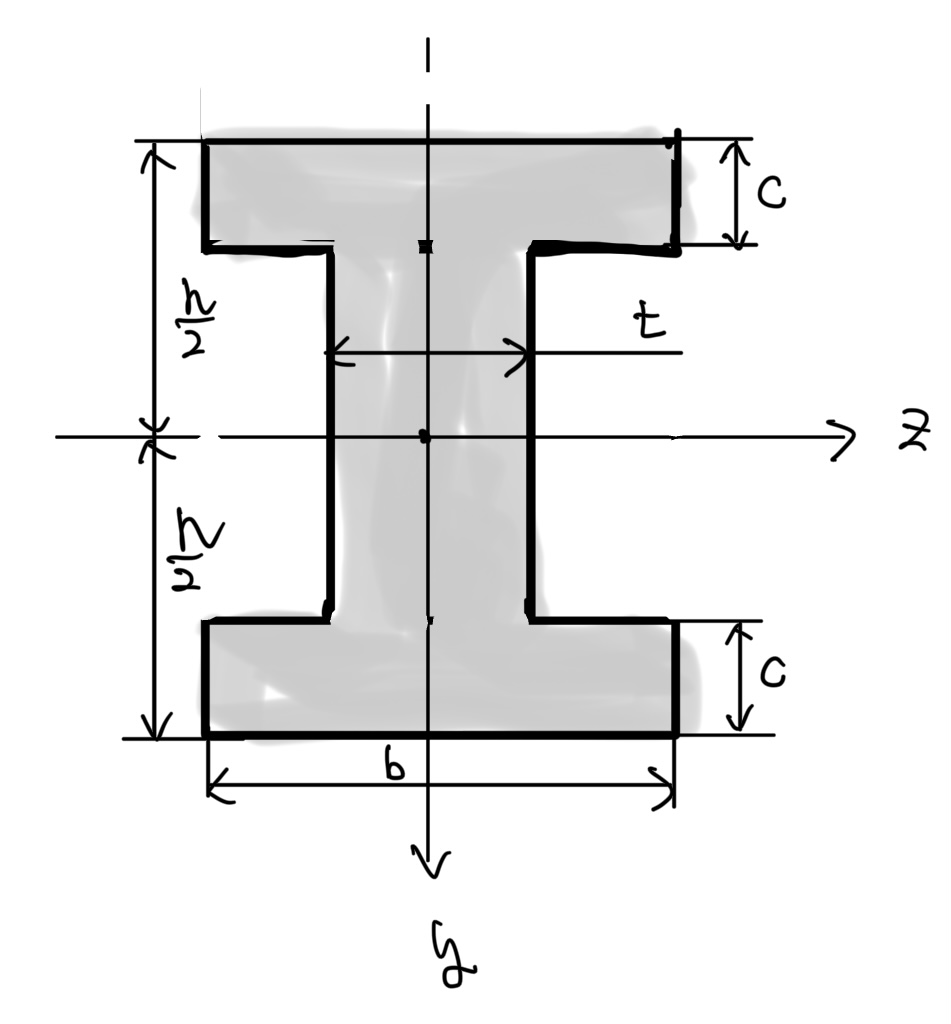
$ 面積A=hb-(b-t)(h-2c) $
$断面2次モーメント I=\frac{bh^3}{12} -\frac{(b-t)(h-2c)^2}{12} $
これもホームセンターでよく売っている角材の一つだ。実際の機械設計では自動車のフレームなどに使う。筆者の専門のエンジンではコンロッドの断面形状として採用することがある。一般的に剛性メンバーとしてよく使う断面だ。
両切り欠き円形断面(継ぎ手やキー)
文章で表現するのが難しいのだが半径がdの円で切り欠き角度がαの断面の断面二次モーメントI(図を見てくれ)
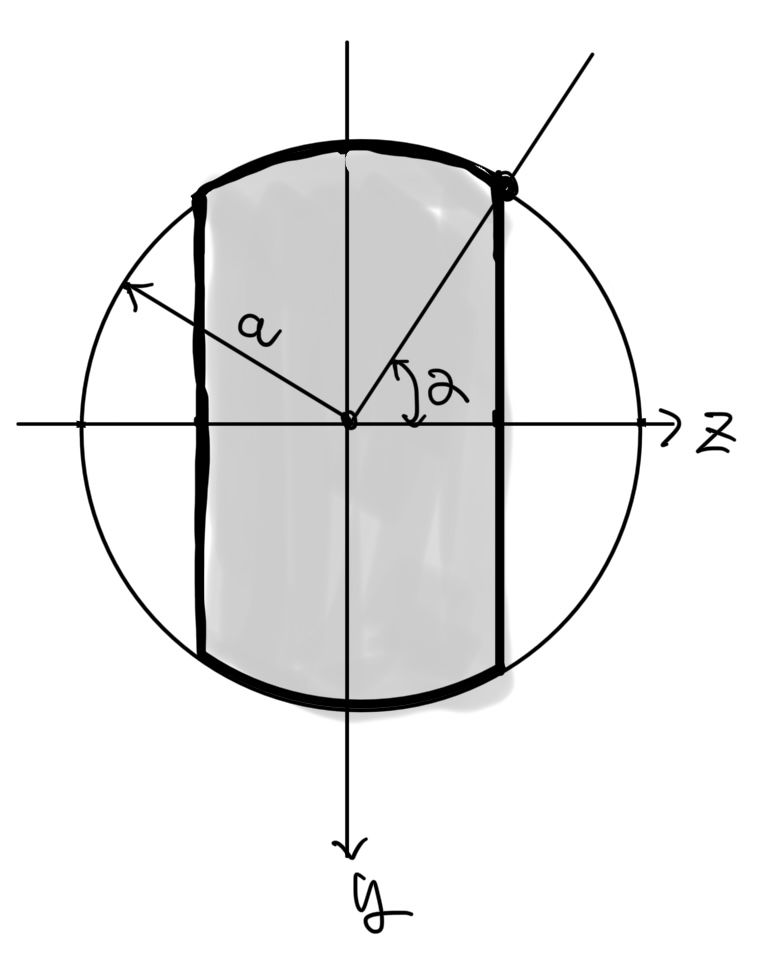
$ 面積A=a^2π-a^2(α-sinα) $
$断面2次モーメント I=\frac{a^4}{24}(6π-12α+8sin 2α-sin 4α) $
これはかなり重要な断面だ。
使い所は軸と軸を繋ぐときに継ぎ手として使う(オルダム継ぎ手)。こ回転力を伝える重要な機構の基本だ。
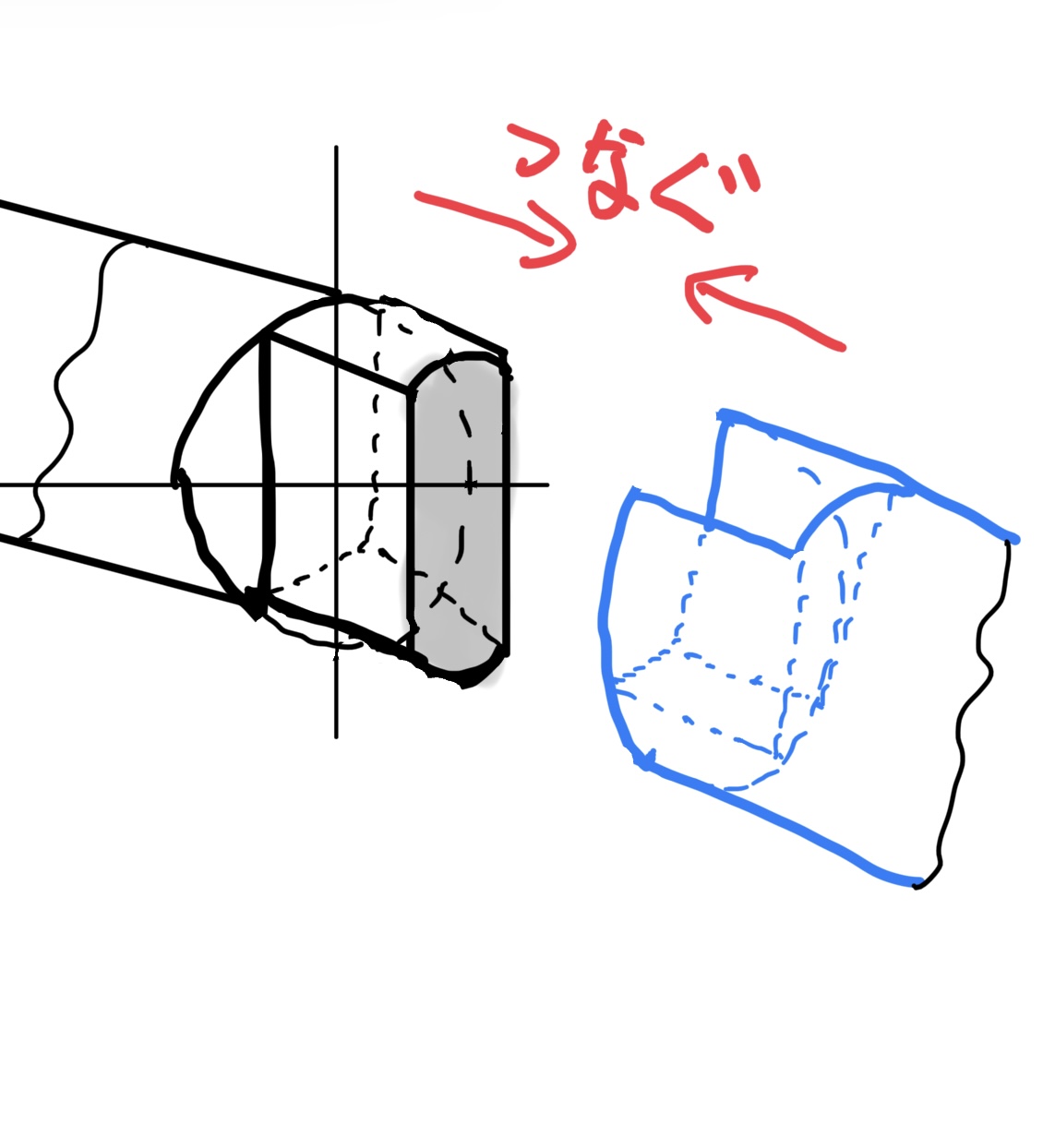
継ぎ手以外にも軸の回り止め(キー)など様々な機械要素で使う重要な断面だ。
重要な機械要素については別途、専門のページで紹介する。
正六角形断面(ハニカム構造)
辺の長さがaの正六角形断面の断面二次モーメントI
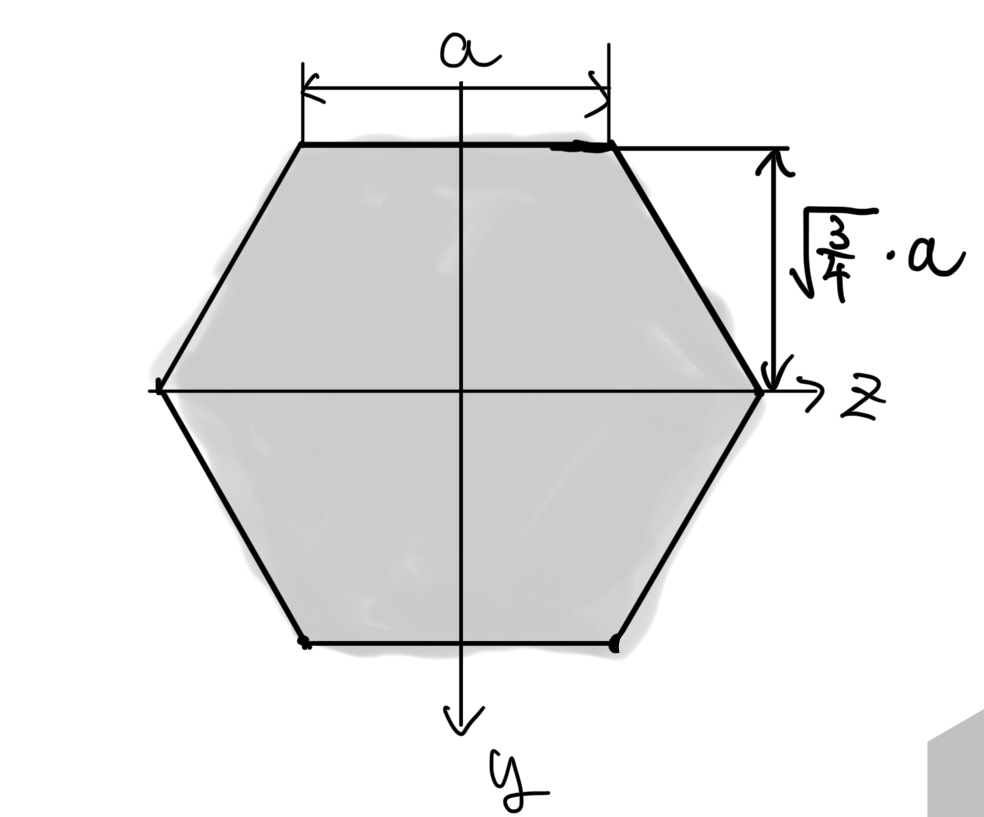
$ 面積A=\frac{3\sqrt{3}}{2}t^2 $
$ 断面2次モーメントI=\frac{5\sqrt{3}}{16}a^4 $
これが有名なハニカム構造の断面である。筆者は厚みが大きく取れるリブの断面形状でよく利用する。
鋳造で作る部品で幅が小さいリブだとこの形状が正確に成型できないことがあるのでよく考えて使わないとただの四角断面の隅にRをつけただけの形になって意味がなくなるので注意が必要だ。
まとめ
よほど特殊な断面以外の断面二次モーメントはこれで求まると思う。
一見すると複雑な断面形状でも一つ一つ分解していけばここまでで紹介した形状の組み合わせであることがほとんどだ。
組み合わせが分かればそれぞれのパーツの面積と断面2次モーメントがわかれば平行軸の定理で足したり引いたりすれば複雑な断面でも求められる。
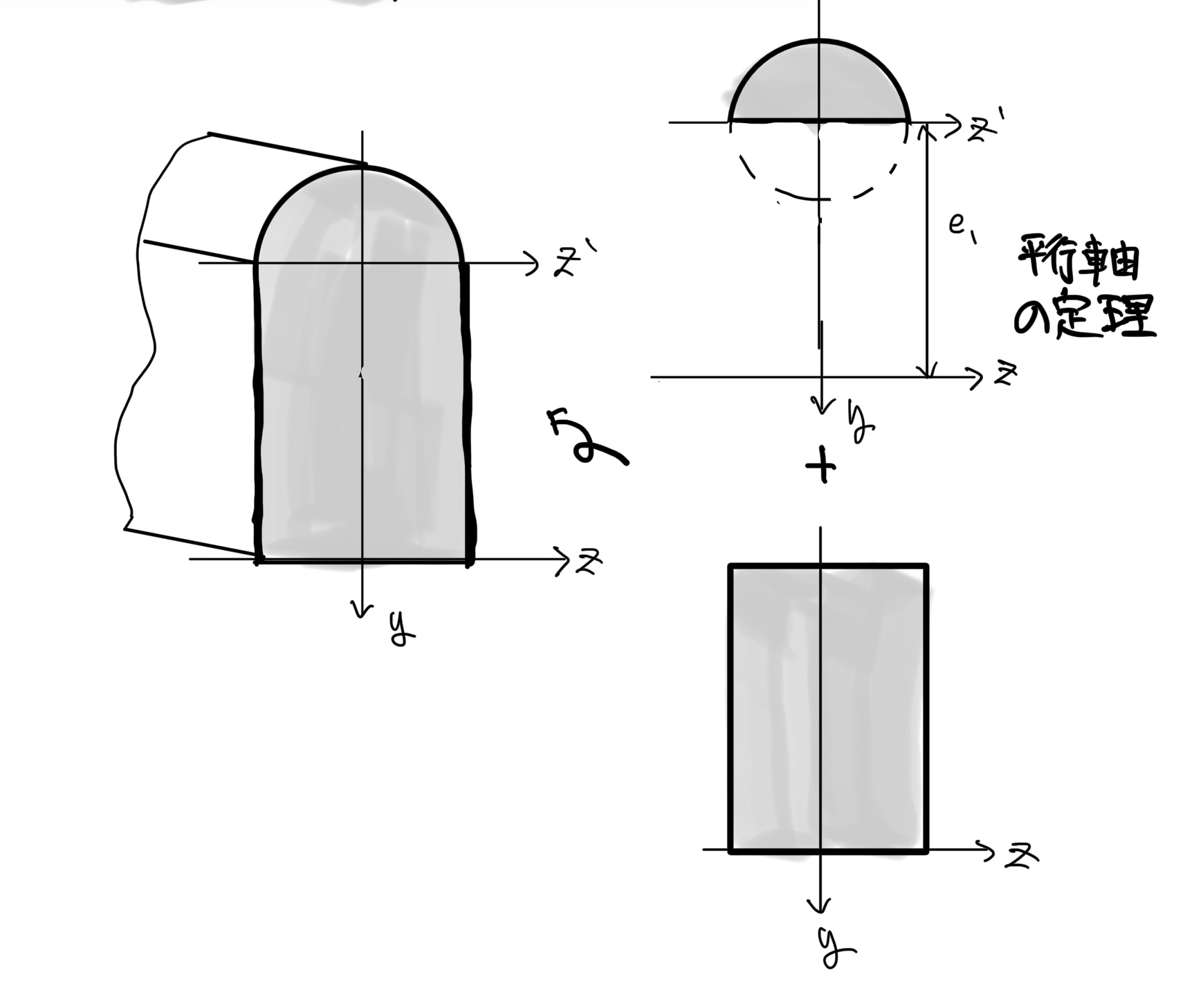
実際には図心を通る軸がはりの中立にならないことが多いが平行軸の定理を使えば簡単に求まる。
時間がある方や学生諸君は実際に平行軸の定理を使って自分で解いてみると理解が深まるはずだ。
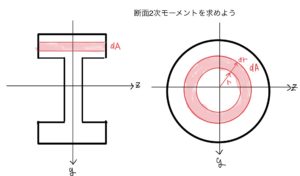
昨今ではシミレーションで求めてしまうことが多いと思うがレイアウトやスケッチ段階でどんな断面が良いのかは人間が判断するしかないので知っておいて損はない。
次回は、代表的なはりのたわみの早見表を紹介する。
この記事が「設計の理解」に少しでも役立ったと感じた方へ
基本的に本内容の教科書は存在せず筆者オリジナルですが筆者が学生から使っている教科書を紹介します。








コメント